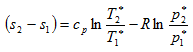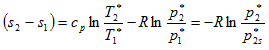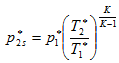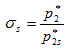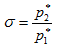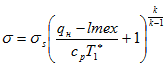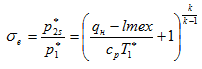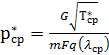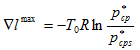К ВОПРОСУ ОБ ОСРЕДНЕНИИ ПАРАМЕТРОВ НЕОДНОМЕРНОГО ПОТОКА

Лепешинский И.А.

доктор технических наук, профессор, Московский авиационный институт (национальный исследовательский университет)

Работа выполнена при финансовой поддержки Минобрнауки РФ в рамках базовой части государственного задания

К ВОПРОСУ ОБ ОСРЕДНЕНИИ ПАРАМЕТРОВ НЕОДНОМЕРНОГО ПОТОКА

Аннотация

На основе закона Гюи-Стодолы рассматривается использование понятия эксергии для описания необратимых процессов. Получено выражение для потери эксергии записываемое через параметры торможения давления. Показано, что осреднение неравномерных потоков на основе выполнения законов сохранения массы, количества движения и энергии определяется величиной потерь эксергии.

Ключевые слова: осреднение неравномерных потоков, энтропия, эксергия, работоспособность, параметр необратимости процесса.

Lepeshinsky I.A.

PhD in Engineering, professor, Moscow Aviation Institute (National Research University) MAI, Moscow

ON THE AVERAGED PARAMETERS OF MULTIDIMENSIONAL FLOW

Abstract

On the basis of the law of Guy - Stodola it is explained how to use the concept of exergy to describe irreversible processes. An expression for exergy losses recorded through the parameters of the total pressure is received. It is shown that the averaging of  irregular flows based on the implementation of the laws of conservation of mass, momentum and energy is determined by the loss of exergy.

Keywords: averaging of non-uniform streams, entropy, exergy, working capacity, irreversibility parameter of process.

При решении практических газодинамических задач приходится рассчитывать газовые потоки с переменными по сечению параметрами. Такие потоки также реализуются в экспериментальных исследованиях. В ряде случаев проводят осреднение таких потоков, а для анализа полученных результатов используют средние значения параметров, полученные при осреднении. В этом случае приходится формулировать математические модели, в качестве которых используются модели элементарной струйки [1, 2, 3]. Эти модели позволяют достаточно хорошо описывать физику процесса. Для замыкания системы уравнений математической модели используется понятие энтропии. Играя значительную роль в развитии науки, это понятие по целому ряду причин  является весьма трудным и неудобным для практического использования, более подробно об этом можно прочитать, например, в [4]. Отметим только наиболее важные для нас недостатки энтропии. Энтропию нельзя измерить, что весьма важно при решении практических задач, она не позволяет  различать долю ее роста, связанную с внешним подогревом и внутренним трением в системе. Но самое главное, если в системе происходит необратимый процесс, то система уравнений математической модели замыкается неравенством для изменения энтропии Δs>0 или ds>0, т.е. констатируется только факт необратимости процесса, но система уравнений остается незамкнутой. Здесь s энтропия на единицу массы, Дж/кг×К. Это связано с тем, что в данном случае необходимо уметь вычислять производство энтропии [4]. Справедливости ради, следует сказать, что этим достаточно успешно занимается «Термодинамика необратимых процессов» [4, 5, 6,], однако получаемые там решения   не менее сложны, чем исходная газодинамическая задача.

Сформулированная проблема с энтропией может быть  решена путем использования понятия эксергии или работоспособности [7,8]. Эксергия или работоспособность-это максимальная работа, которую может совершить в обратимом процессе взаимодействия с окружающей средой система, если в конце этого процесса рабочее тело системы приходит в состояние равновесия со всеми параметрами окружающей среды. Различие в  химическом составе рабочих тел системы и окружающей среды здесь не рассматривается. Обозначим параметры окружающей среды индексом "0", тогда для газа его удельная полная энергия на уровне окружающей среды запишется как

                                                                                          (1),

энергия в состоянии "1" как

                                                                                          (2),

здесь c_р  удельная теплоемкость при постоянном давлении, Дж/кг×К, температура торможения в градусах Кельвина. Тогда удельная на единицу массы эксергия  в состоянии "1" будет

                                                            (3).

Изменение эксергии системы между двумя состояниями "1" и "2" запишется как

                                                         (4).

Потери эксергии от необратимости в  этом процессе запишутся как

                                                                               (5).

Формула (5) выражает закон Гюи-Стодолы [7] для потери эксергии или работоспособности. Эти потери характеризуют диссипацию энергии, т.е. показывают какая часть энергии, которая в целом сохраняется, теряет способность к совершению работы. Воспользуемся известным выражением [1, 2, 3] связывающим изменение энтропии с параметрами торможения газодинамической системы.

                                                                           (6),

здесь  давление торможения, н/м².

Можно показать [3], что последнее выражение преобразуется в

                                                  (7),

где

                                                                                (8),

k показатель изоэнтропы, а  давление торможения, полученное в изоэнтропическом процессе изменения состояния. Тогда потери эксергии   можно записать, как

                                                                             (9),

R удельная газовая постоянная, Дж/кг×К.

Будем полагать, что основными параметрами системы струйки являются p-давление, Т-температура, ρ- плотность, w-скорость, F-площадь сечения струйки. Поэтому для замкнутой математической модели необходимо иметь пять уравнений. Можно указать алгоритм построения такой модели [3]. Это три закона сохранения (массы, количества движения, энергии), определяющее уравнение. Поскольку законы сохранения не содержат никакой информации о рабочем теле, определяющим уравнением обычно является уравнение состояния. О пятом уравнении будет сказано ниже.

Из (9) следует, что увеличение энтропии или потери эксергии однозначно определяются давлением торможения, которое таким образом является эксергетическим параметром, т.е. характеризует эксергию системы.

Величину

                                                                                           (10).

назовем параметром необратимости процесса. Для энергетически изолированной системы, когда

                                                                    (12).

можно дать газодинамическую формулировку второго закона термодинамики, точнее одной из формулировок, называемой иногда принципом возрастания энтропии [8], которая звучит в термодинамике так:

энтропия изолированной системы возрастает (для необратимых процессов) или в пределе остается постоянной (для обратимых процессов). Газодинамическая формулировка, которую будем называть принципом уменьшения давления торможения, формулируется так:

В изолированной газодинамической системе давление торможения остается постоянным (в обратимых процессах) или уменьшается (в необратимых процессах).

Рассмотрим общий случай процесса в неизолированной системе между двумя состояниями "1" и "2". Обозначим изменение давления торможения для этого случая как

                                                                                             (13).

Воспользуемся уравнением энергии для элементарной струйки в газодинамической форме [1, 2, 3]

                                                                          (14),

здесь q_н  внешнее количество тепла единицы массы, Дж/кг, l_тех   техническая работа единицы массы, Дж/кг.

Выражая отношение температур из (14) и подставляя его в (8), после преобразований получим

                                                                      (15).

Обозначим величину

                                                                (16),

и назовем ее коэффициентом обмена энергией. По существу эта величина характеризует изменение эксергии, которое могло бы быть, если бы процесс изменения энергии был бы обратимым. Тогда

                                                                                        (17).

Таким образом, удается отделить проблему необратимости  от проблемы обмена энергией, и в частности, от обмена теплом.

Пятое замыкающее уравнение, уравнение качества процесса, поскольку оно представляет собой альтернативу между обратимым и необратимым процессами, и, таким образом, характеризует качество процесса. Остановимся на нем подробнее. Теперь это уравнение, как для обратимого так и необратимого процесса записывается в виде равенства (9) (в отличие от энтропии). Для обратимого процесса потери эксергии равны нулю, т.е

                                                                                          (18),

и система замыкается уравнением изоэнтропы. Для необратимого процесса величина потерь эксергии определяется (вместо энтропии) значением давления торможения в конце рассматриваемого процесса, т.е. величиной . Она может быть рассчитана по известным газодинамическим формулам или измерена экспериментально, поскольку давление торможения легко измеряется в отличие от энтропии. При этом качество процесса может быть выражено величиной  потерянной эксергии (потерянной полезной работы).

Обратимся теперь к проблеме осреднения неодномерных потоков, которая рассматривалась в работах [1,9,10]. Заменяя неодномерный поток одномерным, следует стремиться к тому, чтобы сохранить неизменными такие интегральные характеристики как расход, импульс и энергия. Наиболее распространенным является метод нахождения средних значений параметров р^*,Т^*, и λ при сохранении в исходном и осредненном потоке величин расхода газа G, полной энергии Е и импульса I. Рассмотрим такой способ осреднения [1]. Пусть в поперечном сечении известны (заданы или измерены) все необходимые параметры. Тогда расход газа равен

                                                     (19),

На основе законов сохранения энергии и расхода определяется среднее значение температуры торможения 

                                                                                                       (20).

Теплоемкость с_р и показатель изоэнтропы k полагаются постоянными.

На основе среднемассовой температуры торможения  определяется среднее значение критической скорости звука α_кр,ср

                                                                                   (21).

Среднее значение приведенной скорости потока находится из уравнения импульсов

                                                     (22).

И теперь из уравнения расхода по средним значениям   и λ_ср определяется среднее значение 

                                                                                 (23).

Рассмотрим другой способ осреднения, при котором значение давления торможения определяется из условия постоянства энтропии s. Обозначим это давление как . Воспользуемся выражением для этой величины полученным в [1,10]

                                        (24).

Величина  меньше .Теперь можно определить потери эксергии, используя формулу (9)

                                                                            (25).

Потери эксергии неравномерного потока объясняются следующим [1]:

 полученные значения параметров ,  и λ_ср равны соответствующим параметрам такого потока, который может образоваться при выравнивании за счет перемешивания исходного неоднородного потока в теплоизолированной трубе постоянного сечения без трения о стенки; при этом расход, импульс и полная энергия  также сохранят свое значение. Осреднение такого потока и будет соответствовать постоянству энтропии. Потери эксергии связаны с потерями на перемешивание потока.

Из вышесказанного следует вывод о том, что рассмотренные выше два способа осреднения не являются альтернативными, а должны использоваться одновременно, поскольку они позволяют определить действительную работоспособность осредняемого потока. Возможно, будет целесообразно ввести эксергетический КПД осредняемого потока η как

                                                                     (26).

Литература

1. Абрамович Г.Н. Прикладная газовая динамика в 2х ч. Ч. 1,2 Учеб. руководство для втузов. – 5-е изд., перераб. и доп. – М.: Наука. Гл. ред. Физ.-мат. лит. 1991. С. 600.
2. Сергель О.С. Прикладная гидрогазодинамика. М.: Машиностроение. 1981. С. 374.
3. Лепешинский И.А. Газодинамика одно- и двухфазных течений в реактивных двигателях. М.: Изд-во МАИ. 2003. С. 276.
4. Вейник А.И. Термодинамика. М.: Высшая школа. 1968.С. 463.
5. Де Гроот С. Мазур П. Неравновесная термодинамика. М.:Мир.1964. С.329.
6. Пригожин И. Введение в термодинамику необратимых процессов. М.: ИЛ.1960.С. 357.
7. Шаргут Я. Петела Р. Эксергия. М.: Энергия. 1968.С. 279.
8. Кириллин В.А. Сычев В.В. Шейндлин А. Е. Техническая термодинамика. М.: Энергия.1968. С. 472.
9. Седов Л.И. Черный Г.Г. Об осреднении неравномерных потоков газа в каналах. М.: Оборонгиз. Теор. гидромеханика, сб. статей №12, вып.4.

С.17-30.

10. Черкез А.Я. О некоторых особенностях осреднения параметров в сверхзвуковом газовом потоке. Изд.Академии наук СССР, ОТН, №4, 1962.

С. 23-28.

References

1. Abramovich G.N. Prikladnaja gazovaja dinamika. v 2h ch. Ch. 1,2 Ucheb. rukovodstvo: Dlja vtuzov. – 5-e izd., pererab. i dop. – M.: Nauka. Gl. red. Fiz.-mat. lit. 1991. 600 s.
2. Sergel' O.S. Prikladnaja gidrogazodinamika. M.: Mashinostroe¬nie. 1981. 374 s.
3. Lepeshinskij I.A. Gazodinamika odno- i dvuhfaznyh techenij v reaktivnyh dvigateljah. M.: Izd-vo MAI. 2003. 276 s.
4. Vejnik A.I. Termodinamika. Mn.: Vyshejsha shkola. 1968. 463s.
5. De Groot S. Mazur P. Neravnovesnaja termodinamika. M.:Mir.1964.329s.
6. Prigozhin I. Vvedenie v termodinamiku neobratimyh processov. M.: IL.1960.357s.
7. Shargut Ja. Petela R. Jeksergija. M.: Jenergija. 1968.279s.
8. Kirillin V.A. Sychev V.V. Shejndlin A. E. Tehnicheskaja termodinamika. M.: Jenergija.1968. 472s.
9. Sedov L.I.Chernyj G.G. Ob osrednenii neravnomernyh potokov gaza v kanalah. M.: Oborongiz. Teor. gidromehanika, sb. statej №12,vyp.4. str.17-30.
10. Cherkez A.Ja. O nekotoryh osobennostjah osrednenija parametrov v sverhzvukovom gazovom potoke. .Izv.Akademii nauk SSSR, OTN, №4, 1962. str.23-28.