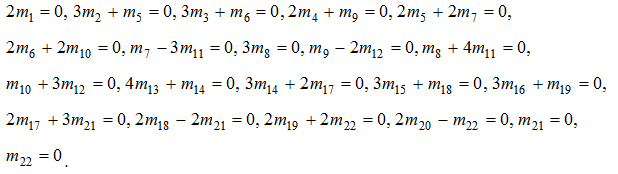ДОСТАТОЧНЫЕ УСЛОВИЯ НЕСТАБИЛЬНОСТИ ЭЛЕМЕНТА СВОБОДНЫХ НИЛЬПОТЕНТНЫХ ГРУПП
Ковыршина А.И.1, Лапшина Е.С.2
1Кандидат физико-математических наук, 2Кандидат физико-математических наук, Иркутский государственный университет
ДОСТАТОЧНЫЕ УСЛОВИЯ НЕСТАБИЛЬНОСТИ ЭЛЕМЕНТА СВОБОДНЫХ НИЛЬПОТЕНТНЫХ ГРУПП
Аннотация
Поиск стабильных элементов свободных нильпотентных групп тесно связан с нестабильными элементами в этих группах. При установлении достаточных условий существования нестабильных элементов значительно облегчается поиск стабильных. Статья посвящена описанию множества базисных коммутаторов определенного вида, среди линейных комбинаций которых нет стабильных элементов. Рассматривается свободная нильпотентная группа ранга 3 ступени 12.
Ключевые слова: автоморфизмы групп, неподвижные точки, нильпотентные группы.
Kovyrshina A.I.1, Lapshina E.S.2
1 PhD in Physics and Mathematics, 2 PhD in Physics and Mathematics, Irkutsk State University
SUFFICIENT CONDITIONS OF INSTABLE ELEMENTS OF FREE NILPOTENT GROUP
Abstract
Search of stable elements of free nilpotent groups is closely associated with unstable elements in these groups. In establishing sufficient conditions for the existence of unstable elements search for stability is much easier. The article describes the set of a particular type of basic commutators, among the linear combinations of which there are not stable elements. We consider the free nilpotent group of rank 3 class 12.
Keywords: automorphisms groups, fixed points, nilpotent groups.
Элемент ![]() группы
группы ![]() называется нестабильным, если существует автоморфизм
называется нестабильным, если существует автоморфизм ![]() , такой что
, такой что ![]()
Вопросами о существовании нетривиальных стабильных элементов в свободных нильпотентных группах занимались В.В. Блудов [1], А. Папистас [2], Е. Форманек [3], А.И. Ковыршина [4, 5]. Так, А. Папистас и Е. Форманек доказали существование нетривиальных стабильных элементов в свободных нильпотентных группах при определенных условиях на ступень и ранг группы. Работы [4, 5] посвящены описанию нетривиальных стабильных элементов свободных нильпотентных групп, ранг и ступень которых удовлетворяют условиям, найденным А. Папистас и Е. Форманек. Поиск стабильных элементов является технически сложным процессом. В работе [4] приведены основные теоремы, описывающие строение стабильных элементов группы ![]() - свободной нильпотентной группы ступени 12 ранга 3 с образующими
- свободной нильпотентной группы ступени 12 ранга 3 с образующими ![]()
![]()
![]() . Однако, вопрос о полном описании таких элементов в группе
. Однако, вопрос о полном описании таких элементов в группе![]() остался открытым.
остался открытым.
Нами доказана следующая теорема:
Теорема: Пусть ![]() - элемент группы
- элемент группы ![]() с образующими
с образующими ![]()
![]()
![]() . Если хотя бы один базисный коммутатор в разложении элемента
. Если хотя бы один базисный коммутатор в разложении элемента ![]() по базисным коммутаторам имеет вид
по базисным коммутаторам имеет вид ![]() , или
, или ![]() , где
, где ![]() ,
, ![]() , то
, то ![]() является нестабильным.
является нестабильным.
Доказательство. Нетрудно проверить, что среди линейных комбинаций элементов вида ![]() ,
, ![]() нет нетривиальных стабильных элементов. Покажем, что среди комбинаций базисных элементов вида
нет нетривиальных стабильных элементов. Покажем, что среди комбинаций базисных элементов вида ![]() их нет. Наибольший интерес представляет случай, когда
их нет. Наибольший интерес представляет случай, когда ![]() , так как базисный коммутатор вида
, так как базисный коммутатор вида ![]() под действием автоморфизмов, порождающих группу всех автоморфизмов группы
под действием автоморфизмов, порождающих группу всех автоморфизмов группы ![]() , становится небазисным.
, становится небазисным.
Введем следующие обозначения базисных коммутаторов вида ![]() :
:
Пусть ![]() - линейная комбинация элементов
- линейная комбинация элементов ![]() с целыми коэффициентами
с целыми коэффициентами ![]() . Подействуем на элемент
. Подействуем на элемент ![]() автоморфизмом
автоморфизмом ![]() ,
, ![]() . Линейная комбинация всех базисных коммутаторов, полученных из
. Линейная комбинация всех базисных коммутаторов, полученных из ![]() заменой одного вхождения образующего
заменой одного вхождения образующего ![]() на
на ![]() равна:
равна:
После приведения подобных, запишем условия, при которых рассматриваемая сумма равна нулю:
Далее, применим к элементу ![]() автоморфизм
автоморфизм ![]() ,
,![]() . Коммутатор
. Коммутатор ![]() входит в линейную комбинацию всех коммутаторов, полученных из
входит в линейную комбинацию всех коммутаторов, полученных из ![]() заменой одного вхождения образующего
заменой одного вхождения образующего ![]() на
на ![]() с коэффициентом
с коэффициентом ![]() . Приравняем данный коэффициент к нулю и решим систему полученных уравнений с учетом равенства
. Приравняем данный коэффициент к нулю и решим систему полученных уравнений с учетом равенства ![]() .
.
Объединенная система имеет единственное нулевое решение. Таким образом, при любых целых значениях ![]() элемент
элемент ![]() является нестабильным элементом.
является нестабильным элементом.
Пусть разложение элемента ![]() по базисным коммутаторам имеет вид
по базисным коммутаторам имеет вид ![]() , где
, где ![]() - линейные комбинации коммутаторов вида
- линейные комбинации коммутаторов вида ![]() ,
, ![]() - линейные комбинации коммутаторов вида
- линейные комбинации коммутаторов вида ![]() ,
, ![]() ,
, ![]() - линейная комбинация коммутаторов, вид которых отличен от вида коммутаторов, входящих в
- линейная комбинация коммутаторов, вид которых отличен от вида коммутаторов, входящих в ![]() и
и ![]() .
.
Рассмотрим ![]() , где
, где ![]() - коммутант группы
- коммутант группы ![]() . Множество
. Множество ![]() не содержит коммутаторов вида
не содержит коммутаторов вида ![]() , а все элементы вида
, а все элементы вида ![]() принадлежат
принадлежат ![]() . Так как
. Так как ![]() - характеристическая подгруппа, то для любого автоморфизма
- характеристическая подгруппа, то для любого автоморфизма ![]() в автоморфном образе базисных элементов вида
в автоморфном образе базисных элементов вида ![]() не может быть коммутаторов вида
не может быть коммутаторов вида ![]() . Среди линейных комбинаций элементов рассматриваемых видов нет нетривиальных стабильных элементов, поэтому существует автоморфизм
. Среди линейных комбинаций элементов рассматриваемых видов нет нетривиальных стабильных элементов, поэтому существует автоморфизм ![]() , такой что
, такой что ![]() . Подействуем автоморфизмом
. Подействуем автоморфизмом ![]() на
на ![]() .
.
Рассмотрим подгруппу ![]() . Элементы
. Элементы ![]() и
и ![]() не принадлежат
не принадлежат ![]() ,
,
а ![]() , так как
, так как ![]() - линейная комбинация коммутаторов, вид которых отличен от вида коммутаторов, входящих в
- линейная комбинация коммутаторов, вид которых отличен от вида коммутаторов, входящих в ![]() и
и ![]() . Так как
. Так как ![]() - характеристическая подгруппа, то для автоморфного образа элемента
- характеристическая подгруппа, то для автоморфного образа элемента ![]() выполняется условие
выполняется условие ![]() . Следовательно, коммутаторы вида
. Следовательно, коммутаторы вида ![]() или
или ![]() не входят в разложение
не входят в разложение ![]() . Таким образом,
. Таким образом, ![]() , в
, в ![]() нет элементов, входящих в
нет элементов, входящих в ![]() или
или ![]() , а значит
, а значит ![]() . Теорема доказана.
. Теорема доказана.
Литература
- Блудов В.В. Неподвижные точки относительно всех автоморфизмов в свободных нильпотентных группах. //Третий Сибирский конгресс по прикладной и индустриальной математике. Тез. докл. часть 5. Новосибирск, 1998.
- Papistas A. A note on fixed points of certain relatively free nilpotent groups //Communications in algebra. 2001. No. 29, Pp. 4693-4699.
- Formanek E. Fixed points and centers of automorphism groups of free nilpotent groups // Communications in algebra. 2002. No. 30. Pp. 1033-1038.
- Ковыршина А.И. Стабильные элементы в свободных нильпотентных группах ранга три // Вестник Омского университета. – 2010. – №4 (58). – С. 20–23.
- Ковыршина А.И. О стабильных элементах в свободных нильпотентных группах ранга два // Вестник Бурятского государственного университета. Серия: Математика и информатика. – 2015. – № 9. – С. 3–6.
References
- Bludov V.V. Fixed points with respect to all automorphisms in free nilpotent groups // Third Siberian Congress on Industrial and Applied Mathematics. Proc. rep. Part 5. Novosibirsk. 1998. 2. Papistas A. A note on fixed points of certain relatively free nilpotent groups //Communications in algebra. 2001. No. 29, Pp. 4693-4699.
- Formanek E. Fixed points and centers of automorphism groups of free nilpotent groups // Communications in algebra. 2002. No. 30. Pp. 1033-1038.
- Kovyrshina A.I. Fixed points with respect to all automorphisms of the free nilpotent groups for three generators // Herald of Omsk University. 2010. No. 4 (58). Pp. 20-23.
- Kovyrshina A.I. Stable elements in free nilpotent groups of rank two // Bulletin of Buryat State University. – 2015. – No.9. – Pp. 3–6.