АНАЛИЗ ДИНАМИКИ ПРОБИТИЯ ПРЕГРАД КОМПАКТНЫМИ УДАРНИКАМИ

Глазырин В.П.¹, Орлов Ю.Н.²

¹Доктор физико - математических наук, ²кандидат физико-математических наук, Национальный исследовательский Томский государственный университет

Работа выполнена при финансовой поддержке Минобрнауки РФ в рамках государственного задания №2014/223 (код проекта 1567)

АНАЛИЗ ДИНАМИКИ ПРОБИТИЯ ПРЕГРАД КОМПАКТНЫМИ УДАРНИКАМИ

Аннотация

При помощи методов математического моделирования исследован процесс взаимодействия компактных ударников с алюминиевыми преградами. Рассмотрены сферические и цилиндрические  ударники.  Поведение среды описывается с общих позиций механики деформируемого твердого тела. Учитываются ударно-волновые явления, а также образование отрывных и сдвиговых разрушений. Для численного моделирования процесса соударения тел использована разработанная методика. Рассмотрен двумерный случай осевой симметрии. Получены текущие конфигурации ударник-мишень, области разрушенного материала и временные  параметры моделируемого процесса.

Ключевые слова: модель, скорость, ударник, преграда, метод, пробитие.

Glazyrin V.P.¹, Orlov Y.N.²

¹Doctor of Physical - Mathematical Sciences, ²Candidate of Physical-Mathematical Sciences, National  Research Tomsk State University

ANALYSIS OF DYNAMICS PENETRATING OF TARGETS BY COMPACT STRIKERS

Abstract

With the help of mathematical modeling methods used to study the interaction of compact strikers aluminum targets. Consider a spherical and cylindrical strikers. The behavior of the medium is described by the general position of solid mechanics. Taking into account the shock-wave phenomena, as well as education vouchers and shear damage. For the numerical simulation of the collision of bodies used the method developed. Considered two-dimensional case of axial symmetry. Get current configuration strikers - target, the area of ​​damaged material and temporal parameters of the modeled process.

Keywords: model, velocity, striker, target, method, penetration.  

В практике создания ударостойких защит часто применяют инженерные формулы, позволяющие, не прибегая к анализу сложного напряженно-деформированного состояния, оценивать надежность преграды. В большинстве таких формул, используется величина предела сквозного пробития или баллистический предел. Поэтому более точное знание запреградной скорости ударника V_з   предполагает и более точные расчеты по таким формулам. Очевидно, что результаты экспериментов по определению данных величин зависят от разных факторов, возможно, в том числе, и от фронтальных размеров преграды. Это актуально, поскольку материалы для современных ударостойких защит на этапе их разработки стоят довольно дорого, а образцы, как правило, невелики по размерам.

С целью проверки влияния размера преград на значение запреградной скорости ударника проведены расчеты взаимодействия стальных ударников сферической и цилиндрической формы одинаковой массы диаметром 15 мм с плитами из алюминиевого сплава Д16 толщиной 4 мм с динамическим пределом текучести 0.5 ГПа. Преграды расположены на опорных кольцах с внутренним диаметром 9.0 и 2.5 см.  Начальная скорость ударников равна 290 м/с.

Для описания поведения материала используется модель упругопластической повреждаемой среды с упрочнением. Материал считается изотропным, упругопластическим, сжимаемым, пористым [1, 2]. Задача решается численно в осесимметричной постановке методом Джонсона, который дополнен алгоритмами разрушения расчетных элементов и расщепления расчетных узлов, позволяющими моделировать глубокое проникание ударников и сквозное пробитие преград с учетом разрушения тел на фрагменты [3, 4].

Микроповреждения в материале  трактуются как эволюционирующие в волнах напряжений микропустоты и описываются кинетическим уравнением порообразования [3, 4]. Принято, что отрывные разрушения происходят при достижении главным растягивающим напряжением значения откольной прочности, а сдвиговые разрушения – при достижении удельной работой сдвиговых пластических деформаций критического значения [5].

Начальная схема моделируемого процесса приведена на рис. 1а. На рис. 1б представлены результаты расчетов процесса взаимодействия сферического ударника с алюминиевой плитой, расположенной на большом кольце. Наблюдается сквозное пробитие, а V_з=153 м/с. Изменение относительной скорости центра масс ударника приведено на рис. 2 (кривая 1c). Отсюда видно, что пробитие преграды происходит приблизительно на 90 мкс процесса. На рис. 1в и рис. 1г приведены результаты расчета для случая, когда преграда лежит  на опорном кольце меньшего диаметра. Изменение относительной скорости центра масс ударника приведено на рис. 2 (кривая 2с). Сквозное пробитие наблюдается на 50 мкс процесса, а V_з=167 м/с.

Для выяснения влияния формы головной части проведены расчеты по моделированию процесса взаимодействия цилиндрического ударника с такой же преградой. Результаты расчета представлены на рис. 3. Изменение относительной скорости центра масс для этих вариантов приведены на рис. 2 (кривые 1ц и 2ц). Запреградная скорость цилиндра при пробитии преграды на большом кольце равна 192 м/с и на малом - 203 м/с.

 

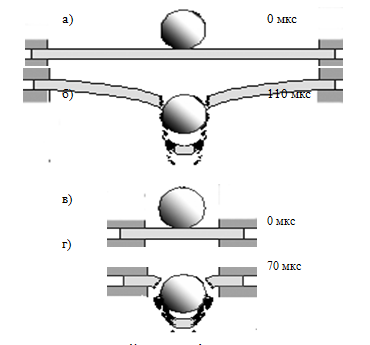
Рис. 1 - Взаимодействие сферического ударника с преградой

 

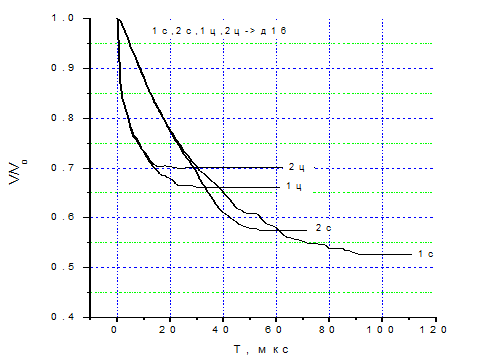
Рис. 2 - Зависимость  скорости центра масс ударников от времени

 

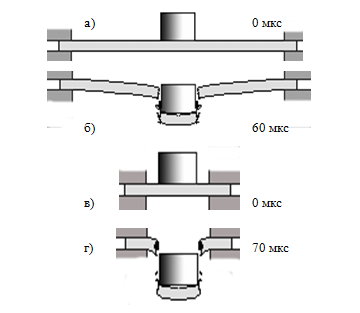
Рис. 3 - Взаимодействие цилиндрического ударника с преградой

 

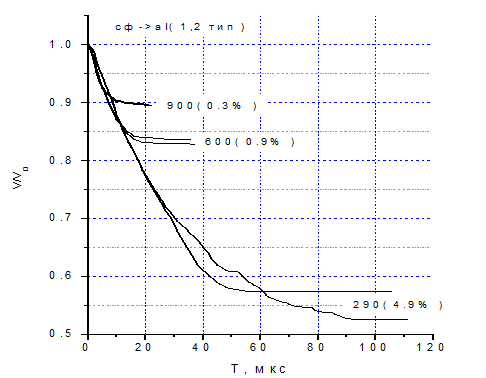
Рис. 4 - Зависимость  скорости центра масс ударников от времени при различных начальных скоростях удара

 

Обозначим преграду большего диаметра как тип 1, а преграду меньшего диаметра - как тип 2. Из расчетов следует, что после пробития преграды первого типа сферическим ударником, его относительная V_з равна 0.53, а после пробития преграды второго типа – 0.57, т.е. разница между ними составила 14 м/с. Относительные V_з цилиндрического ударника для аналогичных вариантов расчетов дают 0.66 и 0.71 с разницей в 11 м/с.

Запреградные скорости ударников в случае преград типа 1 ниже, чем в случае преград типа 2 видимо из-за того, что в первом случае деформируется больший объем материала, чем во втором, т.е. в первом случае тратится больше кинетической энергии ударника на упругопластическое деформирование преграды, чем во втором.

На рис. 4 приведены графики относительной скорости сферического ударника при пробитии преград 1 и 2 типа при начальных скоростях 290, 600 и 900 м/с. Напротив кривых указаны начальные скорости, а в скобках – процентная разница запреградных скоростей при пробитии преград разного типа. Видно, что с увеличением начальной скорости разница уменьшается. Это можно объяснить тем, что при высоких скоростях инерционная масса играет роль упора, и влияние размеров преград снижается.

В результате проведенных расчетов установлена степень влияния размера преград на значение запреградных скоростей сферических и цилиндрических ударников. Численные исследования позволили дать сравнительную оценку пробивного действия ударников различной формы и, кроме того, показали возможность применения и перспективность разработанного программного комплекса к решению задач сквозного пробития преград. Полученные данные нельзя автоматически распространять на любые другие материалы, размеры и скорости. Для решения такой задачи требуются проведение дополнительных исследований и экспериментальная проверка результатов.

Литература

1. Герасимов А.В., Пашков С.В. Взаимодействие высокоскоростных элементов с комбинированными преградами // Известия вузов. Физика. – 2011. - т. 54, № 10/2. - С. 25-29.
2. Глазырин В.П., Платова Т.М. О релаксации напряжения сдвига в металлах при ударном нагружении // Журнал Физика горения и взрыва. – 1988. - №1. – С. 79-83.
3. Орлов Ю.Н., Глазырин В.П., Орлов М.Ю. Удар-ПЛ-2. Разрушение тел при соударении. Плоская задача. Свидетельство о государственной регистрации программы для ЭВМ № 2010610912 от 21.01.2010.
4. Глазырин В.П., Орлов М.Ю., Орлов Ю.Н. Моделирование ударно-волнового нагружения функционально-градиентных материалов  // Известия вузов. Физика. – 2007. - т. 50, № 9/2. - С. 65-73.
5. Герасимов А.В., Пашков С.В. Численное моделирование пробития слоистых преград// Механика композиционных материалов и конструкций // Механика композиционных материалов и конструкций. – 2013. - т.19, №1. - С. 48-61.

References

1. Gerasimov A.V., Pashkov S.V. Vzaimodejstvie vysokoskorostnyh jelementov s kombinirovannymi pregradami // Izvestija vuzov. Fizika. – 2011. - t. 54, № 10/2. - S. 25-29.
2. Glazyrin V.P., Platova T.M. O relaksacii naprjazhenija sdviga v metallah pri udarnom nagruzhenii // Zhurnal Fizika gorenija i vzryva. – 1988. - №1. – S. 79-83.
3. Orlov Ju.N., Glazyrin V.P., Orlov M.Ju. Udar-PL-2. Razrushenie tel pri soudarenii. Ploskaja zadacha. Svidetel'stvo o gosudarstvennoj registracii programmy dlja JeVM № 2010610912 ot 21.01.2010.
4. Glazyrin V.P., Orlov M.Ju., Orlov Ju.N. Modelirovanie udarno-volnovogo nagruzhenija funkcional'no-gradientnyh materialov // Izvestija vuzov. Fizika. – 2007. - t. 50, № 9/2. - S. 65-73.
5. Gerasimov A.V., Pashkov S.V. Chislennoe modelirovanie probitija sloistyh pregrad// Mehanika kompozicionnyh materialov i konstrukcij // Mehanika kompozicionnyh materialov i konstrukcij. – 2013. - t.19, №1. - S. 48-61.