ОЦЕНКА ВЕРХНЕЙ ГРАНИЦЫ ВЕРОЯТНЫХ ЗНАЧЕНИЙ ФАЗОВОЙ СКОРОСТИ ВОЛН ДЕ БРОЙЛЯ
Попов И.П.
Курганский государственный университет
ОЦЕНКА ВЕРХНЕЙ ГРАНИЦЫ ВЕРОЯТНЫХ ЗНАЧЕНИЙ ФАЗОВОЙ СКОРОСТИ ВОЛН ДЕ БРОЙЛЯ
Аннотация
Показано, что эксперименты по интерференции и дифракции единичных частиц позволяют оценить верхнюю границу вероятных значений фазовой скорости волн де Бройля. При этом установлено, что фазовая скорость не может быть больше скорости частицы.
Ключевые слова: интерференция, дифракция, фазовая скорость, волны де Бройля.
Popov I.P.
Kurgan State University
UPPER BOUND PROBABILITY OF THE VALUE OF THE PHASE VELOCITY OF THE DE BROGLIE
Abstract
It is shown that experiments on interference and diffraction of single particles allow us to estimate the upper limit of possible values of the phase velocity of de Broglie waves. It was found that the phase velocity can not be greater than the velocity of the particle.
Keywords: interference, diffraction, phase velocity, the de Broglie wavelength.
Фазовая скорость волн де Бройля считается принципиально не наблюдаемой величиной [1]. Этим отчасти объясняется наличие в литературе ее двух существенно отличающихся друг от друга значений:
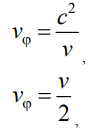 (1)
(1)
где c – скорость света, v – скорость частицы [1]. Первое выражение получено при обобщении формулы для волновой энергии на полную энергию частицы, а второе – на кинетическую [2–5]. Непосредственно измерить фазовую скорость не представляется возможным. Однако эксперименты по интерференции и дифракции единичных частиц позволяют оценить верхнюю границу ее вероятных значений.
Пусть фазовая скорость волн де Бройля для инертной частицы удовлетворяет выражению (1). Это означает, что фазовая скорость в любом случае больше скорости частицы. Поэтому любая фаза волны опережает частицу.
Пусть в момент t0 = 0 единичная частица проходит через одну из щелей устройства для наблюдения интерференции частиц. Пусть в этот же момент времени задний фронт части волны де Бройля проходит через другую щель. Этот задний фронт, распространяющийся с фазовой скоростью, достигнет детектора в момент t1
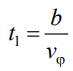 ,
,
где b – расстояние до детектора. Интерференционная картина закончится в момент t1, не позднее.
Частица достигнет детектора в момент t2
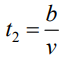 .
.
Поскольку в соответствии с (1) скорость частицы меньше фазовой скорости, частица окажется в детекторе тогда, когда интерференционная картина уже закончилась. Поэтому местоположение частицы не будет подчиняться распределению плотности вероятности, которого уже нет.
Таким образом, условие (1) несовместимо с возможностью возникновения интерференционной картины от единичных частиц.
Приведенные рассуждения в равной мере справедливы для дифракции единичных частиц на кристаллах.
Факты возникновения интерференционной и дифракционной картины от единичных частиц установлены экспериментально. Следовательно, из этих экспериментов очевидным образом следует соотношение
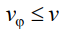 .
.
Список литературы
Сивухин Д.В. Общий курс физики. Т. 5. Атомная и ядерная физика. М.: ФИЗМАТЛИТ; Изд-во МФТИ. 2002. 784 с.
Попов И.П. Об одном проявлении инертности // Естественные и технические науки. 2013. № 1(63). С. 23–24.
Попов И.П. О влиянии инертности частицы на ее волновое представление // Вестник Забайкальского государственного университета. 2013. № 04(95). С. 90–94.
Попов И.П. Корпускулярный и волновой походы к теории эффекта Комптона // Естественные и технические науки. 2013. № 1(63). С. 41– 43.
Попов И.П. О волновой энергии инертной частицы // Зауральский научный вестник. 2013. № 1(3). С. 60–61.
