ТЕОРИЯ И ПРАКТИКА ИДЕНТИФИКАЦИИ ПАРАМЕТРОВ ТОНКОПЛЕНОЧНЫХ МАГНИТОЧУВСТВИТЕЛЬНЫХ СЕРДЕЧНИКОВ

Власкин К.И.¹, Прищепов С.К.²

¹Младший научный сотрудник, Уфимский государственный авиационный технический университет; ²кандидат технических наук, доцент, Уфимский государственный авиационный технический университет

ТЕОРИЯ И ПРАКТИКА ИДЕНТИФИКАЦИИ ПАРАМЕТРОВ ТОНКОПЛЕНОЧНЫХ МАГНИТОЧУВСТВИТЕЛЬНЫХ СЕРДЕЧНИКОВ

Аннотация

Определены условия задачи идентификации параметров магниточувствительных сердечников стержневых дифференциальных феррозондов. Произведены анализ и классификация параметров тонкопленочных аморфных сплавов, как исходных материалов стержневых магниточувствительных сердечников, составляющих основу их метрологической аттестации. Разработана математическая модель идентификации магнитных параметров стержневых тонкопленочных сердечников; представлены результаты их лабораторных исследований.

Ключевые слова: дифференциальный стержневой феррозонд; магниточувствительные сердечники; тонкопленочные аморфные сплавы; диаграмма направленности феррозонда.

Vlaskin K.I. ¹, Prischepov S.K. ²

¹ Junior research associate, Ufa State Aviation Technical University; ² PhD in technical sciences, associate professor, Ufa State University; Ufa State Aviation Technical University

THEORY AND PRACTICE OF THE THIN-FILM MAGNETIC CORES PARAMETRS IDENTIFICATION

Abstract

The problem of the thin-film magnetic cores differential rod-shaped fluxgate sensor parameters identification is identified. Analysis and classification of the parameters of the thin-film amorphous alloys, which form the basis of metrological attestation, are produced. The mathematical model of magnetic parameters of rod-shaped thin-film amorphous alloys is developed. The laboratory findings are presented.

Keywords:  differential rod-shaped fluxgate sensor; magnetic core; thin-film amorphous alloys; fluxgate pattern.

К наиболее эффективным средствам прецизионных измерений магнитных величин относятся в настоящее время первичные преобразователи феррозондового (ФЗ) типа. ФЗ-датчики характеризуются: высокими чувствительностью и быстродействием, малыми габаритами и энергоемкостью, острой диаграммой направленности. Данная совокупность характеристик ФЗ позволяет получать малые погрешности измерений вне зависимости от характера контролируемого магнитного воздействия: скалярного, векторного или тензорного.

Дифференциальный стержневой феррозонд (ДСФ) классического исполнения имеет конструкцию с параллельными полуэлементами (Рис.1, а). Недостатком данной конструкции является необходимость строгой идентификации параметров двух магниточувствительных сердечников. В конструкции по Рис.1, б полуэлементы ДСФ расположены соосно, что способствует совмещению его геометрической оси с физической осью чувствительности  (ОЧ) датчика. При этом магнитопровод может состоять из двух идентичных стержней или быть общим для полуэлементов ДСФ. 

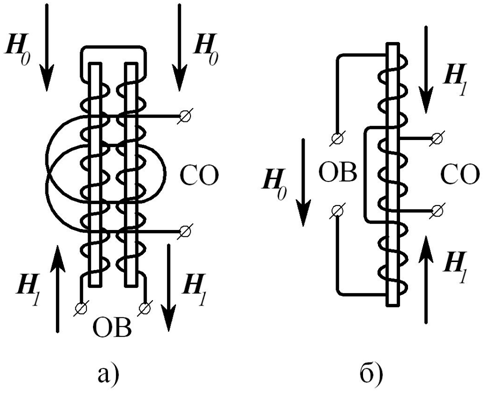
Рис.1. Функциональные схемы ДСФ. ОВ – обмотка возбуждения ФЗ; СО – сигнальная обмотка ФЗ; H₀ – измеряемое магнитное воздействие; H₁ – поле возбуждения.

Задача идентификации параметров магниточувствительных сердечников усложняется тем, что распространяется как на геометрические, так и на физические характеристики магнитопроводов. В настоящее время в качестве материалов магнитопроводов ДСФ применяются аморфные сплавы, обеспечивающие заданные метрологические и эксплуатационные характеристики датчиков. Аморфные сплавы производятся в виде лент со строго нормированной толщиной 20÷30 мкм и шириной 5÷60 мм. При этом технологически обеспечивается идентичность магнитных свойств аморфного сплава по всей длине и ширине ленты. Ширина изготавливаемых из лент магниточувствительных сердечников 0.3÷2.5 мм является для феррозондов расчетной величиной, так как определяет их параметры возбуждения, чувствительность и диаграмму направленности. Соотношение ширины и толщины сердечника представляет его как тонкопленочную структуру, поэтому ФЗ с такими сердечниками относятся к магнитометрическим датчикам с плоскими магнитными пленками (ПМП) [1].

Следовательно, с учетом однородности исходного магнитного материала по ширине и длине ленты, стержневой ПМП сердечник, для идентификации его параметров, можно представить в виде плоской фигуры с определенными размерами a, b, l, как по Рис.2.

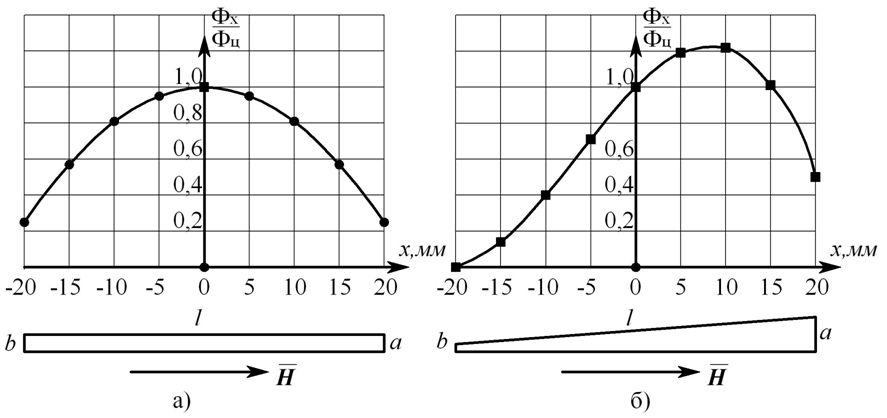
Рис.2. Распределение магнитных параметров по длине сердечника.

а) график при а=b; б) график при a > b; а, b – ширина сердечника на противоположных его краях; l – длина сердечника; Ф_ц – магнитный поток в центральном х=0 сечении сердечника; H – однородное магнитное поле.

График рис.2, а отражает приведенную в [2,3] математическую модель распределения по длине l магнитных параметров B; Ф в равномерном a=b стержневом сердечнике, помещенном в однородное магнитное поле H:

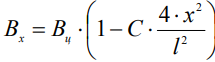,                                                     (1)

где B_x – значение магнитной индукции в сечении, расположенном на расстоянии х от центра х=0; B_ц – значение магнитной индукции в центральном сечении; С – постоянный коэффициент, зависящий от формы сердечника.

С учетом площади поперечного сечения сердечника S(x), из (1) следует:

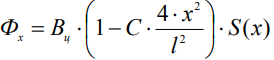,                                                (2)

где Ф_х – магнитный поток через S(x).

Для сердечника прямоугольной а=b формы  S(x) равна площади центрального х = 0 сечения сердечника S_ц  :  S(x) = S_ц . Тогда при   х=0;   Ф_х = const:

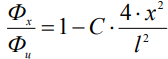,                                                         (3)

Для сердечника трапецеидальной формы a≠b площадь поперечного сечения зависит от координаты х :

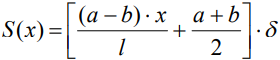,                                                (4)

где δ – толщина ПМП сердечника; a>b соотношение размеров сердечника, согласно Рис.2, б.

С учетом формул (2) и (4) :

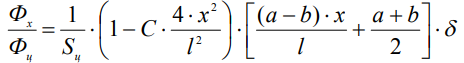,                          (5)

В общем случае a≠b и S_ц  в (5) определяется:

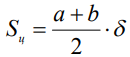.                                                              (6)

Подставляя (6) в (5) получаем:

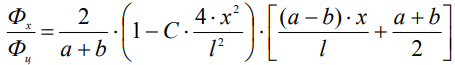.                             (7)

Характер распределения магнитных параметров, согласно формулам (3), (7) представлен на Рис.2.

Полученные в (2) – (7) функциональные зависимости позволяют определить магнитные параметры полуэлементов 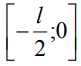 и 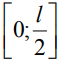 сердечника ДСФ. Средний магнитный поток Ф_ср  трапецеидального ПМП сердечника определяется:

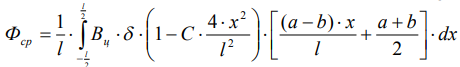,                            (8)

где 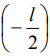  соответствует х= –20  мм;  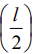соответствует х=20  мм (Рис.2).

Из (8) определяются средние магнитные потоки полуэлементов Ф_ср1 и Ф_ср2 :

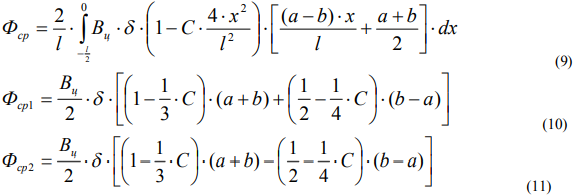
Из формул (10) и (11) следует, что равенство магнитных потоков Ф_ср1 = Ф_{ср2 ,} обеспечивающее баланс дифференциального ФЗ, выполняется в ДСФ с сердечниками прямоугольной формы  а=b (Рис.2).

С целью определения адекватности математических моделей (7), (10), (11) полученных для ПМП трапецеидальной формы, были проведены экспериментальные исследования распределения магнитных параметров по длине l=40 мм тонкопленочных δ=30 мкм сердечников с заданными а=2 мм, b=0,1 мм. Исследования проводились двумя независимыми методами: феррозондовым и измерения индуктивности. Графики Рис.3 свидетельствуют о сходимости результатов независимых измерений, что подтверждает их достоверность, а также соответствие данных эксперимента – теоретическим (Рис.2).

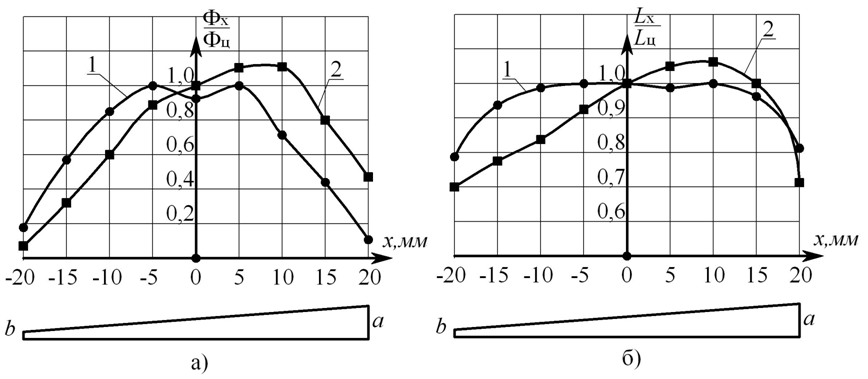
Рис.3. Результаты измерений магнитных параметров сердечников.

а) феррозондовый метод; б) метод измерения индуктивности.

 1 – график при а=b; 2- график при а>b.

Заключительный этап экспериментальных исследований был проведен по классической методике [2] для определения влияния неравномерности а>b сердечника по его длине l на диаграмму направленности одностержневого ДСФ конструкции Рис.1,б в однородном магнитном поле Земли H.

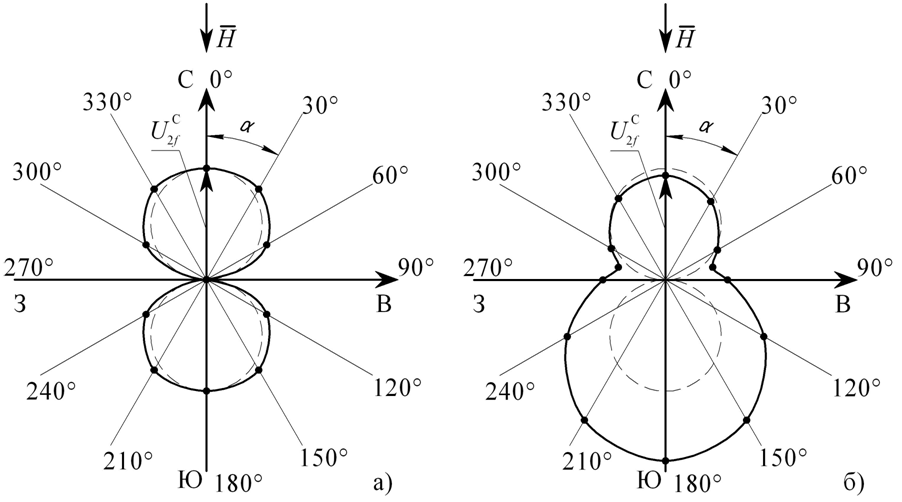
Рис.4. Диаграммы направленности ДСФ с трапецеидальным сердечником.

С, Ю, З, В – географические координаты; H – вектор магнитного поля Земли; U_2f – информационный сигнал ФЗ; U^С_2f  – U_2f при ОЧ ФЗ || H ; α – угол между ОЧ ФЗ и H ; а) диаграмма при а=b по Рис.2,а – основная линия; диаграмма «идеального» ДСФ – пунктир; б) диаграмма при а>b по Рис.2,б – основная линия; диаграмма «идеального» ДСФ – пунктир.

Выводы:

1. С учетом однородности исходного материала, для идентификации магнитных параметров стержневых ПМП сердечников, справедливо представлять их в виде плоской трапецеидальной фигуры (Рис.2) с определенными a,b,l – параметрами.

2. Распределение магнитных свойств по l – длине трапецеидального стержневого сердечника относительно его центра адекватно представляется математической моделью, содержащей геометрические параметры полуэлементов ,  .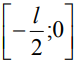

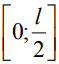3. При использовании ПМП сердечников трапецеидальной a,b,l – формы (Рис.2), условием баланса одностержневого ДСФ (Рис.1,б), обеспечивающего в частности, близкую к «идеальной» диаграмму направленности (Рис.4,а) является равенство сторон трапеции а=b.