СПОСОБ ОПРЕДЕЛЕНИЯ ЭКВИВАЛЕНТНОГО ДИАМЕТРА ПО ДИСПЕРСНЫХ МАТЕРИАЛОВ

Костиков Е.С.¹, Мясников В.М.², Лобаев А.Н.³, Краснов Ю.В.²

¹Кандидат технических наук, ОАО «НИИК»; ²кандидат технических наук, доцент, Нижегородский государственный технический университет им. Р. Е. Алексеева; ³кандидат физико-математических наук, доцент, Нижегородский государственный технический университет им. Р. Е. Алексеева

СПОСОБ ОПРЕДЕЛЕНИЯ ЭКВИВАЛЕНТНОГО ДИАМЕТРА ПО ДИСПЕРСНЫХ МАТЕРИАЛОВ

Аннотация

В статье рассмотрен способ экспериментального определения эквивалентного диаметра пор. Способ разработан в рамках исследования нового вакуумно-камерного способа течеискания с пористыми мембранами. Результаты данного исследования могут быть использованы также при разработке и исследовании технических материалов и катализаторов с микропористой структурой.

Ключевые слова: порометрия, пористые материалы, вакуумные измерения.

Kostikov E. S.¹, Myasnikov V. M.², Lobaev A. N.³, Krasnov Y. V.²

¹Candidate of Engineering Sciences, JSC «NIIK»;²Candidate of Engineering Sciences, Associate Professor, Nizhny Novgorod State Technical University n. a. R. E. Alekseev; ³Candidate of Physical and Mathematical Sciences, Associate Professor, Nizhny Novgorod State Technical University n. a. R. E. Alekseev

METHOD OF DETERMINATION OF THE EQUIVALENT PORE DIAMETER OF DISPERSED MATERIALS

Abstract

In the article the method of experimental determination of the equivalent pore diameter. The method was developed during the research of a new vacuum-chamber method leak detection with the porous membranes. The results of this study can be used in the development and study of technical materials and catalysts with microporous structure.

Keywords: porometry, porous materials, vacuum measurement.

В современной химической промышленности применяется большое количество высокотоксичных соединений как в виде сырья и полупродуктов, так и в виде конечных продуктов технологического процесса. В крупнотоннажных производства данные вещества хранятся и транспортируются в больших объемах. Неотъемлемой частью экологической безопасности таких производств является проблема герметичности крупногабаритного технологического оборудования и трубопроводов. Надлежащий контроль герметичности (как первичный, так и периодический) регламентируется соответствующими нормативными документами.

Для проведения испытаний на герметичность разработано большое количество методов и способов, позволяющих не только определять суммарную негерметичность объекта контроля, но и указать место течи, то есть локализовать ее. В современном неразрушающем контроле намечена тенденция — разработка автоматизированных установок контроля герметичности и локализации течей.

В практике течеискания из газовых методов получили распространение пузырьковый и его модификация — вакуумно-пузырьковый способы [1]. Однако, они обладают рядом недостатков, которые не позволяют их использовать в условиях современного производства. Это и высокая трудоемкость контроля и низкая производительность труда, связанные с большим количеством вспомогательных операций; и необъективность результатов контроля, основанного на субъективном мнении оператора, и т. д. Всё это делает указанные способы малопригодными для реализации в автоматизированных установках контроля герметичности.

Для устранения приведенных выше недостатков был разработан вакуумно-камерный способ локализации течей с пористыми мембранами. Уст­ройство, реализующее данный способ [2], представляет собой накладную вакуумную камеру, устанавливаемую на контролируемую поверхность. Внутри камеры расположен датчик утечки пробного газа (ПГ), состоящий из пористой мембраны с газонепроницаемой верхней гранью и датчика по теплопроводности. Пористая мембрана служит для накопления утечки пробного газа, а также для защиты концентрационного поля от влияния окружающей среды.

Для исследования процессов, протекающих в устройстве локализации течи, на основе квазигомогенного приближения получена математическая модель нестационарной диффузии для случая передвижения пористой среды над покоящейся течью. Принцип квазигомогенного приближения заключается в отождествлении процессов, протекающих в сплошной среде, с процессами, протекающими в пористой среде в режиме свободно-молекулярного движения, но с введением эффективных параметров, определяемых экспериментально [3]. Для массопереноса ПГ в пористой среде в условиях вакуумных испытаний определяющим фактором является эффективный коэффициент диффузии, который, помимо всего прочего, зависит от порометрических свойств (диаметр пор и извилистость порового канала) пористой среды.

Так как для изготовления пористой мембраны используются тканные или эластичные полимерные материалы, то распространенные методы порометрии такие, как метод вдавливания ртути, или метод вытеснения жидкости, не могут быть здесь применены из-за деформации остова и набухания применяемых материалов в процессе порометрических измерений [4].

В связи с этим был разработан новый способ экспериментального опре­деления эквивалентного диаметра пор в макропористых материалах (с диаметром пор порядка 50 мкм) [5].

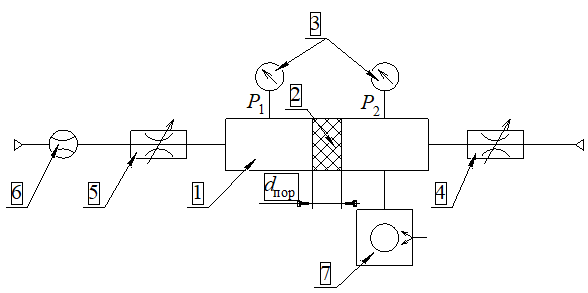
Установка, реализующая данный способ, показана на рис. 1. Она состоит из стеклянной трубки 1, в которую помещен слой пористого материала 2 (в условиях эксперимента использовался слой стекловаты толщиной d_пор). С двух концов к трубке подключены регулируемые дроссели 4, 5 и вакуумметры 3 типа 13ВТ3-003. Один из дросселей 5 соединен с капилляром 6, служащим для определения расхода воздуха Q, поступающим в трубку 1. Для откачки системы используется вакуумный насос 7 типа 2НВР-5ДМ.

Рис. 1 — Установка для определения эффективного диаметра пор

Напуском воздуха через регулируемые дроссели 4 и 5 можно устанавливать величину остаточного давления в вакуумной системе, создавая тем самым различные режимы течения газа через пористую среду.

Рассмотрим механизм определения эквивалентного диаметра пор, который основан на результатах молекулярно-кинетической теории. Известно, что между свободно-молекулярным (массоперенос за счет кнудсеновской диффузии) и вязкостным течением (массоперенос за счет молекулярной диффузии) существует переходная зона, в которой число Кнудсена 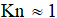, или, что тоже самое, 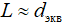, где L — длина свободного пробега молекулы ПГ,  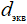— эквивалентный диаметр пор.

Для определения области переходного течения, воспользуемся тем фактом, что в условиях молекулярного течения по закону Кнудсена (для изотерического течения):

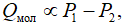         (1) а для вязкостного течения по закону Хагена — Пуазёйля:  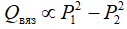         (2)

Выбирая производительность вакуумного насоса достаточно высокой, можно считать, что .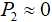

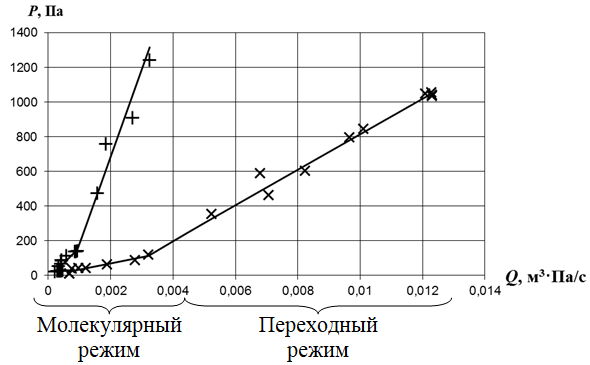
Таким образом, построив график (см. рис. 2) зависимости давления 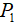 от расхода воздуха Q через пористый слой, можно выявить переходную зону по изменению характера зависимости с линейного на квадратичный.

Рис. 2 — График зависимости давления перед пористым материалом от расхода воздуха (при разной толщине слоя пористого материала):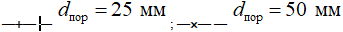 

На рис. 2 приведены результаты исследования для разных толщин пористого слоя. На графике видно, что начало переходной зоны характеризуется давлением 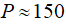 Па, которое соответствует длине свободного пробега молекул  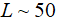мкм, а соответственно и 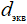. Такой же порядок величины можно получить методом микрофотографирования. Полученный размер пор соизмерим с диаметров волокна стекаловаты, что также, исходя из модельного представлением о изотропных волокнистых материалах [3], дает  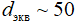мкм.

Важно отметить, что при работе на данной установке необязательно определять начало области вязкостного течения, так как попадание значения давления в переходную область будет характеризоваться возрастанием разброса показаний давления , вызванного нестабильностью диффузионных потоков ПГ.

В ходе исследования установлено, что начало переходной области мало зависит от толщины слоя пористого материала. Это объясняется тем, что в режиме кнудсеновской диффузии молекулы практически не сталкиваются друг с другом, а только со стенками порового канала. В исследуемых пористых материалах эквивалентный диаметр пор мало варьируется по величине, поэтому увеличение толщины слоя мало сказывается на вероятности прохождения молекулы через весь поровой канал, пока его длина несоизмеримо мала по сравнению с длиной свободного пробега молекулы. С другой стороны, толщина слоя пористой среды оказывает существенное влияние на величину давления, характеризующего окончание переходной зоны. Это объясняется тем, что с ростом давления в пористом материале за счёт увеличивающегося числа столкновений молекул ПГ не только со стенками порового канала, но и друг с другом. Чем длиннее поровой канал, тем более вероятными становятся столкновения молекул друг с другом, а, следовательно, вакуумное сопротивление увеличивается приблизительно пропорционально толщине слоя исследуемого материала.

Описанный выше способ может применяться только для оценки порядка эквивалентного диаметра пор, что связано с низкой точностью вакуумных измерений. Однако, для многих практических задач (например, в исследованиях химической кинетике реакций на пористых катализаторах, механических и теплофизических свойств строительных материалов и т. п.) достаточно определять только порядок величины диаметра пор.

Достоинством предложенного способа является возможность применять его для пористых, волокнистых и др. типов дисперсных сред, которые могут изменять свои порометрические свойства под действием избыточного давления или обладать гигроскопичностью.