МОДЕЛИРОВАНИЕ ФРАКТАЛЬНЫХ БРОУНОВСКИХ ИЗОБРАЖЕНИЙ
Полищук С.В.1, Петров К.А.2, Смехун Я.А.3
1Магистрант, 2магистрант, 3магистрант, Дальневосточный федеральный университет
МОДЕЛИРОВАНИЕ ФРАКТАЛЬНЫХ БРОУНОВСКИХ ИЗОБРАЖЕНИЙ
Аннотация
Предложен и исследован алгоритм моделирования фрактальных броуновских изображений. Установлено, что интегральная характеристика спектра броуновского изображения с параметром Херста a хорошо аппроксимируется степенной функцией с показателем 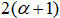 при
при 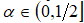 и показателем степени равным 3 для
и показателем степени равным 3 для 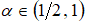 .
.
Ключевые слова: фрактальный броуновский процесс, пространственно-частотная фильтрация, структурная функция.
Polischuk S.V.1, Petrov K.A.2, Smekhun Y.A.3
1Undergraduate; 2undergraduate; 3undergraduate, Far Eastern Federal University
THE SIMULATION OF FRACTIONAL BROWNIAN IMAGES
Abstract
The modeling algorithm of fractal Brownian images has been proposed and studied. It is established that an integral characteristic of the spectrum of Brownian image with Hurst’s parameter is well approximated by a function power with an exponent 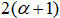 in
in 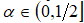 and the exponent which is equal to 3, for
and the exponent which is equal to 3, for 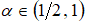 .
.
Keywords: the fractal Brownian process, spatial frequency filtering, a structure function.
Введение. Фрактальный анализ изображений проводится в тех случаях, когда необходимо установить, в какой степени, отображенные на изображениях объекты и структуры, проявляют фрактальные свойства.
Одним из наиболее распространенных критериев наличия фрактальных признаков у структур основан на использовании структурной функции первого порядка (математическое ожидание модуля приращения) и структурной функции второго порядка (математическое ожидание квадрата модуля приращения).
Моделирование фрактальных броуновских изображений. Случайный процесс 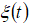 с математическим ожиданием
с математическим ожиданием 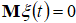 , удовлетворяющий условию:
, удовлетворяющий условию:
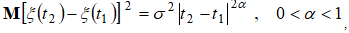 (1)
(1)
где a - показатель Херста, 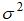 - приращение дисперсии за единицу времени, будем считать фрактальным броуновским. Других ограничений на процесс не накладывается. Можно показать, что для такого процесса спектральная плотность существует и совпадает с известной степенной зависимостью только для значений показателя
- приращение дисперсии за единицу времени, будем считать фрактальным броуновским. Других ограничений на процесс не накладывается. Можно показать, что для такого процесса спектральная плотность существует и совпадает с известной степенной зависимостью только для значений показателя 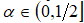 . В интервале
. В интервале 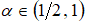 спектральная плотность не существует, а периодограммная оценка показателя имеет постоянное значение, равное
спектральная плотность не существует, а периодограммная оценка показателя имеет постоянное значение, равное 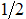 [1]. Этот факт наряду с нестационарностью фрактального броуновского процесса существенно ограничивает применение методов для моделирования фрактальных броуновских полей.
[1]. Этот факт наряду с нестационарностью фрактального броуновского процесса существенно ограничивает применение методов для моделирования фрактальных броуновских полей.
Для примера рассмотрим частный случай процесса (1) при условии, что 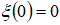 - процесс начинается в нуле, и его приращения – величины независимые. Тогда в соответствии с центральной предельной теоремой случайный процесс – нормальный с нулевым математическим ожиданием, дисперсией
- процесс начинается в нуле, и его приращения – величины независимые. Тогда в соответствии с центральной предельной теоремой случайный процесс – нормальный с нулевым математическим ожиданием, дисперсией 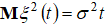 и параметром
и параметром 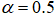 . Если
. Если 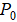 - вероятность события
- вероятность события 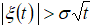 , то несложно получить
, то несложно получить 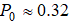 . Это означает, что примерно 1/3 всех траекторий процесса выходит за интервал
. Это означает, что примерно 1/3 всех траекторий процесса выходит за интервал 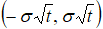 , что не может обеспечить стационарная модель.
, что не может обеспечить стационарная модель.
Используем тот факт, что в одномерном случае приращение 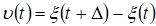 процесса
процесса 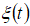 по интервалу фиксированной длительности Δ является стационарным в широком смысле случайным процессом с коэффициентом корреляции [13]
по интервалу фиксированной длительности Δ является стационарным в широком смысле случайным процессом с коэффициентом корреляции [13]
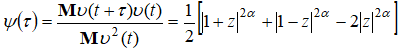 (2)
(2)
где 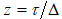 . Спектральная плотность
. Спектральная плотность 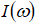 (ω-частота) процесса приращений
(ω-частота) процесса приращений 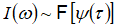 , где F - оператор преобразования Фурье. Процесс
, где F - оператор преобразования Фурье. Процесс 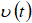 можно смоделировать, пропуская реализации «белого шума» через фильтр с передаточной функцией
можно смоделировать, пропуская реализации «белого шума» через фильтр с передаточной функцией 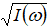 . Затем траектории процесса
. Затем траектории процесса 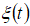 находятся интегрированием стационарных приращений
находятся интегрированием стационарных приращений 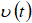 .
.
Двумерный процесс 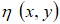 зададим в виде суперпозиции [2]
зададим в виде суперпозиции [2] 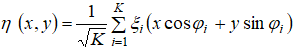 (3)
(3)
независимых фрактальных броуновских процессов 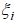
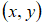 с параметром Херста a, математическим ожиданием
с параметром Херста a, математическим ожиданием 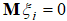 и структурной функцией вида (1),
и структурной функцией вида (1), 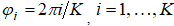 . В соотношении (3) каждое слагаемое представляет собой функцию двух аргументов (x,y). Эта функция – величина постоянная на прямой
. В соотношении (3) каждое слагаемое представляет собой функцию двух аргументов (x,y). Эта функция – величина постоянная на прямой 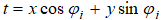 для любого фиксированного t и совпадает с фрактальным броуновским процессом в направлении, перпендикулярном этой прямой. Структурная функция поля η
для любого фиксированного t и совпадает с фрактальным броуновским процессом в направлении, перпендикулярном этой прямой. Структурная функция поля η
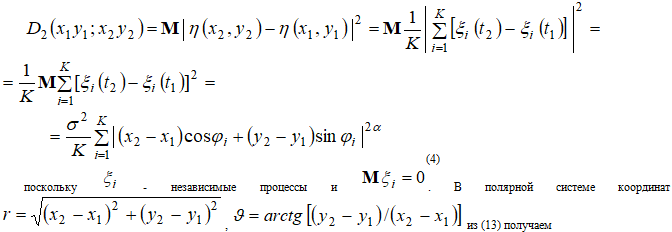
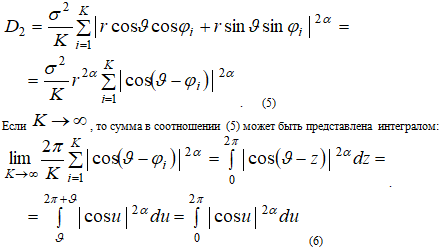 Таким образом, при большом K структурная функция
Таким образом, при большом K структурная функция 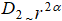 и, следовательно,
и, следовательно, 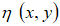 - фрактальное броуновское поле с параметром Херста a.
- фрактальное броуновское поле с параметром Херста a.
Для моделирования фрактальных броуновских изображений использовался следующий алгоритм. Генерировались из «белого шума» одномерные броуновские процессы 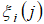 , с показателем Херста
, с показателем Херста 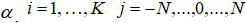 . Далее формировались K изображений, в которых строки заполнялась соответствующими значениями процесса
. Далее формировались K изображений, в которых строки заполнялась соответствующими значениями процесса 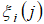 . Каждое изображение поворачивалось вокруг точки (0,0) на заданный угол
. Каждое изображение поворачивалось вокруг точки (0,0) на заданный угол 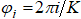 , и все K изображений суммировались. Затем из суммарного изображения вырезалась область размером
, и все K изображений суммировались. Затем из суммарного изображения вырезалась область размером 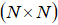 отсчетов с центром в точке (0,0). Статистический анализ смоделированных таким образом фрактальных броуновских изображений
отсчетов с центром в точке (0,0). Статистический анализ смоделированных таким образом фрактальных броуновских изображений 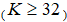 показал, что если
показал, что если 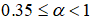 , то для функции
, то для функции 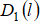 область скейлинга
область скейлинга 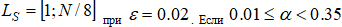 то при малых значениях l отклонения функции
то при малых значениях l отклонения функции 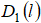 от степенной зависимости становятся значительными. Для устранения этих отклонений можно применить пространственно-частотную фильтрацию к уже смоделированным изображениям. Важно отметить, что интегральная характеристика оценки спектральной плотности
от степенной зависимости становятся значительными. Для устранения этих отклонений можно применить пространственно-частотную фильтрацию к уже смоделированным изображениям. Важно отметить, что интегральная характеристика оценки спектральной плотности 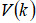 смоделированных фрактальных броуновских изображений для частот
смоделированных фрактальных броуновских изображений для частот 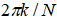 в интервале
в интервале 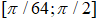 хорошо аппроксимируется степенной функцией
хорошо аппроксимируется степенной функцией 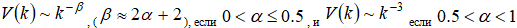 .
.
Заключение. В данной работе предложен и исследован алгоритм моделирования фрактальных броуновских изображений на основе генерирования одномерных реализаций фрактального броуновского процесса. Установлено, что существует достаточно широкий диапазон пространственных частот, в котором интегральная характеристика спектра броуновского изображения хорошо аппроксимируется степенной функцией 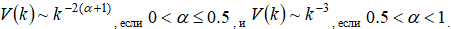
Список литературы
Кулешов Е.Л., Грудин Б. Н.Спектральная плотность фрактального броуновского процесса // Автометрия. 2013. Том 49, № 3. С.18 -24.
Yin Z.-M. New method for simulation of fractional Brownian motion // Journal of computational physics, 1996, № 127, P. 66-72.
