МЕТОДЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ, ПРИМЕНЯЕМЫЕ В СТРОИТЕЛЬНОЙ ЭКСПЕРТИЗЕ МАТЕРИАЛОВ

Бунтова О.С.¹, Бунтова Е.В.², Юсупова О.В.³

¹Студент, Самарский государственный архитектурно-строительный университет; ²кандидат педагогических наук, доцент, Самарская государственная сельскохозяйственная академия; ³Кандидат педагогических наук, профессор, Самарский государственный архитектурно-строительный университет

МЕТОДЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ, ПРИМЕНЯЕМЫЕ В СТРОИТЕЛЬНОЙ ЭКСПЕРТИЗЕ МАТЕРИАЛОВ

Аннотация

В статье рассмотрено практическое применение вероятностно-статистических методов к проведению строительной экспертизы.

Ключевые слова: статистическая, градуировочная, погрешность, репрезентативность, прочность, бетон.

 

Buntova O.S.¹, Buntova E.V.², Yusupova О.В.³

¹Student, Samara state University of architecture and construction; ²Candidate of pedagogical Sciences, associate Professor, Samara state agricultural Academy; ³Candidate of pedagogical Sciences, Professor, Samara state University of architecture and construction

METHODS OF MATHEMATICAL STATISTICS, APPLIED IN CONSTRUCTION MATERIALS EXAMINATION

Abstract

The article focuses on the practical application of probabilistic-statistical methods for construction expertise.

Keywords: statistics, calibration, accuracy and representativeness, strength, concrete.

Результаты исследования статистических данных методами математической статистики используют для принятия решения, т.е. для научных и практических выводов.

Исследование качественных и количественных характеристик отдельных строительных конструкций, их узлов, а также строительных объектов в целях установления их соответствия требованиям специальных правил, определение причин, условий и обстоятельств, механизма частичной или полной утраты объектами своих эксплуатационных свойств невозможно без проведения строительной экспертизы. В свою очередь проведение строительной экспертизы невозможно осуществить без проведения лабораторных исследований.

В лабораторных условиях проводят исследование образцов. Образцы, пробы при проведении строительной экспертизы позволяют установить физико – химические свойства строительных материалов и изделий.

 Данные лабораторных исследований можно рассматривать как статистические данные, обработка которых позволяет сделать практические выводы.

Таким образом, актуальность темы исследования очевидна.

Проблема исследования заключалась в выборе оптимальных методов математической статистики для выявления градуировочной зависимости между прочностью бетонных образцов и косвенной характеристикой прочности определенной двухпараметрическим методом, для контроля прочности монолитного бетонного покрытия автомобильной дороги.

В соответствии с проблемой исследования были поставлены задачи:

- обработать результаты испытаний на прочностью бетонных образцов; 

- установить градуировочную зависимость между прочностью бетонных образцов и косвенной характеристикой, в виде уравнения;

- построить график градуировочной зависимости;

- проверить условия градуировочной зависимости и сформулировать практический вывод по результатам проведенного исследования.

Проведенный анализ научной литературы позволил выделить три вида научной и прикладной деятельности в области статистических методов анализа данных [6]:

1) разработка и исследование методов общего назначения, без учета специфики области применения;

2) разработка и исследование статистических моделей реальных явлений и процессов в соответствии с потребностями той или иной области деятельности;

3) применение статистических методов и моделей для статистического анализа конкретных данных.

Внутри прикладной статистики выделяют задачи описания, оценивания и проверки гипотез [6].

Описание вида данных и механизма их порождения – начало любого статистического исследования. Для описания данных применяют как детерминированные, так и вероятностные методы. С помощью детерминированных методов анализируют те данные, которые имеются в распоряжении исследователя.

На первом этапе данные исследования (эксперимента) представляют в удобном для восприятия виде с помощью таблиц и диаграмм. Затем статистические данные анализируют на основе вероятностно-статистических моделей. Статистический анализ данных включает в себя целый ряд процедур и алгоритмов, выполняемых последовательно, параллельно или по более сложной схеме. На основе проведенного теоретического анализа научной  литературы, выделены основные этапы статистического анализа данных, полученных в результате лабораторного исследования [1].

Экономическая невыгодность проведения сплошного обследования и невозможность сплошного обследования указало на целесообразность изучения и проведения выборочного исследования.

Для получения хороших оценок характеристик генеральной совокупности необходимо, чтобы выборка была репрезентативной, т.е. достаточно полно представляла изучаемые признаки генеральной совокупности. 

В зависимости от конкретных условий для обеспечения репрезентативности применяют различные способы отбора: простой, при котором из генеральной совокупности извлекают по одному объекту; типический, при котором генеральную совокупность делят на «типические» части и отбор осуществляется из каждой части; механический, при котором отбор производится через определенный интервал; серийный отбор, при котором объекты из генеральной совокупности отбираются сериями и исследуют при помощи сплошного обследования. На практике пользуются сочетанием вышеупомянутых способов отбора.

Методами статистической обработки результатов лабораторных исследований [6] называют математические приемы, формулы, способы количественных расчетов, с помощью которых показатели, получаемые в ходе лабораторного исследования, можно обобщать, приводить в систему, выявляя скрытые в них закономерности. 

Некоторые из методов математико-статистического анализа позволяют вычислять элементарные математические статистики, характеризующие выборочное распределение данных, например выборочное среднее, выборочная дисперсия, мода, медиана и ряд других. Иные методы математической статистики, например дисперсионный анализ, регрессионный анализ, позволяют судить о динамике изменения отдельных статистик выборки. С помощью третьей группы методов, корреляционного анализа, факторного анализа, методов сравнения выборочных данных, можно достоверно судить о статистических связях, существующих между переменными величинами, которые рассматривают в лабораторном исследовании.

 Достоинства эксперимента по сравнению с наблюдением [6]:

1) возможность изучения явления в чистом виде, без влияния побочных факторов, затемняющих основной процесс;

2) в экспериментальных условиях можно получить результат более быстро и точно;

3) в эксперименте можно проводить испытания столько раз, сколько это необходимо.

Результат эксперимента или измерения всегда содержит некоторую погрешность. Целью математической обработки результатов эксперимента является не нахождение истинного характера зависимости между переменными или абсолютной величины какой-либо постоянной, а представление результатов наблюдений в виде простой формулы с оценкой возможной погрешности ее использования.

Выделены три основных типа ошибок измерений при проведении лабораторного исследования [2].

К первому типу отнесены систематические погрешности, которые обуславливаются постоянно действующими факторами и поэтому могут быть учтены при обработке результатов измерений.

Ко второму типу отнесены случайные ошибки, которые содержат в своей основе причины, не проявляющие себя отчетливо. Эти ошибки невозможно учесть как систематические ошибки. Анализ случайных ошибок является одним из разделов математической обработки экспериментальных данных. Случайные ошибки бывают как положительные, так и отрицательные, разной величины, не превосходящей определенного предела. Исключить случайные ошибки при измерении нельзя, однако применение метода теории ошибок позволяет более точно установить возможную ошибку окончательного результата измерений.

К третьему типу отнесены абсолютная и относительная ошибки. Абсолютная ошибка – разница в абсолютных цифрах между наиболее достоверным значением определяемой величины и полученным результатом, выраженная в единицах измеряемой величины. Относительная ошибка – отношение абсолютной ошибки к  среднему значению измеряемой величины, выраженное в процентах. Относительная ошибка дает более наглядное представление о точности измерений.

 Проведенный теоретический анализ позволил выявить основу статистической обработки результатов измерений – оценку точности измерений при малом и большом числе измерений.

В выбранной методике лабораторного исследования прочность бетона определяли по  установленным градуировочным зависимостям между прочностью бетонных образцов по ГОСТ 10180-90 и косвенным характеристикам прочности [5]. Косвенными характеристиками прочности являются:

- значение отскока бойка от поверхности бетона;

- параметр ударного импульса (энергия удара);

- соотношение диаметров отпечатков на бетоне и стандартном образце при ударе индентора или вдавливании его в поверхность бетона;

- значение напряжения, необходимого для местного разрушения бетона при отрыве приклеенного к нему металлического диска, равного усилию отрыва, деленному на площадь проекции поверхности отрыва бетона на плоскость диска;

- значение усилия необходимого для скалывания участка бетона на ребре конструкции;

- значение усилия местного разрушения бетона при вырыве из него анкерного устройства.

Механические методы неразрушающего контроля применяют для определения прочности бетона всех видов нормированной прочности, контролируемых по ГОСТ 10180-90 [5], а также для определения прочности бетона при обследовании и отбраковки конструкций.

Для методов упругого отскока, ударного импульса, пластической деформации и отрыва градуировочные зависимости устанавливают конкретно для каждого вида прочности; для методов отрыва со скалыванием и скола ребра допускается устанавливать единую градуировочную зависимость независимо от вида прочности.

Градуировочную зависимость устанавливают при изменении вида крупного заполнителя, технологии производства бетона, при введении добавок, а для методов отскока, ударного импульса и пластической деформации – также при изменении вида цемента, внесении количественных изменений в номинальный состав бетона, превышающих по расходу цемента ±20%.

За единичное значение косвенного показателя прочности при установлении градуировочной зависимости принимали среднее арифметическое значение этой величины в серии образцов, используемых для определения единичного значения прочности.

Градуировочная зависимость должна иметь среднее квадратическое (остаточное) отклонение S_т, не превышающее 12% при использовании серии образцов, и 15% при использовании отдельных образцов от среднего значения прочности .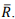

Прочность бетона в контролируемом участке конструкции определяли по градуировочной зависимости, при условии, что измеренные значения косвенного показателя находятся в пределах между наименьшим и наибольшим значениями косвенного показателя в образцах, испытанных при построении градуировочной зависимости.

При использовании анкерных устройств, прочность бетона R, МПа можно вычислять по градуировочной зависимости по формуле

R=m₁∙m₂∙P,

где m₁ - коэффициент, учитывающий максимальный размер крупного заполнителя в зоне вырыва и принимаемый равным 1 при крупности 50 мм и 1,1 при крупности более 50 мм; m₂ - коэффициент пропорциональности для перехода от усилия вырыва, кН, к прочности бетона, МПа; P - усилие вырыва анкерного устройства, кН.

Уравнение зависимости «косвенная характеристика – прочность» принимают линейным по формуле

R_H=a₀+a₁H,

где  R_H - прочность бетона, МПа; H - косвенная характеристика.

Коэффициенты a₀ и a₁ рассчитывают по формулам:

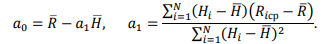
Среднее значение прочности R, определенные путем испытания образцов по ГОСТ 10180-90 [3], и косвенных характеристик 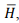 необходимых для определения этих коэффициентов, рассчитывают по формулам

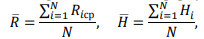
где  R_iср и H_i - соответственно значения прочности и косвенной характеристики для отдельных серий по ГОСТ 10180-90 [5]; N- число серий (или отдельных образцов), использовавшихся для построения градуировочной зависимости.

После построения градуировочной зависимости по формуле R_H=a₀+a₁H проводили ее корректировку путем отбраковки единичных результатов испытаний, не удовлетворяющих условию

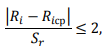
где  S_r- остаточное среднее квадратическое отклонение, определенное по формуле:

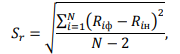
где R_iн - прочность бетона в i-й серии образцов, определенная по градуировочной зависимости по формуле R_iн=a0-a_iH_i.

Погрешность определения прочности бетона по установленной зависимости оценивали по формуле:

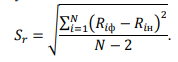
Если

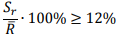
то проведение контроля и оценка прочности по полученной зависимости не допускаются.

В соответствии с установочной градуировочной зависимостью по полученным косвенным характеристикам определяли прочность бетона. Вычисляли среднее значение косвенных характеристик по формуле:

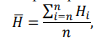
где  n - число серий, испытанных для проверки градуировочной зависимости.

Затем разделяли испытанные серии образцов, единичные значения косвенной характеристики которых  не превышают их среднее значение :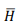

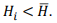
Ко второй группе отнесли все остальные серии, т.е. те, у которых

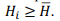
Градуировочная зависимость допускается к дальнейшему применению при одновременном выполнении следующих условий [5]:

1) разность R_iф-R_iн не имеет одинакового знака в пяти из шести испытанных серий образцов;

2) среднее квадратическое отклонение (S_n) прочности бетона в испытанных сериях, определенное по формуле

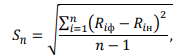
не должно превышать более чем в полтора раза среднее квадратическое отклонение используемой градуировочной зависимости

S_n<1,5S_r;

3) значение разности R_iф-Ri_н  не должно иметь одинакового знака для серий образцов первой и второй групп.

При невыполнении хотя бы одного из условий градуировочную зависимость устанавливают заново.

 Результатом проведенных лабораторных исследований явилась обработка результатов испытаний и выявления градуировочной зависимости между прочностью образцов бетона и косвенной характеристикой прочности.

В итоге был получен  результат градуировочной зависимости для определения прочности бетона монолитных конструкций класса В30

R_H=9,09+1,08H.

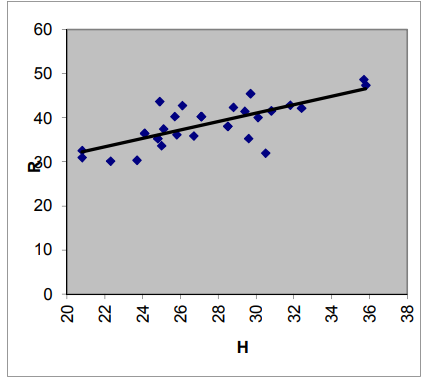
Рис. 3 График градуировочной зависимости для определения прочности бетона монолитных конструкций класса В35 ударно-импульсным измерителем прочности «ОНИКС 2.51»

Построенный график градуировочной зависимости дает возможность наблюдать, что облако единичных результатов испытаний расположено вдоль построенного графика градуировочной зависимости, а это указывает на правильность найденной градуировочной зависимости.

Среднее квадратическое отклонение прочности бетона

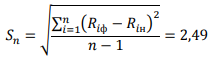
не превышает более, чем в 1,5 раза среднее квадратическое отклонение используемой градуировочной зависимости

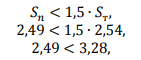
что указывает на выполнение условия проверки градуировочной зависимости.

Таким образом, из множества вероятностно-статистических методов выявлены методы, применимые к строительной экспертизе материалов.