ЧИСЛЕННОЕ РЕШЕНИЕ СТОХАСТИЧЕСКОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ МЕТОДОМ ЭЙЛЕРА-МАРУЯМЫ

Кузнецова И.Ю.

Аспирант, Южный федеральный университет

ЧИСЛЕННОЕ РЕШЕНИЕ СТОХАСТИЧЕСКОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ МЕТОДОМ ЭЙЛЕРА-МАРУЯМЫ

Анностация

В данной статье описан один из наиболее популярных численных методов решения стохастических дифференциальных уравнений. В статье даны определение основной концепции, описание простейшего численного метода, а также понятие сходимости решений стохастических дифференциальных уравнений. Решениями являются непрерывные вероятностные процессы, что может быть использовано при прогнозировании процесса потребления энергоресурсов.

Ключевые слова: стохастические дифференциальные уравнения, численные методы, сходимость, порядок аппроксимации.

Kuznetsova I.Y.

Postgraduate student, Southern Federal University.

NUMERICAL SOLUTION OF STOCHASTIC DIFFERENTIAL EQUATION BY EULER-MARUYAMA METHOD

Abstract

In the article described one of the most popular numerical methods for solving stochastic differential equations. It includes a review of fundamental concepts, a description of elementary numerical methods and the concepts of convergence and order for stochastic differential equation solvers. The solutions will be continuous stochastic processes that can be used for prediction process of energy consumption.

Keywords: stochastic differential equations; numerical methods; convergence; order for solvers.

СДУ стали стандартными моделями финансовых величин, таких как цены активов, процентная ставка, и их деривативов. В отличие от детерминированных моделей, таких как обыкновенные дифференциальные уравнения, которые имеют единственное решение для каждого соответствующего начального условия, СДУ имеют решения, являющиеся стохастическими процессами с непрерывным временем. Методы численного решения СДУ основаны схожей технике решения обыкновенных дифференциальных уравнений, но обобщены для обеспечения стохастической динамики.

Простейшим эффективным численным методом аппроксимации обыкновенных дифференциальных уравнений является метод Эйлера. Метод Эйлера-Маруяма является аналогом метода Эйлера для обыкновенных дифференциальных уравнений.

Рассмотрим стохастическое дифференциальное уравнение, описывающее динамику потребления электроэнергии в ВУЗе [2,3]:

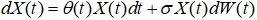          (1)

с начальным условием

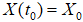            (2)

где 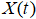 — потребление энергоресурсов (электроэнергии),  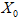— данные по потреблению в начальный момент времени  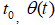— функция, учитывающая сезонные изменения, σ — коэффициент, учитывающий изменения, носящие случайных характер,  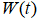— винеровский процесс.

Зафиксируем равномерную сетку

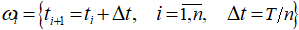
где T — длина рассматриваемого временного промежутка, n — количество месяцев в рассматриваемом промежутке времени, Δt — шаг по времени.

Также введем следующие обозначения:

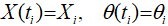
Проинтегрируем исходное уравнение (1) на промежутке 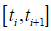. Получим

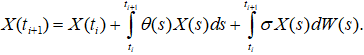            (3)

Переходя к конечным разностям из (3) и определения стохастического интеграла, имеем,

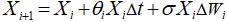       (4)

где 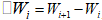 — приращение винеровского процесса, которое, исходя из свойств винеровского процесса, можно записать в виде:

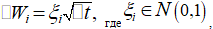            (5)

то есть ξ_i — случайная величина, распределенная по нормальному закону с нулевым математическим ожиданием и единичной дисперсией.

Найдем порядок сходимости метода Эйлера-Маруямы для (1).

Говорят, что численное решение 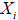 с шагом по времени  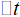сильно сходится к точному решению  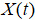в момент времени T, если

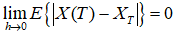
В дальнейшем мы будем определять скорость сильной сходимости приближенного решения через понятие порядка. Решение СДУ сходится сильно с порядком m, если математическое ожидание ошибки имеет m-ый порядок от шага, то есть для любого момента времени T,

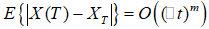
для достаточно малого размера шага 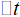. Это определение обобщает стандартные критерии сходимости для обыкновенных дифференциальных уравнений, и сводится к обычному определению, когда стохастическая часть уравнения обращается в нуль.

Воспользуемся разложением Тейлора-Ито на 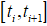, которое для поставленной задачи запишется в виде:

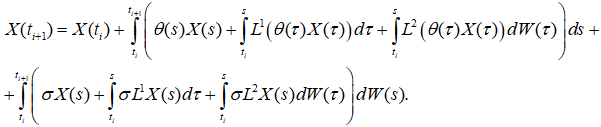            (6) Вычислив повторные интегралы, разложение (6) можно записать в виде:  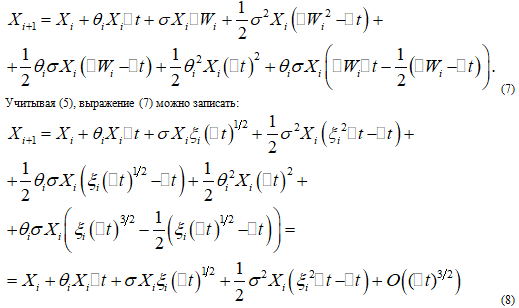 Откуда получим, что  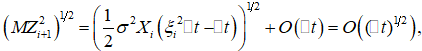            (9)

где 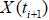 — точное решение СДУ (1), а  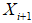 — численное решение СДУ (1) по методу Эйлера-Маруямы (4) в точке .

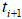Хотя метод Эйлера для обыкновенных дифференциальных уравнений имеет первый порядок, метод Эйлера-Маруямы для стохастических дифференциальных уравнений имеет порядок 0,5. Этот факт доказан Гикхманом и Скороходовым в 1972 году.

На основании данных по потреблению электроэнергии за 2010-2011гг. общежитиями студенческого городка ЮФУ в г. Таганроге и предложенной модели (1) были получены следующие прогнозные значения потребления электроэнергии на 2012 год, которые были сравнены с данными по потреблению электроэнергии за тот же период.

При применении метода Эйлера-Маруямы (4) к модельному уравнению (1) были получены следующие результаты:

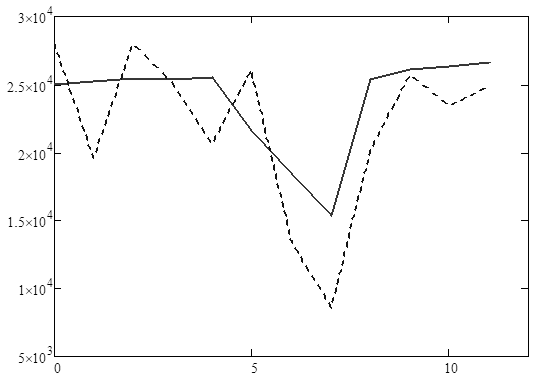
Рис. 1 - График потребления электроэнергии на 2012 г.

——— — прогнозные данные на 2012 г. по потреблению электроэнергии,

полученные с помощью метода Эйлера-Маруямы (2.27);

- - - - - - — реальные данные по потреблению электроэнергии за 2012 г.

  Определение качества модели проводилось по следующим параметрам:

1. Модельная погрешность:

           (10)

где 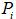  — фактическое значение потребления электроэнергии в i-ый момент времени,  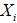— значение потребления электроэнергии, полученное с помощью модели (1), в i-ый момент времени.

2. Среднеквадратичное отклонение:

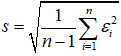
где 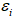 — модельная погрешность в i-ый момент времени, определяемая формулой (10), n — длительность периода прогнозирования в месяцах.

3. Средний процент ошибки:

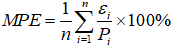
где 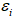 — модельная погрешность в i-ый момент времени, определяемая формулой (10),  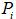— фактическое значение потребления электроэнергии в i-ый момент времени,  n— длительность периода прогнозирования в месяцах.

4. Средняя относительная ошибка прогноза:

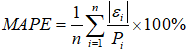
где 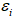 — модельная погрешность в i-ый момент времени, определяемая формулой (10),  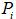— фактическое значение потребления электроэнергии в i-ый момент времени,  n— длительность периода прогнозирования в месяцах.

5. Коэффициент детерминации:

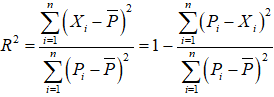
где 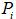— фактическое значение потребления электроэнергии в i-ый момент времени,  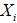— значение потребления электроэнергии, полученное с помощью модели (2.24), в i-ый момент времени,

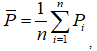
где n  — длительность периода прогнозирования в месяцах.

6. Индекс Тейла:

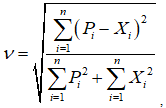
где 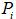 — фактическое значение потребления электроэнергии в ш-ый момент времени,  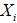— значение потребления электроэнергии, полученное с помощью модели (1), в i-ый момент времени,

Полученные результаты представленным в таблице 1.

Таблица 1

	Метод Эйлера-Маруямы
Среднеквадратичное отклонение (нормированное)	0,167
Средний процент ошибки	10,2%
Средняя относительная ошибка прогноза	18,3%
Коэффициент детерминации	0,61
Индекс Тейла	0,123

На основании полученных результатов можно сделать вывод о применимости рассматриваемой модели (1) к прогнозированию потребления электроэнергии.

Численные методы решения стохастических дифференциальных уравнений играют важную роль при анализе случайных процессов. Несмотря на то, что скорость сходимости к сильному решению для метода Эйлера-Маруямы составляет всего 0,5, его популярность в сфере финансов обусловлена тем, что он «прост» в построении разностной схемы и не требует большого объема вычислительных ресурсов. Это позволяет применять его для определения качества построенных моделей. Применение численных методов более высоких порядков ведет к резкому возрастанию необходимых вычислительных ресурсов, при этом точность прогноза может изменяться незначительно.