НЕСИММЕТРИЧНЫЕ ПРИНУДИТЕЛЬНЫЕ ТАНЦЫ ЦИЛИНДРИЧЕСКОЙ КРЫШКИ, АРМИРОВАННОЙ СТЕРЖНЯМИ

Известно, что одной из наиболее актуальных проблем механики деформируемого твердого тела являются аналитические выражения для расчета искомых в исследуемых вопросах величин. В данной работе одна из характеристик динамической жесткости цилиндрического пласта, на который действует сжимающая сила в направлении оси, армирована стержнями и контактирует с жидкостью — удельные частоты горных пород и это получение аналитических выражений для расчета частот, исследование вынужденных движений, вызванных воздействием внешней силы, гармонически изменяющейся во времени, еще раз подтверждает актуальность темы получения аналитических выражений для расчета смещений точек цилиндрического тела.

Когда мы говорим о цилиндрической юрте, армированной стержнями, имеется в виду сочетание цилиндрической юрты с противоположно деформированными цилиндрическими стержнями. Таким образом, используются два метода исследования состояния смещения-деформирования такой конструкции под действием статических и динамических сил. Первый метод заключается в моделировании конструкции как конструктивно-ортотропной страны. Сущность второго метода состоит в том, что система уравнений, характеризующих процесс деформирования конструкции, рассчитывается с учетом дискретного расположения стержней. В частном случае из этой системы можно получить систему уравнений, характеризующую процесс деформирования конструктивно-ортотропного цилиндрического тела путем перехода к пределу, когда число колец увеличивается бесконечно.

Изучаемая нами система состоит из цилиндрической оболочки, укрепленной стержнями и жидкости, полностью заполняющей ее внутреннюю часть. Поэтому для исследования динамики такой системы воспользуемся системой уравнений движения жидкости и добавленными к ним контактными условиями.

В.З. Власов

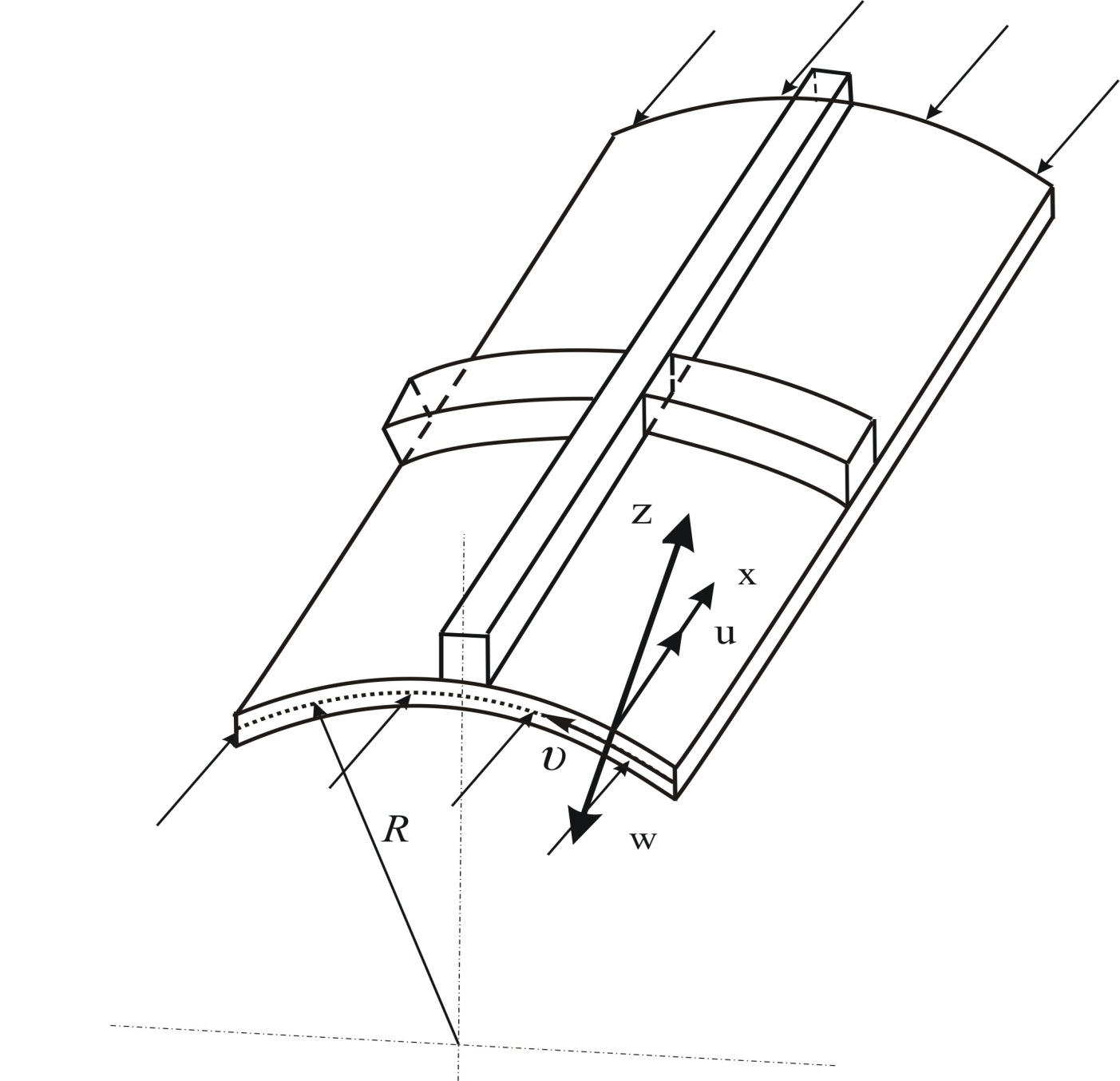
Рисунок 1 - Соприкасающаяся со средой цилиндрическая оболочка, подкрепленная стержнями, нагруженными к действию сжимающей силы

DOI:10.23670/IRJ.2023.137.9.1

Предполагается, что оси координат совпадают с основными линиями разъема ложа и вдоль этих линий стержни находятся в жестком контакте с ложем. Работа

[5]

была посвящена нахождению удельных частот вращения продольных и круговых стержневых армированных катушек. В

[6]

с помощью численных методов были найдены удельные частоты качания стержней, армированных стержнями. Система уравнений равновесия со стержнями на поверхности в произвольном положении была получена в работах

[7]

. Следует отметить, что характеристические и вынужденные движения гладких цилиндрических подшипников, контактирующих с окружающей средой, изучались в работах

[8]

,

[9]

,

[10]

. В работах

[11]

,

[12]

исследовались вынужденные трещины гладких цилиндрических подшипников, контактирующих с окружающей средой.

Предположим, что на цилиндрическое тело действует гармоническая сила

(1)

В выражении (1)  – амплитуда силы  – скорость изменения во времени, ,  – соответственно, являются волновое число в направлении оси круга и цилиндра.

Если он находится под действием градиента давления, его потенциальная энергия определяется следующим образом

(2)

Кинетическая энергия армированной балки равна:

(3)

Используя решающее условие удара Остроградского-Гамильтона, по выражениям (2) и (3) можно получить выражение поведения стержневого армированного грунта:

(4)

 – эффект Гамильтона,  является функцией Лагранжа. В уравнении (4) если провести работу вариатора и , , , считая вариации произвольными и независимыми, получаем следующую систему уравнений движения:

(5)

Получаем систему уравнений движения при перемещениях конструктивного ортотропного цилиндрического тела:

(6)

Здесь .

Распространение малых возбуждений в идеальной жидкости выражается следующим уравнением:

(7)

Здесь  – потенциал жидкости, – скорость диффузии вещества в жидкости. В гармоническом случае преобразуем уравнение (7) в уравнение Хельмольца:

(8)

Когда жидкость несжимаемая, поскольку , (8) преобразуется в уравнение Лапласа:

(9)

Если жидкость представляет собой идеальную жидкость с двухфазными пузырьками, то распространение малых скачков напряжения в такой жидкости определяется следующим уравнением

(10)

Здесь ;  – фактическая плотность нефти и газа;  – статическое давление;  – плотность смеси;  – объем пузырьков газа; значения параметров в равновесии соответствуют нулевому показателю; 

В систему уравнений движения (6), уравнений движения жидкости (7) и (10) добавляются контактные условия. Предполагается, что нормальные составляющие скорости и давления на поверхности контакта с жидкостью равны, а тангенциальные перемещения равны нулю:

(11)

Здесь  являются составляющими силы давления, оказываемой жидкостью на тело.

Найти потенциал, входящий в выражение (8), можно следующим образом:

(12)

Это выражение можно записать в виде (8) в цилиндрической системе координат:

(13)

Здесь 

Общее решение уравнения (13) с помощью двух функций Бесселя можно записать следующим образом:

(14)

 зависит от значений параметра . Параметр  напишем следующим образом:

 когда (13) попадает в следующий порядок:

Решения последнего уравнения функции Бесселя  и  Поскольку жидкость заполняет внутреннюю часть цилиндрического тела, она будет поступать в область решения задачи с направлением . В этот момент, поскольку функция неограничена, решение уравнения Бесселя выглядит следующим образом:

(15)

зная выражение потенциала, можно определить давление жидкости и радиальную скорость  ее узлов [3]:

(16)

Используя выражения (15) и (16), получаем:

(17)

Решение системы динамики движения (5) ищется следующим образом:

(18)

Здесь – константы, – число волн в круговом направлении,  – число полуволн вдоль центра цилиндра,  – круговая частота.

Если использовать первое из выражений (11), решения (17) и (18), то константу  можно выразить через :

Мы можем записать это выражение в (17):

Если записать в это уравнение , то получим для значения давления на контакте:

(19)

Системы уравнений движения грунта и жидкости, армированные стержнями (7)-(10), совместно с контактными условиями (11) позволяют решить задачу о свободных движениях конструктивно-ортотропной системы грунт-флюид. Другими словами, исследование свободных движений ортотропного цилиндрического основания, контактирующего с твердой средой и жидкостью, сводится к интегрированию системы уравнений конструктивно-ортотропного основания и уравнения движения жидкости в условиях контакта. Если принять в (6) системе уравнений величины с индексом «с» равными нулю, то получим систему уравнений движения для перемещений цилиндрических оболочек, на которую действует сжимающая сила вдоль оси и внутренняя область заполнена жидкостью, укреплена только продольными стержнями:

(20)

Используя систему уравнений движения (20) и их решения (18), выражение (19) давления цилиндра на землю жидкостью и выражение (20), получим систему неоднородных линейные уравнения относительно констант :

(21)

(21) представляет собой систему неоднородных линейных уравнений, обусловленную  константами системы. Мы можем легко определить константы  из этой системы:

Здесь .

 константы следующие:

Если записать выражения констант  в (18), то можно найти перемещения точек цилиндрической опоры, на которую действует осевая сила и внутренняя область которой заполнена жидкостью, армированной стержнями:

(22)

Когда жидкость не сжата:

(23)

При впитывании жидкости:

(24)

Если записать выражение константы входящей в (21), в (19), получим для значения давления на контакте:

(25)

По тому же правилу, если использовать логарифмическую производную функции Бесселя :

с учетом соотношений

можно упростить выражение (25).

Когда жидкость не сжата:

При впитывании жидкости:

Зависимость отношения  из  – входящего в выражения (22), рассчитывалась численным методом. Для других физических и геометрических параметров, характеризующих систему, были приняты следующие числовые значения:

Результаты расчетов приведены на рис. 2.

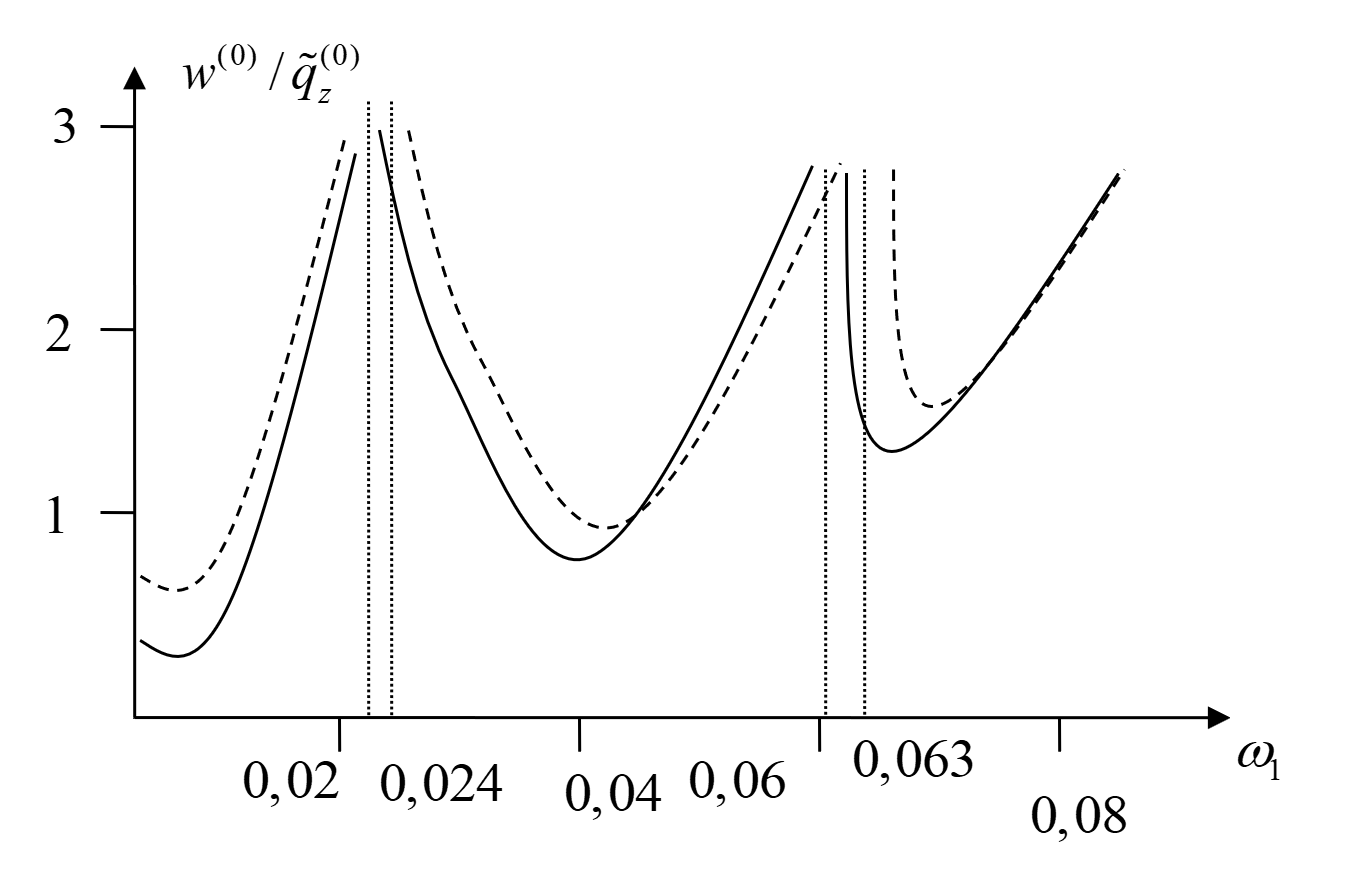
Рисунок 2 - Зависимость соотношения w(0) / qz(0) из ω1

Примечание: штриховые линии соответствуют несжимаемым случаям, а сплошные линии – сжимаемым случаям

DOI:10.23670/IRJ.2023.137.9.2

Как видно из графика, перемещение цилиндрического стержня не ограничено на резонансных частотах. Резонансные частоты соответствуют значениям , отмеченным на графике, а учет сжатия жидкости приводит к уменьшению этих частот по сравнению со случаем, когда жидкость не сжата. Для расчета перемещений на резонансных частотах и ​​вокруг них необходимо учитывать более реалистичное свойство жидкости, такое как ее вязкость. 

В статье впервые создана физико-математическая модель исследования свободных и вынужденных движений цилиндрического стержня, армированного стержнями и контактирующего с окружающей средой под действием осевой силы. Рассмотрены несимметричные случаи движений. Установлена ​​частотная кривая системы и найдены ее кривые асимптотическим методом. Изучено влияние геометрических, физических и механических параметров, характеризующих систему, на эти частоты. 

При решении данной задачи использовались уравнения теории состояний и уравнения гидродинамики. Полученное частотное уравнение системы исследовано асимптотическим методом. В процессе расчета использовалась логарифмическая сумма функции Бесселя. Трансцендентные уравнения, полученные с помощью логарифмического суммирования функции Бесселя, были объединены с алгебраическими уравнениями и найдены их корни.

Он основан на правильной постановке задачи, использовании точных решений гидродинамического уравнения, проверке точности полученных уравнений и схемы решения системы уравнений. Полученные формы сочетают в себе известные физические и математические закономерности.

Результаты, полученные в статье, могут быть использованы при исследовании характеристик динамической жесткости нефти и газопроводов, армированных стержнями, цилиндрических конструкций, контактирующих с жидкостью, применяемых в промышленности и гражданском строительстве, а также элементов конструкций.