ОБ ИССЛЕДОВАНИИ АРТИЛЛЕРИЙСКОЙ КОНТРБАТАРЕЙНОЙ БОРЬБЫ В ВИДЕ МАТРИЧНОЙ ИГРЫ
ОБ ИССЛЕДОВАНИИ АРТИЛЛЕРИЙСКОЙ КОНТРБАТАРЕЙНОЙ БОРЬБЫ В ВИДЕ МАТРИЧНОЙ ИГРЫ
Аннотация
При ведении современных боевых действий обеим сторонам целесообразно иметь объективные оценки степени успешности в достижении своих целей и оптимизировать их.
Такая ситуация ближе всех к математической модели матричных игр с нулевой суммой, когда в любом случае один участник должен проиграть не больше гарантированной величины, а другой – выиграть не больше той же величины. Эти условия служат основой проделанного исследования.
Найдены оптимальные стратегии для каждой из сторон, показывающие с какой вероятностью они должны неожиданным для противника образом предпринимать различные действия.
Предложенная модель достаточна адекватна рассматриваемой задаче и позволяет при определенных предположениях получить количественные рекомендации по оптимизации действий участников артиллерийской дуэли.
1. Введение
Очевидно, что во избежание длительных и дорогостоящих поисков решения многих серьезных задач «наощупь», «по здравому смыслу», «волевым образом» и т.д. необходим научный анализ. Это в первую очередь относится к военным и экономическим задачам, для решения которых еще до второй мировой войны, как указывали Морз Ф.М. и Кимбел Д.Е. стало зарождаться направление, называемое теперь исследованием операций. Уже тогда в вооруженных силах США и Англии были сформированы специальные научные группы для подготовки решений по способам организации и обеспечения боевых действий .
Упоминания примеров такого рода можно найти, в частности, в ставшей классической работе Вентцель Е.С. , когда одна сторона планирует оптимальную для нее организацию авианалета, а другая заботится об уменьшении возможного ущерба от налета. Рассматриваемые в этих задачах операции являются управляемыми с обеих сторон, причем согласовать их деятельность как совместную и свести, например, к поиску экстремума функции нескольких переменных невозможно.
Однако возможно найти некий «стихийный» компромисс, при котором выигрыш одной и проигрыш другой стороны ограничены одной величиной «цены игры» и при многократном повторении могут быть достигнуты статистически в виде некоторой наиболее вероятной «седловой точки» поверхности показателя эффективности. При этом рассчитываются обоюдно-оптимальные распределения выбираемых действий, а сами действия каждый раз должны осуществляться каждой из сторон неожиданно для другой.
Обязательным условием модели матричных игр, входящей в раздел теории операций является дискретность арсенала возможностей обеих сторон. В то же время встречаются весьма актуальные задачи, в которых это условие выполняется лишь для одной стороны. В качестве такого практического примера здесь предлагается артиллерийская дуэль, в которой лишь одна сторона может дискретно выбирать вид траектории для обстрела.
Общих способов построения математических моделей не существует. В каждом конкретном случае модель строится, исходя из целевой направленности операции и задачи исследования, с учетом требуемой точности решения, а также точности, с какой могут быть известны исходные данные (Афанасьев М.Ю., Багриновский К.А., Матюшок В.М. ).
К числу предшественников основополагающих исследований различных дуэлей Вентцель Е.С. , Неймана Дж. и Моргенштерна О. . Морз Ф.М. и Кимбела Д.Е. следует отнести прежде всего:
- дуэль двух танков в работе Зачриссона Л.Э., , где требование «нулевой суммы» выражается постоянством суммы вероятностей поражения каждого из участников и при определенных интуитивных предположениях получено, что оптимальное поведение включает кусочно-непрерывные функции;
- дуэль бомбардировщика с истребителем в работе Кэйвуда Т.Э. и Томааса С.Дж. , где проведен многоступенчатый анализ, включающий учет скорострельности и боекомплекта снарядов, а также привлечение большого объема сведений о тактике ведения огня, которые, как правило, неизвестны.
Саати Т.Л. , рассматривал военный конфликт между двумя странами, каждая из которых должна сделать простой выбор: продолжать или не продолжать эскалацию конфликта, как игровую ситуацию. Если одна сторона проводит эскалацию, а другая нет, то первая сторона одерживает победу. Если обе стороны проводят эскалацию, то они обе терпят убытки по сравнению с политикой деэскалации.
Общее моделирование процесса нанесения огневого удара любыми видами оружия представлено Чуевым Ю.В. . Этот процесс можно моделировать как с целью включить его в общую модель исследования, так и с целью отыскать оптимальные способы нанесения огневого удара и анализа влияния различных факторов на его успешность (в том числе таких, как время, надежность и т.д.).
2. Постановка задачи
В представленной работе возникла идея – во избежание излишних усложнений и неопределенности условий – изменить задачу таким образом, чтобы с позиций модели матричной игры найти обоюдно-оптимальное поведение для обоих участников дуэли простым и наглядным графо-аналитическим способом.
Такой подход представляется достаточно оправданным, а решение конкретной задачи артиллерийской дуэли даже с некоторой долей предположений является актуальным, а его наличие и оптимальность гарантируется основами теории матричных игр (Нейман Дж. и Моргенштерн О. ).
Отдельная особенность любой задачи – подобрать конкретный достаточно адекватный показатель эффективности, представляющий интерес для обеих сторон. Здесь – в отличие от других подобных исследований – в качестве такого показателя выбрана вероятность перехвата снаряда, обратно пропорциональная оценкам величины ошибок встречи двух снарядов в воздухе с учетом наибольшей безопасности обороняющейся стороны.
Участники актуальной задачи артиллерийской дуэли преследуют прямо противоположные цели: стреляющая батарея – поразить батарею противника, а обороняющаяся батарея – предотвратить это, перехватив снаряд в полете. При этом первая батарея может практически всегда (за исключением стрельбы под 45°) выбирать одну из двух траекторий: настильную или навесную. Зададимся вопросом наиболее рационального (эффективного) выбора траектории первой батареи, а также выбора места перехвата снаряда второй батареей. Постановка задачи близка к модели антагонистической матричной игры с нулевой суммой. Для применения этой модели выбор места перехвата снаряда сделан также дискретным путем задания трех условных стратегий: вблизи атакующей батареи, вблизи точки наивысшего подъема снаряда и вблизи обороняющейся батареи. Эта модель решения поставленной задачи с разработанным аппаратом представляет интерес благодаря своей наглядности и глубинному соответствию сути задачи.
Задача: Найти оптимальные стратегии противников в артиллерийской дуэли двух батарей методом антагонистических матричных игр с нулевой суммой.
Поставленная задача расчета обстоятельств артиллерийской дуэли преследует двойственную цель:
– с позиций объективного критерия матричной игры получить оптимальный выбор поведения обоих участников и
– методическую: исследовать и показать применение теории матричных игр для практики простыми средствами.
Как было сказано выше, математическая модель матричной игры с нулевой суммой нацелена на поиск компромисса в выборе среди множеств возможных ходов двух участников таких «оптимальных» частот (вероятностей (, …,
) и (
, …,
), где
и
– количество возможных ходов первого и второго участников соответственно) их применения, которые при многократном повторении игры позволят в среднем, независимо от действий противника, одному из них проиграть не больше, а другому выиграть не больше некоторой величины, называемой «ценой игры» E. Процедура реализации этой идеи в общем случае приводит к решению довольно громоздкой задачи линейного программирования. Однако, если, например, у одного из игроков имеется всего два хода, то задача легко решается графически.
3. Описание модели
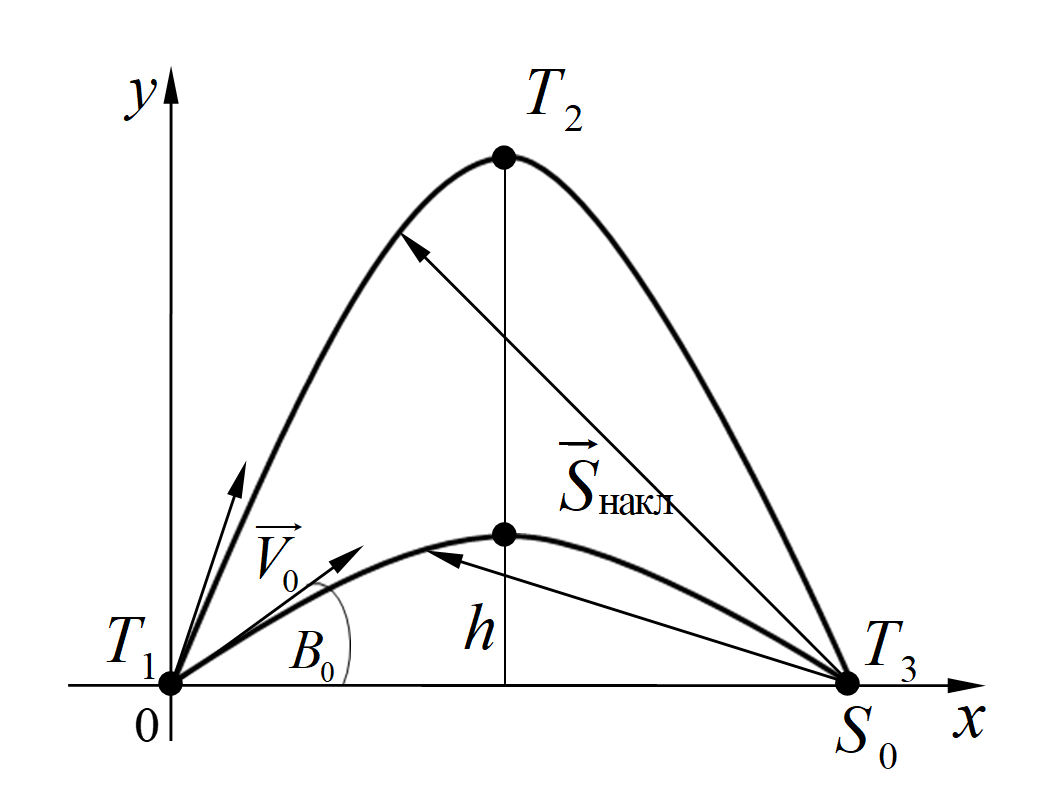
Рисунок 1 - Схема настильной и навесной траекторий полета снаряда
Полагая = 0,6 км/с, получаем
= 31,8 км.
Зададим степень вероятности перехвата (безопасного уничтожения) летящего снаряда в воздухе обороняющей объект батареей (весовую функцию) в виде:
где – расстояние от снаряда до батареи перехвата (по наклонной);
– проекция скорости снаряда на картинную плоскость для батареи перехвата (на ортогональное к лучу зрения
направление);
и
– задаваемые размерные коэффициенты.
Предложенное выражение учитывает, что:
а) вероятность поражения движущейся цели обратно пропорциональна квадрату суммарной ошибки , которая, в свою очередь, складывается из квадратов двух независимых ошибок, растущих с увеличением удаленности снаряда и его скорости на плоскости, ортогональной к лучу зрения перехватывающей батареи:
;
б) желательно сбивать летящий снаряд как можно дальше от защищаемого объекта и соответственно от перехватывающей батареи , чтобы они сами не пострадали от осколков снаряда.
Таким образом, можно надеяться, что даже при некоторой условности предположений о принятом виде весовой функции , она правильно отражает основные особенности задачи.
4. Решение
В то время как для первого игрока (батареи перехвата) задача содержит поиск экстремума функции , непрерывной по всем своим аргументам и лишь условно принятой дискретной для трех выделенных точек, для второго игрока (обстреливающей батареи) она принципиально дискретная из-за выбора одной из двух траекторий. Однако поиск экстремума величины
является весьма громоздким, так как только для поиска точек стационарности по
требуется решать сложные трансцендентные уравнения с полиномами очень высоких степеней относительно времени движения снаряда
.
В точке расположения стреляющей батареи:
=
= 31,8 км;
а) настильная траектория = 30°;
=
= 0,3 км/с;
б) навесная траектория = 60°;
=
= 0,52 км/с.
В точке наивысшего подъема снаряда , где при любом угле
его скорость минимальна и направлена горизонтально:
– высота максимального подъема;
Результаты расчета параметров в точке :
= 16,54 км,
= 0,144 км/с при
= 30° и
= 21,02 км,
= 0,196 км/с при
= 60°.
В точке расположения обстреливаемой цели используем предельное значение величины
при
→0, где время
отсчитывается в обратном направлении, то есть назад от момента расчетного попадания снаряда в объект.
Значения весовой функции при достаточно произвольно заданных коэффициентах
= 300 с и
= 0,1 с/км для трех точек
,
и
(строки) и двух видов траекторий (столбцы) приведены в табл. 1.
Таблица 1 - Значения весовой функции W для трех точек T1, T2 и T3 и двух видов траекторий
Первый игрок | Второй игрок | |
Настильная траектория | Навесная траектория | |
Перехват в точке T1 | 0,463 | 0,167 |
Перехват в точке T2 | 0,339 | 0,35 |
Перехват в точке T3 | 0,181 | 0,399 |
Поэтому смоделируем всю задачу как дискретную для обоих игроков и найдем оптимальные стратегии их поведения в виде решения соответствующей матричной игры с нулевой суммой.
Найдем оптимальные стратегии противников. Стратегией первого игрока называется вектор , где компоненты
– вероятности, с которыми этот игрок (батарея перехвата) выбирает точки перехвата движущегося снаряда.
Аналогично вектор – стратегия второго игрока (обстреливающий противник), где компоненты
– вероятности, с которыми он выбирает траектории снаряда.
Критерий оптимальности: для того чтобы векторы стратегий и
были оптимальными стратегиями соответствующих игроков, а число «Е» было «ценой игры», необходимо и достаточно, чтобы выполнялись неравенства:
, где
= 1,2,3;
= 1,2.
Для решения получившейся матричной игры в соответствии со стандартным методом построим пару двойственных симметричных задач линейного программирования по составленной выше таблице 1 размером 3x2 (матрица «С»).
Задача 1: Найти при условиях:
Задача 2: Найти при условиях:
Здесь от неизвестных вероятностей {} и {
} сделан переход к новым переменным {
} и {
} по правилу:
, где
- «компромиссное» значение искомой величины целевых функций обеих задач (1):
и (2):
, называемое «ценой игры».
Чтобы избежать классического применения громоздкого симплекс-метода, решим задачу (2) графически (рис. 2). Это возможно, поскольку в этой задаче всего два неизвестных. Границы области допустимых значений переменных (область допустимых «планов») выделены жирными отрезками, а вершины – жирными точками. Семейство уровней целевой функции представлено парой менее интенсивных параллельных прямых с указанием градиента
в виде стрелки.
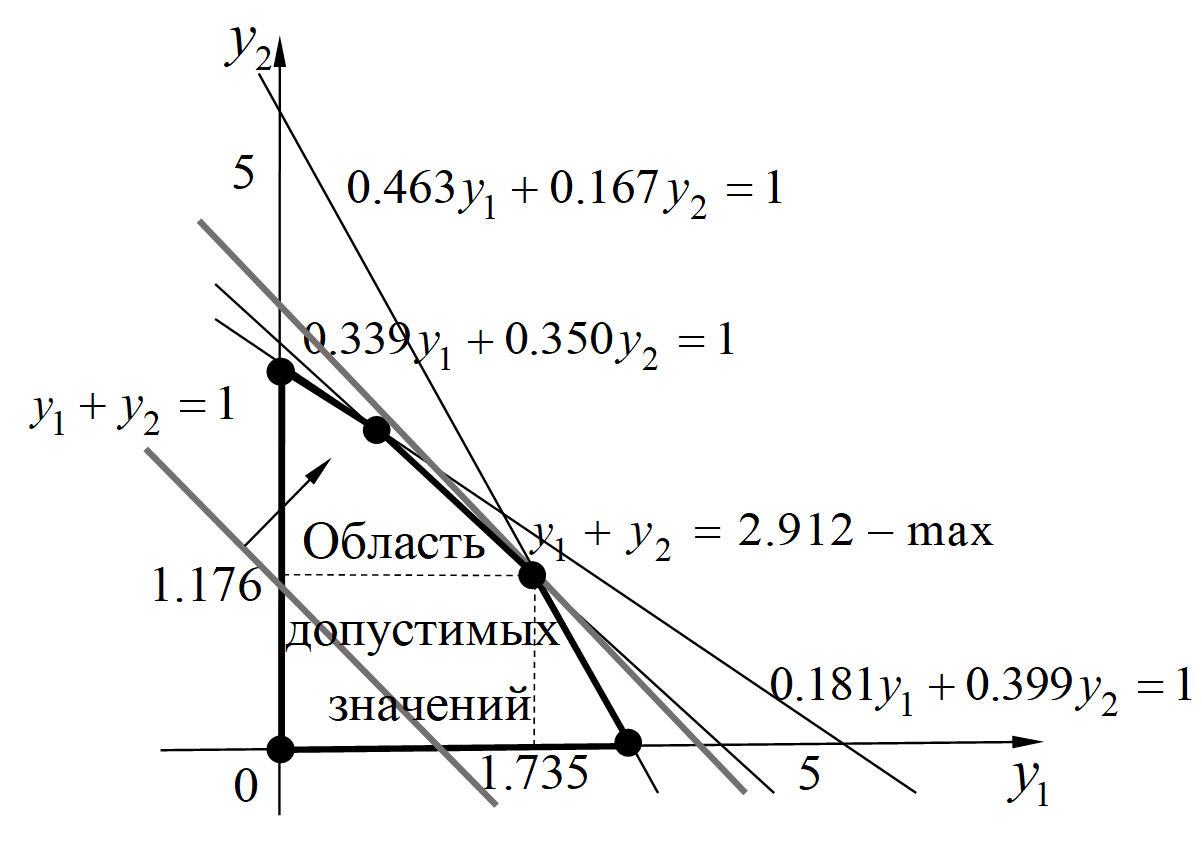
Рисунок 2 - Графическое решение задачи (2) линейного программирования
;
= 0,596;
;
= 0,404.
Оптимальное решение задачи (1) находим, используя двойственность задач и найденное максимальное значение = 2,912.
= 0,109;
= 2,803;
= 0;
;
= 0,037;
;
= 0,963;
;
= 0.
Построение графиков, программирование и основные вычисления выполнялись в математическом пакете MathCAD 15.
5. Обсуждение результатов
Результатом проделанного исследования является:
– в практическом плане: получение распределений вероятностей выбора оптимальных (в смысле игровой задачи) стратегий для атакующей батареи (только в 60% случаев в случайном порядке стрелять по настильной траектории, а в остальных 40% случаев – по навесной траектории) и для обороняющейся батареи (быть готовой в 96% случаев к перехвату в точке максимального подъема снаряда над землей, в 4% в точке
над обстреливающей батареей, но никогда над самой батареей) при некоторых общих условиях на входные параметры задачи;
– в методическом плане: успешное применение модели матричной игры к конкретному актуальному случаю из сравнительно редкой, «нетрадиционной» ситуации артиллерийской дуэли, что, по-видимому, сделано впервые.
Конкретные числа могли измениться при другом виде и параметрах весовой функции , однако на путь решения это принципиально не влияет.
Такая точка зрения на проблему устойчивости полученных результатов основана на том, что при проведении серии полных однотипных расчетов с вариацией каждого из четырех параметров задачи (,
,
,
) в пределах ±10% обнаружились очень малые (в пределах ±1,5%, т.е. в 6 раз меньше для первых трех параметров из них и около 4%, т.е в 2,5 раз меньше для угла
) вариации основных искомых величин (вероятность
, вероятность
– вообще не изменяется).
Оптимальность решения задачи и само его существование рассматриваются в рамках оптимальности решения матричной игры (теорема Дж. Фон Неймана), составляющей основу модели.
Даже если на перехват используется всего одно орудие, то для последующих наибыстрейших перенаводок его следует предварительно навести в точку «ожидания» с удалением от этих трех указанных точек, пропорциональным соответствующим полученным вероятностям. Такие точки «ожидания» можно рассчитать аналитически.
6. Заключение
С помощью модели матричной игры и достаточно общих предположений получены количественные оценки вероятностей оптимальных действий обеих участвующих в артиллерийской дуэли батарей.
