Распространение загрязнения в реках при естественной аэрации
Распространение загрязнения в реках при естественной аэрации
Аннотация
Исследование мотивировано высоким уровнем загрязнения воды в реке Охта и Славянка в Ленинградской области. Для решения проблемы представлена простая математическая модель загрязнения реки и исследовано влияние естественной аэрации на разложение загрязнителя. Модель состоит из пары связанных уравнений диффузии-конвекции для концентраций загрязнителя и растворенного кислорода. Связь этих уравнений определяется реакцией между кислородом и загрязнителем с образованием безвредных соединений. Проведена численная и аналитическая оценка транспортировки загрязняющих веществ в водах реки вдоль её длины (в одном пространственном измерении). В работе рассмотрены разные варианты моделей распространения загрязняющих веществ в водной среде с заданным набором параметров для конкретной реки. Эти параметры соответствуют реальным ситуациям загрязнения рек и могут способствовать принятию адекватных решений при планировании ограничений, налагаемых на источники производственного и бытового загрязнения в сельских и городских районах.
1. Введение
Проблема качества питьевой и других видов воды постоянно возрастает в результате роста численности населения мира и непрерывного повышения промышленной и бытовой деятельности человека [1], [2]. Самоочищение воды речных водоемов от загрязнений происходит за счет сложного комплекса физических, химических и биологических факторов. Это происходит благодаря разбавлению загрязнений большой массой воды, перемешиванию, оседанию взвесей, влиянию солнечного света, аэрация и т.п. В загрязненной реке содержание кислорода в воде сильно уменьшается, поэтому для очистки речных водоемов от бактерий, растворенных органических веществ необходим кислород [3].
При оценке качества воды в реке необходимо учитывать множество факторов: уровень растворенного кислорода; наличие нитратов, хлоридов, фосфатов; уровень взвешенных веществ и т.д. Загрязнители от сельскохозяйственных работ могут вносить значительный вклад в ухудшение качества поверхностных и подземных вод [4], [5].
Существует множество специальных гидротехнических устройств, которые выполняют искусственную аэрацию воды. Но аэрация может происходить естественным способом, за счет соприкосновения воды с атмосферным воздухом. В естественных условиях кислород поступает из атмосферы через водную поверхность (атмосферная аэрация) или образуется в результате жизнедеятельности водных растений (фотосинтетическая аэрация). В этом случае текущая вода поглощает из воздуха кислород, который растворяется в ней. При этом улучшается циркуляция воды внутри водоема, что оказывает благотворное влияние на водную среду, а также значительно уменьшается объем бескислородной области на глубине водоема.
На формирование кислородного режима водоема оказывает влияние много факторов: интенсивность солнечной радиации, фотосинтез фитопланктона и высших растений, степень потребления кислорода в воде гидробионтами, донными отложениями и скорость ветра. В речных водоемах водная поверхность довольно большая, а глубина невелика. Верхние слои реки насыщенны кислородом сильнее, поэтому за счет конвективного переноса постепенно вся толща воды насыщается. Легкое волнение поверхности реки от слабого ветра уже вызывает перемешивание кислорода с водой.
Таким образом, цель настоящей работы состоит в разработке математической модели уменьшения концентрации загрязнителя и повышения растворенного кислорода в условиях естественной аэрации в реке с учетом её течения.
Важным направлением в решении задачи о распространения загрязнений в речной среде является математическое моделирование транспорта загрязняющих веществ [6]. Модельные представления получили широкое распространение для оценки качества воды [7], [8] и для прогнозирования процессов ее очистки [9], [10].
Математические модели оценки качества воды представляются как системы нелинейных дифференциальных уравнений и используются еще с 1920-х годов, например, в 1925 г. известная модель Стритера и Фелпса [11], которая используется для описания баланса растворенного кислорода в реках после попадания загрязняющих веществ. В дальнейшем эта модель была уточнена и в нее вносились различные поправки [12].
Раух и др. [13] математически изучили проблемы загрязнения поверхностных вод, такие как этерификация, острая и хроническая токсичность. Симон и др. [14], [15] представили простую математическую модель загрязнения рек и исследовали влияние аэрации на разложение загрязняющих веществ. Их модель состоит из пары связанных уравнений конвекции-диффузии для загрязняющего вещества и растворенного кислорода. В последнее время были усовершенствованы математические модели загрязнения рек. Хамаунд и др. [16], [17] применили модифицированный метод разложения Лапласа и представили методы решения системы нелинейных интегро-дифференциальных уравнений Вольтера-Фредгольма.
2. Объект и методы
В качестве объекта для исследования были выбраны реки Ленинградской области – Славянка и Охта, имеющие пятый класс опасности. Качество воды реки Славянка послужило мотивом для исследования. Предполагалось, что загрязняющие вещества в основном представляют собой биологические отходы, которые подвергались процессам биодеградации с использованием растворенного кислорода. Пределом допустимого уровня загрязнения воды считалась концентрация растворенного в ней кислорода, не менее 30% от показателя насыщения [18].
Для разработки модели загрязнения воды использовали принцип двух связанных уравнений конвекции-диффузии. Эти два уравнения описывают два процесса: поглощение кислорода из воды, связанное с удалением органических соединений углерода, и поступление кислорода из атмосферы в воду путем аэрации [19], [20]. Для концентраций загрязнителя и растворенного кислорода были выбраны различные параметры источников загрязнения.
В модельных расчетах, представленных в настоящей работе, были рассмотрены скорость течения реки и скорость ветра. Поскольку процессы загрязнения и аэрации являются устойчивыми, мы исследовали возникновение стационарных состояний при удалении загрязнителя аэрацией. Учитывая данные об осадках, скорости течения реки, сброса загрязняющих веществ и др. были построены аналитические и численные решения.
Численное решение системы связанных уравнений конвекции-диффузии, аналитические решения этих уравнений при заданных допустимых условиях и построение графиков проводилась с помощью программного пакета Mathematica 12.3 (Wolfram Research), включающего пакет программ для решения дифференциальных уравнений в частных производных NDSolve и Mass Transfer Model Collection.
3. Описание математических моделей
Изменение концентрации загрязняющих веществ и кислорода рассматривалось вдоль реки, в поперечном направлении концентрация считалась постоянной. Кроме того, такой параметр модели как длина реки L задавался значительно больше, чем её ширина. Поэтому при описании водного потока от истока до устья, течение реки принималось как одномерное, с одним пространственным параметром x(м) вдоль реки. Такое допущение в исходных параметрах модели соответствует критерию Доббинса [21].
Связанность уравнений определяется тем, что кислород реагирует с загрязняющим веществом, образуя безвредные соединения. Принимаем (для упрощения), что диффузия идет в одном направлении и сопровождается вынужденной конвекцией, c концентрацией СХ(x,t) (кг·м–3) для загрязнителя и СО(x,t) (кг·м–3) для растворенного кислорода. Следовательно, для рассмотрения скорости изменения концентрации в зависимости от положения x и времени t (дни), может быть предложена следующая система уравнений:
В уравнение (1) входит слагаемое, описывающее снижение концентрации загрязняющего вещества со скоростью qX·H(x). В уравнении (2), которое описывает массовое содержание растворенного кислорода, учитывается скорость увеличения концентрации кислорода СО до насыщения СS [α·(СS – СО)]. Величина H(x) представляет собой функцию Хэвисайда (H(x) = 1, если x > 0 и 0 во всех остальных случаях). Добавление ее в качестве множителя учитывает то, что загрязняющие вещества сбрасываются только при x ≥ 0.
Связывание уравнений (1 – 2) позволяет определить концентрацию растворенного кислорода СО и концентрацию загрязнителя СХ одновременно. При решении этих уравнений использовался ряд параметров, описывающих экологическую обстановку и геологические характеристики для рек Охта и Славянка (табл. 1).
4. Результаты
Уравнения (1 – 2) решались с использованием граничных условий, соответствующих наличию загрязнений в верхней и нижней частях реки, вдоль её длины. Относительно произвольной точки x на длине реки было выделено два участка. На участках выше (x > L) и ниже (x < L) по течению, в целях упрощения решения задачи, загрязняющие вещества добавлялись с постоянной скоростью qX.
Таблица 1 - Параметры экологической обстановки и геологические характеристики рек Охта и Славянка
Параметр | р. Охта | р. Славянка |
L - длина реки (км) [26] | 90 | 39 |
Dp - коэффициент диффузии загрязнителя (м2·сут-1) [22] | 4,166·106 | |
Dx - коэффициент диффузии растворенного кислорода в (м2·сут-1) [22] | 2,132·106 | |
v - скорость воды (м·сут-1) [26] | 34,2·103 | 21,3·103 |
S - площадь поперечного сечения (м2) [26] | 50 – 275 | 10 – 100 |
q - скорость поступления загрязнителя вдоль реки (кг·м-1 ·сут-1) [25], [26] | 0,06 | 0,08 |
K1 - коэффициент скорости разложения для загрязняющего вещества при 20 °C (сут-1) [23], [24] | 8,27 | 9,14 |
K2 - коэффициент скорости деаэрации для растворенного кислорода при 20 °C (сут-1) [23], [24] | 32,10 | 21,40 |
k - концентрация потребления кислорода при распада загрязнителя (кг·м-3) [23] | 7,1·10–3 | 4,9·10–3 |
α - массоперенос кислорода из воздуха в воду (м2·сут-1) [23], [24] | 22,50 | 19,4 |
СS - концентрация насыщения кислорода (кг·м-3) [23] | 6·10–3 кг/м3 | 7,4·10–3 кг/м3 |
Скорость снижения концентрации загрязняющих веществ СХ в результате биохимической реакции с растворенным кислородом описывается слагаемым «Михаэлис-Ментен» – K1·[СО/(СО+k)]·СХ. Это слагаемое учитывает скорость удаления загрязнений и определяется концентрацией загрязнителя как при высоком, так и низком содержании кислорода. Во втором уравнении коэффициенты соответствующего слагаемого, описывающего уменьшение концентрации растворенного кислорода, различаются из-за разного веса кислорода и загрязнителя, участвующих в реакции.
Также были рассмотрены случаи с и без дисперсии k (либо пренебрежимо малой k ≈ 0). В процессе решения уравнений (1 – 2), в качестве параметров использованы значения: площади поперечного сечения реки S, скорости течения реки v, скорость поступления загрязнителя qX, скорость переноса через поверхность реки кислорода α, концентрация насыщения кислорода СS, коэффициент диффузии загрязнителя DX и растворенного кислорода DO. Эти показатели в расчетах считались постоянными.
5. Аналитические стационарные решения без диффузии
Если пренебречь диффузионными членами, то при таком подходе существуют стационарные решения (1 – 2) и левые части уравнений исчезают. В этом случае можно представить аналитические решения для концентраций загрязняющих веществ СХ(x,t) = СХ,S(x) и кислорода СО(x,t) = СО,S(x). При этом DO = 0, DX = 0. Тогда уравнения (1 – 2) сводятся к
с граничными условиями СХ,S(0) = 0 и СО,S(0) = СS.
Решения уравнений (3 – 4) для концентраций загрязняющих веществCX,S(x,t) и растворенного кислорода СО,S(x,t) вдоль течения реки в интервале времени от 10 до 50 суток приведены на рис. 1 и 2.
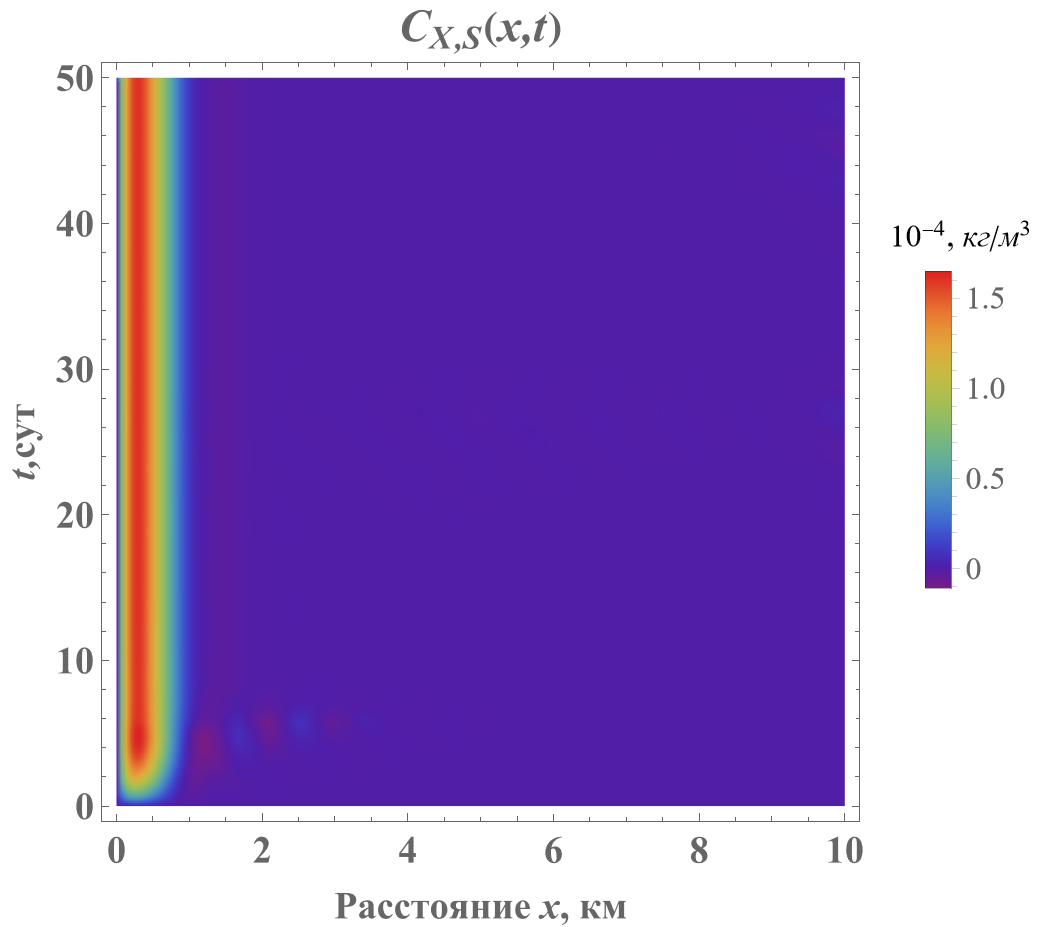
Рисунок 1 - Распределение концентрации загрязнителя CX,S(x,t)·10-4 вдоль реки
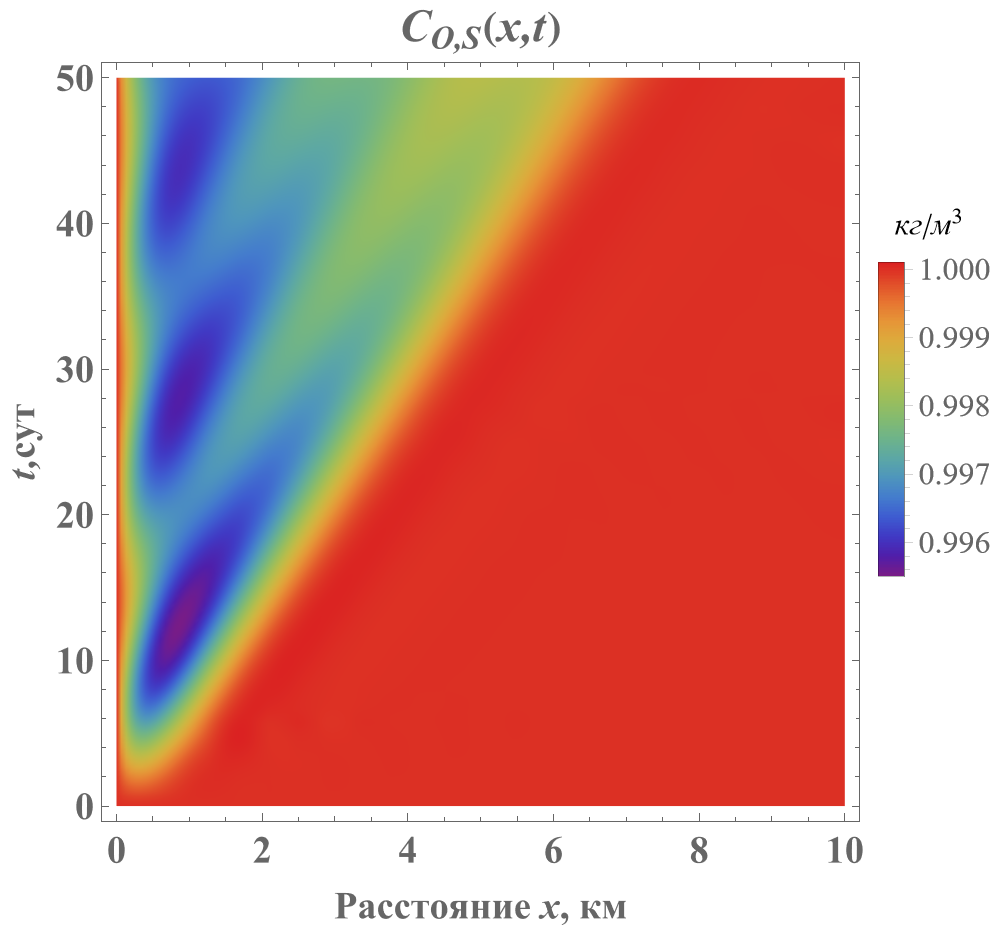
Рисунок 2 - Распределение концентрации СО,S(x,t) растворенного кислорода вдоль реки
Концентрация СХ,S стремится к пределу qX/K1S. Это показано на рисунке 3. Выше по течению нет загрязнения, так как нет рассеивания. Для концентрации растворенного кислорода СО,S решение имеет вид
Ниже по течению уровень кислорода снижается из-за взаимодействия с загрязняющими веществами и концентрация СО,S стремится к пределу СS – qX/K1α. Это показано на рис. 4.
Если загрязняющие стоки в нижнем участке по течению реки, в этой упрощенной модели, таковы, что концентрация растворенного кислорода СО,S составляет не менее 30% значения насыщения СS [18], происходит превышение допустимых норм [26]. Это достигается для уровней qX, которые удовлетворяют qX < 0.7α·K1СS/ K2. В этом случае при наших значениях параметров для рек Охта и Славянка это значение составляет qX < 0.015 кг·м–1·сут–1. (Фактическая скорость поступления загрязняющих веществ в реку Охта и Славянка наблюдается q = 0.06 кг·м–1·сут –1 и q = 0.08 кг·м–1·сут –1 соответственно).
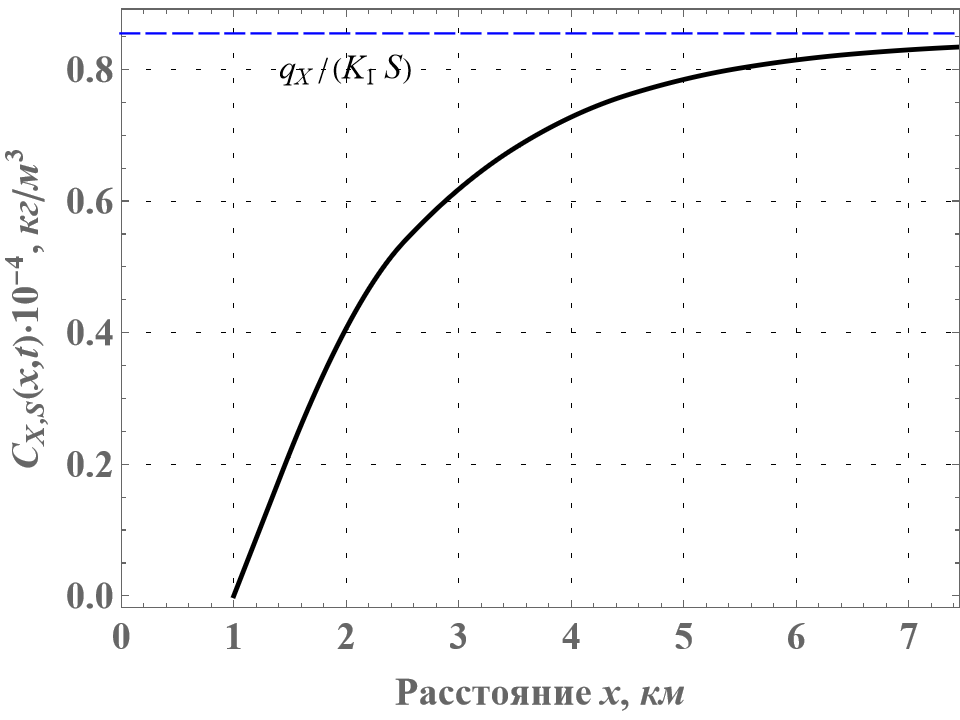
Рисунок 3 - Стационарное решение для СХ,S без дисперсии в случае незначительного k
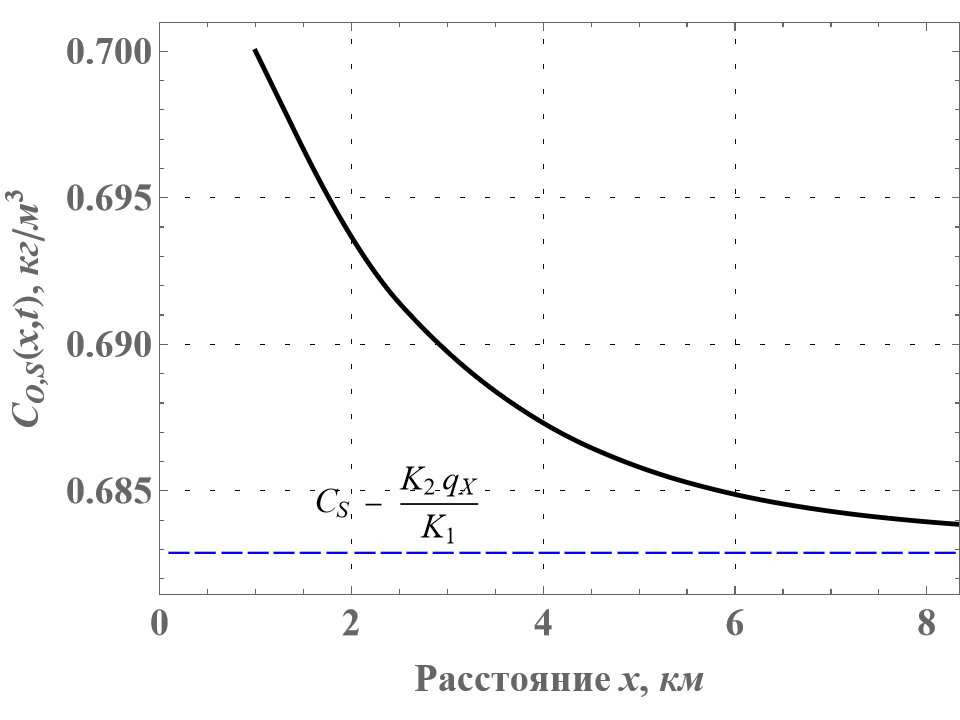
Рисунок 4 - Стационарное решение для СО,S без дисперсии в случае незначительного k
Таким образом, решения для СХ,S и СО,S на больших расстояниях вниз по потоку зависят только от параметров k и qX, что показано на рисунках 3 и 4 пунктирной линией.
6. Модели, включающие диффузию и конвекцию
В этой модели рассмотрен стационарный случай, когда присутствуют члены в уравнении с коэффициентами диффузии (пусть DO ≠ 0, DX ≠ 0), в результате чего сохраняются члены производных второго порядка. Если параметр k считать пренебрежимо малым (k ≈ 0), тогда уравнения (1 – 2) преобразуются следующим образом
В рамках этой модели получается аналитическое решение для концентрации загрязнения СХ,S, которое имеет вид
где c1 = v/2DX и , а для концентрации растворенного кислорода СО,S
где
,
,
,
.
Применяя рассмотренные модели для описания изменения концентраций загрязняющих веществ в реках Охта и Славянка мы рассматривали условия, когда точечных источников загрязнения нет (только распределенные источники). В этом случае СХ,S(x) считались непрерывными, а поступление загрязнителя начиналось с x = 0. В результате концентрация загрязняющих веществ СХ,S(x) имеет относительно плавный характер с разрывом qX/DX·S во второй производной при x = 0.
Если значением параметра k не пренебрегать, и он меняется равномерно, то получается следующая система нелинейных дифференциальных признаков второго порядка:
Граничные концентрации для СХ,S и СО,S на больших расстояниях вниз по течению реки также как СХ,S(-∞) = 0 и СО,S(-∞) = СS. Это позволяет получить простые аналитические решения для соответствующих концентраций:
7. Заключение
Представленные модельные решения показывают, что использование математических моделей транспорта в водной среде реки в случае возникновении разного рода ситуаций, удобно представлять нелинейными дифференциальными уравнениями. В эти уравнения могут быть включены члены, описывающие различные механизмы распространения загрязняющих веществ. Выбор тех или иных механизмов в качестве преобладающих, позволяет упростить модель и получить аналитические решения, в том числе и стационарные. Однако в этом случае не учитываются изменения в концентрации, связанные с вариацией физического состояния (параметров) загрязняющего вещества. Использование таких упрощенных моделей позволяет ввести в них переменные параметры для различных видов поступления загрязняющих веществ.
В модельных расчетах был рассмотрен случай, когда скорость поступления загрязнения q = 0.06 кг·м-1 ·сут-1 (для реки Охта) и q = 0.08 кг·м-1 ·сут-1 (для реки Славянка). Полученные решения показывают, что в водной среде на больших расстояниях в водах реки будут превышены все нормативные показатели и концентрация растворенного кислорода станет ниже предельно допустимого значения [27]. Тем не менее количество загрязняющих веществ, поступающих в эти реки, примерно в 4 раза выше нормы, и это означает, что скорость общего биологического потребления кислорода (БПК) для реки должна составлять не более 5000 кг БПК в сут–1. Однако, исследования показали, что для рек Охта и Славянка такой уровень растворенного кислорода остается выше критического порогового значения – 30% от насыщенного значения. Это, с одной стороны, связано с протяженностью и извилистостью рек, а с другой с небольшой скоростью течения. Критическое значение не достигается в реке Охта из-за конечной длины, на которой фактически не происходит сброс загрязнений в реку Нева.
Представленные модели можно также использовать для определения влияния процессов аэрации на увеличение количества растворенного кислорода в воде, для этого требуется расширение переходной пространственной модели, что не сильно усложнит задачу. Следовательно, предложенные модели могут применяться для принятия решений об ограничении загрязнений рек сельскохозяйственными, промышленными и бытовыми выбросами.
Применение в моделировании разных типов математических моделей дает возможность повысить уровень принятия решений для оценки водных ресурсов. Такие модельные представления позволяют исследовать пространственное и временное распределение концентрации загрязняющих веществ с учетом различных параметров качества воды и источников загрязнения. Упрощенные модели для определённой реальной ситуации помогают принять решения в выборе ограничений, которые будут установлены для снабжения водой сельских и городской регионов.
