ЗАДАЧИ С ПАРАМЕТРАМИ: С ЧЕГО НАЧАТЬ

ЗАДАЧИ С ПАРАМЕТРАМИ: С ЧЕГО НАЧАТЬ

Научная статья

Ледовских И.А.¹, Горбанева Л.В.^2, *, Жулидова Ю.В.³

² ORCID: 0000-0001-9017-823X,

^{1, 2, 3} Тихоокеанский государственный университет, Хабаровск, Россия

* Корреспондирующий автор (largorbaneva[at]mail.ru)

Аннотация

В статье на основании статистики по выполнению заданий с развернутым ответом профильного уровня ЕГЭ по математике и методических рекомендаций для учителей проводится анализ проблем, возникших при решении задач с параметрами, которые являются одними из самых трудных разделов школьной математики. Решение таких задач требует от школьников не только хорошего знания стандартных методов решений уравнений и неравенств, но и умений проводить довольно разветвленные логические построения. Кроме этого, в статье даются рекомендации по некоторым моментам, относящимся к решению задач с параметрами: на что следует обратить внимание при решении таких задач, с чего начать решать уравнение или неравенство, какой метод выбрать, что обязательно необходимо учесть при решении данных задач.

Ключевые слова: задачи с параметрами, методы решения задач с параметрами, статистика выполнения заданий, трудности при решении задач с параметрами, с чего начать решать задачу.

PROBLEMS WITH PARAMETERS: WHERE TO START

Research article

Ledovskikh I.A.¹, Gorbaneva L.V.^2, *, Zhulidova Yu.V.³

² ORCID: 0000-0001-9017-823X,

^{1, 2, 3} Pacific National University, Khabarovsk, Russia

* Corresponding author (largorbaneva[at]mail.ru)

Abstract

The article analyzes the issues encountered in solving problems with parameters, which are among the most difficult sections of school mathematics. The analysis is based on the statistical data on completing advanced tasks of the specialized level (the level for intended STEM majors) of the Unified State Exam (Единый государственный экзамен) in mathematics and methodological recommendations for teachers. Solving such problems requires students not only to have a good knowledge of standard methods for solving equations and inequalities but also the ability to conduct fairly extensive logical constructions. In addition, the article provides recommendations on some points related to solving problems with parameters: what to pay attention to when solving such problems, where to start solving an equation or inequality, which method to choose, and what must be taken into account when solving these problems.

Keywords: problems with parameters, methods for solving problems with parameters, task completion statistics, difficulties in solving problems with parameters, how to start solving the problem.

Введение

Задачи с параметрами входят в ЕГЭ и, являясь одними из самых сложных задач, их решение оценивается достаточно высоко. На самый высший балл (4 балла) оцениваются только две задачи ЕГЭ: задача № 19 (числа и их свойства) и задача № 18 (задача с параметрами). Казалось бы, что школьники должны быть максимально заинтересованы в решении таких задач. Однако, по результатам анализа выполненных экзаменационных работ, участники экзамена показывают низкие результаты.

Если проследить статистику выполнения всех заданий с развернутым ответом профильного уровня по Хабаровскому краю за 2017 – 2019 года, то можно получить следующую картину [4], [5], [6] (см. таблицу 1)

 

Таблица 1 – Статистика выполнения заданий с развернутым ответом профильного уровня ЕГЭ по математике в Хабаровском крае

Задания с развернутым ответом	13	14	15	16	17	18	19
2017 год
% выполнения задания на высший балл	22,4	10	19,4	0,6	3,9	0,2	1,4
% выполнения задания (с учетом частичного выполнения)	28,1	22,2	20,6	2,3	5,7	1,4	23,1
2018 год
% выполнения задания на высший балл	17,4	4,4	14,9	0,3	0,4	0,1	0,1
% выполнения задания (с учетом частичного выполнения)	21,9	10,4	16,3	3,8	1,2	1,1	4,1
2019 год
% выполнения задания на высший балл	30,9	0,6	11,6	0,7	6,9	0,8	0,1
% выполнения задания (с учетом частичного выполнения)	36,2	7,2	13,7	1,8	8,6	2,7	7,4

 

Из данных таблицы видно, что выполняемость заданий по данной теме в 2017 – 2019 годах составила не более 3%.

Если проанализировать методические рекомендации для учителей, подготовленных на основе анализа типичных ошибок участников ЕГЭ по математике, то можно проследить статистику выполнения заданий с развернутым ответом профильного уровня ЕГЭ по математике по всей России и увидеть следующую картину: выполняемость заданий по данной теме составляет не более 5 %, что также является одним из низких результатов среди других показателей (сравниваются показатели выполнения заданий с развернутым ответом). И здесь идет речь не просто о решении всего задания в целом, а даже о его частичном выполнении, то есть получении «ненулевых баллов» [10].

Основные результаты

При решении задач такого рода можно отметить следующие трудности, с которыми сталкиваются участники экзамена [6], [10]:

• приходится производить ветвление всех значений параметров на отдельные классы;
• зачастую школьники не умеют переводить задачу, заданную аналитически, в графическую;
• сложно воспринимаются формулировки самих заданий.

К сожалению, в учебной литературе наблюдается некоторый дефицит объяснений по решению задачам с параметрами. Соответствующая литература существует и даже весьма многочисленная. Но выпускаемые книги, задачники и методические пособия на эту тему нередко имеют очень узкую направленность или ориентированы на уже подготовленного школьника. Да и в программах по математике задачам с параметрами либо практически вообще не отводится места, либо рассматривается узкий круг задач, либо их изучение затрагивается лишь в 11 классе. Между тем, такие задачи не просто можно, а даже необходимо изучать, начиная с линейных уравнений, то есть с 7 класса [9].

Важно, чтобы школьники уже с самого начала осознали и понимали несколько важных моментов:

• Параметр имеет двойную природу: с одной стороны – это число, с другой стороны – неизвестная).

Например, рассмотрим следующее задание: сравните числа -а и 3а.

Решение:

Самая распространенная ошибка, считать, что -а меньше 3а, так как на первый взгляд кажется, что число -а является отрицательным, а 3а – положительным. Но это не совсем так. Сам по себе параметр а может принимать любое из трех значений: a > 0, a = 0 и a < 0. Значит, необходимо рассмотреть все три случая:

1) если a > 0, то -а действительно является отрицательным, а 3а – положительным числом, а значит -а меньше 3а.

2) если a = 0, то -a = 0 и 3a = 0, а значит они равны между собой.

3) если a < 0, то -а становится положительным, а 3а – отрицательным числом, а значит -а больше 3а.

Ответ: если a > 0, то -a  < 3a; если a = 0, то -a  = 3a; если a < 0, то 3a < -a.

• Научились составлять особую запись ответа, существенно отличающуюся от записи ответа, который получаем при решении уравнений и неравенств без параметра.

Например: решите уравнение .

Решение:

Видно, что x = a – единственный корень заданного уравнения. Однако этот результат – еще не ответ.

Как уже отмечалось ранее, помимо привычного нахождения ответа, необходимо еще установить наличие и недопустимость значений параметра а.

Условие  как раз и получим такое недопустимое значение, а именно требование . И тогда ответ примет вид:

Ответ: если , то ; если , то нет решений.

• В некоторых случаях учитывали независимость параметра от условия задачи.

Так, например, левая часть уравнения  неотрицательна, но это не означает, что выражение  не может быть неотрицательным. А вот если , то мы в любом случае получим, что уравнение решений не имеет.

Таким образом, встает необходимость рассмотрения не только основных и наиболее популярных типов задач с параметрами, но и изучить другие приемы и методы их решений, а также затронуть и нестандартные подходы к решению таких задач.

Так каков же первый шаг. С чего начать?

Первое что необходимо – это четко определить, что из себя представляет заданное уравнение.

Иногда задачу с параметром формулируют в несколько ином виде: решить семейство уравнений, получаемых из уравнения при любых действительных значениях параметра.

Очевидно, что выписать каждое такое уравнение из бесконечного семейства уравнений представляет довольно громоздкую задачу. Сделать это все же можно, разделив все множество значений параметра на несколько подмножеств, а затем решить заданное уравнение на каждом из этих подмножеств.

Для этого необходимо выделить так называемые контрольные значения параметра, при которых происходят качественные изменения уравнения. Например, в уравнении  контрольным значением параметра а служит значение .

Обращаем так же внимание на то, что в рассмотренных выше примерах областью допустимых значений для параметра являлось все множество вещественных чисел. Разумеется, что примерам иного рода также следует уделять внимание.

Вот лишь несколько уравнений, где необходимо учитывать область допустимых значений не только переменной х, но и самого параметра а:

 

Основные методы решения задач с параметром

Выделяют несколько методов. Коротко рассмотрим некоторые из них [1], [7], [11].

Самый распространенный метод – это так называемый метод «решения в лоб», когда повторяются все стандартные процедуры решения задач без параметра.

Однако здесь есть моменты, на которые следует обратить внимание:

• установить наличие контрольных значений параметра;
• учесть область допустимых значений как самой переменной, так и параметра;
• выявить значения параметра, которые могут привести заданное выражение к тождественно истинному или тождественно ложному выражению.

Пример: решите уравнение .

Решение:

На первый взгляд кажется, что уравнение не имеет корней только при условии, что знаменатель обратится в ноль, то есть только при .

Но, положим  и преобразуем исходное уравнение, перенеся все слагаемые в левую часть и приведя к общему знаменателю:

Умножим обе части уравнения на  и выразим .

Получаем, что выражение  не имеет смысла при .

Тогда ответом будет следующая запись: если  и , то ; если и , то уравнение не имеет корней.

Таким образом, с одной стороны, многим школьникам близок аналитический метод, так как они в достаточной степени владеют различными приемами решения уравнений и неравенств. С другой стороны, решая задачу таким способом, можно получить громоздкое решение, требующее большой внимательности и высокой математической грамотности.

Следующим по популярности методом является графический метод.

В зависимости от роли параметра, выделяют два основных графических приема построения графического образа: первый – на координатной плоскости , второй – на .

При этом важно помнить, что не все задачи могут быть решены графическим методом, так как данный метод не является универсальным. Лучше всего решаются задачи на нахождение количества решений, так как на «языке» графиков количество корней – это количество точек пересечения (или их отсутствие) графиков функций [1], [7], [9].

Несмотря на исключительную наглядность, применение графического метода требует от учеников умения проводить построения различных графиков, а иногда и вести целые графические исследования. Здесь важно понимать, какие графики могут получаться, или как, в зависимости от значений параметра, будет изменяться построенный график.

Так, например, можно сказать, что уравнение  задает множество всех прямых, которые проходят через начало координат. Однако среди всех таких прямых все же существует прямая, которая проходит через начало координат, но не удовлетворяет условию, и это прямая, совпадающая с осью Оу, уравнение которой имеет вид .

Рассмотрим следующий пример: Найдите значения параметра a, при которых уравнение  имеет ровно три различных корня.

Решение:

Если эту задачу решать аналитически, то решение будет довольно-таки громоздким и требовать большой внимательности, так как придется не просто решить два уравнения , но и учесть возможность совпадения полученных корней.

А вот если задачу перевести на графический язык, то все становится наглядным и простым.

На координатной плоскости  уравнение  задает параболу, а уравнение  – ломаную линию.

Построим графики этих функций (см. рисунок 1):

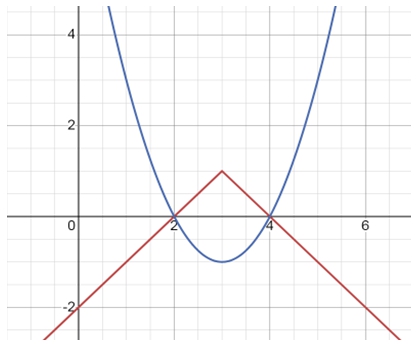
Рис. 1 – Графики функций

 

Из графика видно, что уравнение имеет три различных корня только при двух значениях .

Но не стоит ограничивать себя изучением только одного или двух методов решения задач. Всегда выгоднее иметь в запасе не один, а несколько методов или приемов. Кроме того, при решении задач можно комбинировать разные методы [2], [3], [9].

Среди таких методов можно выделить:

• решение относительно параметра;
• поиск свойств функций (например, четность или нечетность, монотонность, экстремальные свойства функции);
• поиск «выгодной точки»;
• оценка (например, поиск наименьших или наибольших значений функции).

Вот пример такой задачи.

Пример: При каких значениях параметра а уравнение  имеет единственное решение.

Решение:

Способ 1. Квадратное уравнение  имеет единственное решение, если его дискриминант  равен нулю. Решив уравнение , получаем .

Способ 2. Введем функцию . Эта функция является квадратичной и задает на плоскости параболу. Если уравнение имеет корни, значит ее график должен пересекать ось абсцисс. Парабола будет иметь только одну точку пересечения с осью абсцисс, если ее вершина лежит на ней, то есть . Получаем: ,

.

Ответ: .

Заключение

Так с чего начать решать задачу? Попробуйте задать себе такие вопросы:

1. Какое уравнение дано в задаче (линейное, квадратное, рациональное или относящееся к другому классу)? Определив тип уравнения, можно попробовать решить задачу, применив к ней известные механизмы решения.
2. Что требуется найти в задаче (решить уравнение или найти количество его корней)? Если, например, требуется найти количество корней, то большинство задач решается графическим методом.
3. Можно ли сразу выделить контрольные значения параметра? Например, для квадратичных уравнений необходимо учитывать старший коэффициент и дискриминант.
4. Если найти область допустимых значений переменной, то повлияет ли это на параметр? Например, в дробных выражениях необходимо учитывать знаменатель, но если знаменатель содержит параметр, то найденные ограничения распространятся и на параметр.
5. Если переменную и параметр «поменять ролями», станет ли от этого проще задача? Может оказаться так, например, что уравнение относительно переменной является квадратичным, а относительно параметра – линейным.

Конечно, на этом весь перечень вопросов, которые можно сформулировать для себя, не заканчивается и его можно продолжать и продолжать. Но от ответа даже на эти вопросы уже будет зависеть дальнейший характер решения.

Конфликт интересов Не указан.

Conflict of Interest None declared.

 

Список литературы / References

1. Горнштейн П.И. Задачи с параметрами / П.И. Горнштейн, В.Б.Полонский, М.С.Якир. – М.: Илекса; Харьков: Гимназия, 2005. – 328 с.
2. Дятлов В.Н. Технологии решения задач: Лекция 2. Общие методы анализа уравнений и неравенств. Уравнения с радикалами / В.Н. Дятлов // Математика. – 2012. – № 6. – С. 46–52.
3. Дятлов В.Н. Технологии решения задач: Лекция 7. Задачи с параметрами. Основные понятия. Уравнения с параметрами / В.Н. Дятлов // Математика. – 2012. – № 11.
4. Итоги проведения государственной итоговой аттестации в Хабаровском крае – Хабаровск: КГКУ РЦОКО, 2017 [Электронный ресурс] URL: https://rcoko.khb.ru/gia-11/stat-ege/stat-2017/ (дата обращения 07.10.2020)
5. Итоги проведения государственной итоговой аттестации в Хабаровском крае – Хабаровск: КГКУ РЦОКО, 2018 [Электронный ресурс] URL: https://rcoko.khb.ru/gia-11/stat-ege/stat-2018/ (дата обращения 07.10.2020)
6. Итоги проведения государственной итоговой аттестации в Хабаровском крае – Хабаровск: КГКУ РЦОКО, 2019 [Электронный ресурс] URL: https://rcoko.khb.ru/gia-11/stat-ege/stat-2019/ (дата обращения 07.10.2020)
7. Козко А. И. Задачи с параметром и другие сложные задачи / А.И.Козко, В.Г. Чирский. – М.: МЦНМО, 2007. – 296 с.
8. Методы решения задач с параметрами [Электронный ресурс] URL: https://clck.ru/RvJUi (дата обращения 07.10.2020).
9. Прокофьев А.А. Задачи с параметрами / А.А.Прокофьев. – М.: МИЭТ, 2004. – 258 с.
10. ФИПИ: Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2019 года по математике [Электронный ресурс] URL: http://fipi.ru/ege-i-gve-11/analiticheskie-i-metodicheskie-materialy (дата обращения 07.10.2020).
11. Шахмейстер А.Х. Уравнения и неравенства с параметрами / А.Х.Шахмейстер – 4-е изд. – СПб.: «Виктория плюс»: М.: МЦНМО: СПб.: «Петроглиф», 2019. – 304 с.

Список литературы на английском языке / References in English

1. Gornstein P.I. Zadachi s parametrami [Problems with parameters] / P.I. Gornstein, V.B. Polonsky, M.S. Yakir. – M.: Ileksa; Kharkov: Gymnasium, 2005. – 328 p. [in Russian]
2. Dyatlov V.N. Tehnologii reshenija zadach: Lekcija 2. Obshhie metody analiza uravnenij i neravenstv. Uravnenija s radikalami [Problem solving technologies: Lecture 2. General methods for analyzing equations and inequalities. Equations with radicals] / V.N. Dyatlov // Matematika [Mathematics]. – 2012. – No. 6. – P. 46-52. [in Russian]
3. Dyatlov V.N. Tehnologii reshenija zadach: Lekcija 7. Zadachi s parametrami. Osnovnye ponjatija. Uravnenija s parametrami [Problem solving technologies: Lecture 7. Tasks with settings. Basic concepts. Equations with parameters] / V.N. Dyatlov // Mathematics. – 2012. – No. 11. [in Russian]
4. Itogi provedenija gosudarstvennoj itogovoj attestacii v Habarovskom krae [Results of the state final certification in the Khabarovsk Territory] – Khabarovsk: KGKU RTSOKO, 2017 [Electronic resource] URL: https: // rсoko.khb.ru/gia-11/stat-ege/stat-2017 / (accessed 07.10.2020) [in Russian]
5. Itogi provedenija gosudarstvennoj itogovoj attestacii v Habarovskom krae [Results of the state final certification in the Khabarovsk Territory] – Khabarovsk: KGKU RTSOKO, 2018 [Electronic resource] URL: https: // rсoko.khb.ru/gia-11/stat-ege/stat-2018 / (accessed 07.10.2020) [in Russian]
6. Itogi provedenija gosudarstvennoj itogovoj attestacii v Habarovskom krae [Results of the state final certification in the Khabarovsk Territory] – Khabarovsk: KGKU RTSOKO, 2019 [Electronic resource] URL: https:// rсoko.khb.ru/gia-11/stat-ege/stat-2019 / (accessed 07.10.2020) [in Russian]
7. Kozko A.I. Zadachi s parametrom i drugie slozhnye zadachi [Problems with a parameter and other complex problems] / A.I. Kozko, V.G. Chirsky. – M.: MTSNMO, 2007. – 296 p. [in Russian]
8. Metody reshenija zadach s parametrami [Methods of solving problems with parameters] [Electronic resource] URL: https://infourok.ru/metody_resheniya_zadach_s_parametrami-398722.htm (accessed 07.10.2020.). [in Russian]
9. Prokofiev A.A. Zadachi s parametrami [Problems with parameters] / A.A. Prokofiev. – M.: MIET, 2004. – 258 p. [in Russian]
10. FIPI: Metodicheskie rekomendacii dlja uchitelej, podgotovlennye na osnove analiza tipichnyh oshibok uchastnikov EGJe 2019 goda po matematike [FIPI: Methodological recommendations for teachers, prepared on the basis of an analysis of typical errors of 2019 exam participants in mathematics] [Electronic resource] URL: http://fipi.ru/ege-i-gve-11/analiticheskie-i-metodicheskie-materialy (accessed 07.10.2020.). [in Russian]
11. Shahmeister A.H. Uravnenija i neravenstva s parametrami [Equations and inequalities with parameters] / A.H. Shahmeister – 4th ed. – St. Petersburg: "Victoria Plus": M.: MTSNMO: St. Petersburg: "Petroglyph," 2019. – 304 p. [in Russian]