СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ ЗАДАЧИ КОШИ ДЛЯ ШИРОКОГО КЛАССА ЭРЕДИТАРНЫХ ОСЦИЛЛЯТОРОВ

Паровик Р.И.

ORCID: 0000-0002-1576-1860, Кандидат физико-математических наук,

Институт космофизических исследований и распространения радиоволн ДВО РАН,

Камчатский государственный университет имени Витуса Беринга

Работа выполнена по государственному заданию, НИР КамГУ им. Витуса Беринга «Применение дробного исчисления в теории колебательных процессов» №AAAA-A17-117031050058-9.

СУЩЕСТВОВАНИЕ И ЕДИНСТВЕННОСТЬ ЗАДАЧИ КОШИ ДЛЯ ШИРОКОГО КЛАССА ЭРЕДИТАРНЫХ ОСЦИЛЛЯТОРОВ

Аннотация

В настоящей работе с помощью элементов теории функционального анализа (теоремы о неподвижной точке) обосновывается существование и единственность задачи Коши для специального класса интегро-дифференциальных уравнений с разностными ядрами в виде степенных функций. Исходное интегро-дифференциальное уравнение с помощью производных дробного порядка в смысле Герасимова-Капуто сводилось к уравнению, которое описывает широкий класс фрактальных осцилляторов или осцилляторов с памятью.

Ключевые слова: эредитарность, принцип сжимающего отображения, существование и единственность решения, задача Коши, фрактальный осциллятор.

Parovik R.I.

ORCID: 0000-0002-1576-1860, PhD in Physics and Mathematics,

Institute of Cosmophysical Research and Radio Wave Propagation, FEB RAS,

Kamchatsky State University named after Vitus Bering

EXISTENCE AND UNIQUENESS OF THE CAUCHY PROBLEM FOR A WIDE CLASS OF EREDITARY OSCILLATORS

Abstract

In this paper, using the elements of the theory of functional analysis (fixed-point theorem), the existence and uniqueness of the Cauchy problem for a special class of integral and differential equations with difference kernels in the form of power functions is justified. The initial integral and differential equation with the help of derivatives of fractional order in the sense of Gerasimov-Caputo is reduced to an equation, describing a wide class of fractal oscillators or oscillators with memory.

Keywords: heredity, contraction mapping principle, existence and uniqueness of a solution, the Cauchy problem, the fractal oscillator.

Введение. В одной из глав монографии [1], посвященной эредитарным процессам, был приведен эредитарный осциллятор, который исследовал Вито Вольтерра. В его работах [2,3], было впервые также введено понятие эредитарности, означающее эффект памяти или последействия и заключающееся в зависимости текущего состояния, рассматриваемой динамической системы от предыдущих состояний, т.е. от предыстории.  С точки зрения математики эредитарный осциллятор можно описать с помощью интегро-дифференциального уравнения с разностным ядром, которое называют функцией памяти.

Функция памяти может принимать любой вид, который определяется условиями рассматриваемой задачи. Существуют два предельных случая: отсутствие памяти и ее полное наличие. Первому случаю соответствует функция памяти, взятая в виде дельта-функции, а второму – функция Хевисайда. Промежуточные функции памяти, определяют динамические системы с частичной потерей памяти так, как текущие их состояния будут зависеть лишь от конечного числа предыдущих состояний. Отметим, что наличие в природе степенных законов и фракталов [4], позволяют предположит степенной вид функции памяти [1]. Необходимо отметить, что степенная функция памяти дает возможность перехода от модельного интегро-дифференциального уравнения к модельному уравнению с производными дробных порядков, которые изучаются в рамках дробного исчисления [1], [5], [6]. Тогда модельное уравнение будет описывать один достаточно широкий класс эредитарных осцилляторов – фрактальные осцилляторы. Исследованию некоторых фрактальных осцилляторов были посвящены работы [7-21]. Более полно, на наш взгляд, они были изучены в монографиях [22], [23], но тем ни менее многие вопросы в этих работах были оставлены без должного внимания. Одним из таких вопросов, например, является вопрос о существовании и единственности решения задач Коши. Поэтому эта работа посвящена обоснованию существования и единственности задачи Коши для целого класса фрактальных осцилляторов.

По аналогии с работой [24] мы сначала дадим ряд определений, которые будем использовать при доказательстве основной теоремы.

Определение 1. Функция действительного переменного ,  принадлежит пространству , если существует такое , что , где   и  пространству , если .

Определение 2. Интеграл Римана-Лиувилля порядка  для функции  имеет вид:

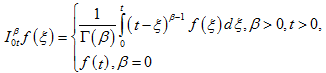                                                  (1)

Определение 3. Производная дробного порядка β в смысле Герасимова-Капуто для функции  является оператор  [25, 26]:

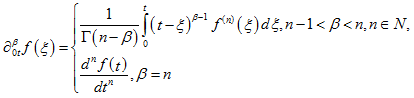                                         (2)

Отметим свойство композиции операторов (1) и (2);

                                                           (3)

Более детально о свойствах операторов (1) и (2) можно узнать в работах [1, 5, 6].  Рассмотрим следующую задачу Коши:

                    (4)

где ,  - время процесса,  - заданные константы,  имеет смысл коэффициента трения, функция  непрерывная функция, такая что   - пространство Банаха.

Задача Коши (4) в зависимости от вида функции   характеризует два класса фрактальных осцилляторов. В случае, если функция  является линейной, то мы приходим к классу линейных фрактальных осцилляторов, некоторые из них были рассмотрены в работе [23]. Другой класс фрактальных осцилляторов мы получим, если функция  будет нелинейной. Такой класс характеризует нелинейные фрактальные осцилляторы [22].

Введем пространство всех непрерывных функций, определенных на  порожденное нормой , которое обозначим .

Лемма. Для задачи Коши (4) справедлива формула:

                   (5)

Действительно.  Из уравнения (4) мы имеем:

                                                            (6)

Учитывая свойство (3), уравнение (6) можно записать в виде:

                                                                     (7)

Действуя на правую и левую части уравнения (7) оператором  и дважды интегрируя от 0 до , мы получим решение:

                                                           (8)

При  согласно начальным условиям (5),  мы получим, что константы интегрирования в (8) определены как .  Откуда следует соотношение (5). Лемма доказана.

Определим оператор  такой, что

                  (9)

где .

Докажем существование и единственность задачи Коши (4), используя принцип сжимающих отображений (теорема Банаха о неподвижной точке).

Определим условия:

1. Функция 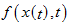 удовлетворяет по  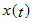условию:

                                              (10)

2. Пусть существуют два положительных действительных числа 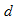 и 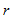 таких , что  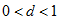и выполнено условие:

                                           (11)

где .

Теорема.  Решение задачи Коши (4) существует и единственно в пространстве  , если выполнены условия (10) и (11).

Доказательство. Докажем, что оператор (9) имеет фиксированную точку в шаре . Пусть , тогда для оператора (9) можно записать соотношение:

или мы приходим к следующему неравенству:

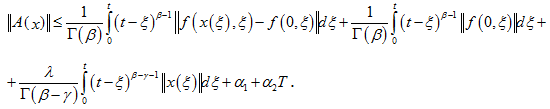
Далее с учетом условия (10) при y=0, имеем:

а с учетом условия (11) окончательно получим неравенство:

из которого следует включение . Следовательно, оператор (9) отображает  в себя.

Покажем, что оператор (9) является сжимающим отображением в шаре . Пусть 

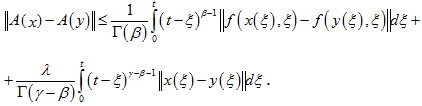
С учетом условия (11), имеем:

Отсюда следует, что оператор (9) является сжимающим, поэтому имеет единственную неподвижную точку, которая является решением задачи Коши (4). Теорема доказана.

Заметим, что если обобщить уравнение (4) на случай переменных дробных порядков  и  в виде:

то будет затруднительно получить общее решение в виде соотношения (5), так как нарушается свойство композиции операторов:  и поэтому существуют определенные трудности в применении принципа сжимающих отображений. В этом случае возникает задача о выборе определения производных дробных переменных порядков [27].

Заключение. В этой работе была доказана теорема о существовании и единственности задачи Коши (4), однако интерес может представлять более общая задача Коши:

               (12)

Задача Коши (12) описывает более широкий класс фрактальных осцилляторов, чем задача Коши (4). Например, в случае, когда функция   четна, а функция нечетна, то мы получаем обобщенное уравнение Льенара, которое характеризует фрактальные автогенераторы типа Ван дер Поля [28], Ван дер Поля-Дуффинга [29], ФитцХью-Нагумо [30] и др., часто встречающиеся в различных приложениях физики, техники, биологии и других науках.

Список литературы/References

1. Uchaikin V. V. Fractional derivatives for physicists and engineers. Volume I. Background and theory / Uchaikin V.V. – Berlin: Springer, 2013. – 373 p.
2. Volterra V. Sur les equations integro-differentiellesetleurs applications / Volterra V // Acta Mathematica. – 1912. – 35. –  no 1. – P. 295 – 356.
3. Volterra V. Theory of Functionals and of Integral and Integro-differential Equations / Volterra V.  –  New York:  Dover Publication Inc, 2005. – 226 p.
4. Schroeder M. Fractals, chaos, power laws: minutes from an infinite Paradise / Schroeder M. – New York: V.H. Freeman, 1991.
5. Kilbas A.A. Theory and Applications of Fractional Differential Equations / Kilbas A.A., Srivastava H.M., Trujillo J.J.  – North-Holland. Amsterdam. Elsevier. 2006. – 541 p.
6. Oldham K. B. The fractional calculus. Theory and applications of differentiation and integration to arbitrary order / Oldham K. B., Spanier J. – London: Academic Press, 1974. – 240 p.
7. Mainardi F. Fractional Relaxation-Oscillation and Fractional Diffusion-Wave Chaos / Mainardi F. // Soliton & Fractal. – 1996. – vol. 7. – no. 9. – P. 146 – 1477.
8. Meilanov R.P. Features of the phase trajectory of a fractal oscillator / Meilanov R.P., Yanpolov M.S. // Technical Physics Letters. – 2002. – vol. 28. – no. 1. – P. 30 – 32.
9. Achar B.N.N. Response characteristics of a fractional oscillator / Achar B.N.N., Hanneken J.W., Clarke T. // Physica A. – 2002. – vol. 309. – no. 3-4. – P. 275 – 288.
10. Al-Rabtah A. Solutions of a fractional oscillator by using differential transform method / Al-Rabtah A., Erturk V. S., Momani S. // Computers & Mathematics with Applications. – 2010. – vol. 59. – no. 3. – P. 1356 – 1362.
11. Afanas'ev V.V. Polish Stabilization of the Inertial E_ects of the Fractal Oscillator / Afanas'ev V.V., Daniel M.J.E. // Technical Physics Letters. – 2010. – vol. 36. – no. 7.  1 – 6.
12. Zurigat M. Solving Fractional Oscillators Using Laplace Homotopy Analysis Method / Zurigat M. // Annals of the University of Craiova, Mathematics and Computer Science Series. – 2011. – vol. 38(4). – P. 1 – 11.
13. Parovik R.I. Fractal parametric oscillator as a model of a nonlinear oscillation system in natural mediums / Parovik R.I.  // International Journal of Communications, Network and System Sciences. – 2013. – vol. 6. – no 3. –  134 – 138.
14. Zaitsev V.V. Self-oscillations dynamics of active fractional oscillator / Zaitsev V.V., Karlov Ar.V., Yarovoy G.P. // Theoretical Physics. – 2013. – vol. 14. – P. 11 – 18.
15. Xu Y. Models and numerical solutions of generalized oscillator equations / Xu Y., Agrawal O.P. // Journal of Vibration and Acoustics. – 2014. – vol. 136. – 051005.
16. Syta A. Chaotic vibrations of the Du_ng system with fractional damping / Syta A., Litak G., Lenci S., Schefer M. // Chaos: An Interdisciplinary Journal of Nonlinear Science. – 2014. – vol. 24. – issue 1. –
17. Blaszczyk T. A numerical solution of a fractional oscillator equation in a non-resisting medium with natural boundary conditions / Blaszczyk T. // Romanian Reports in Physics. – 2015. – vol. 67. –  2. – P. 350 – 358.
18. Parovik R.I. Mathematical modeling of nonlocal oscillatory Duffing system with fractal friction / Parovik R.I. // Bulletin KRASEC. Physical and Mathematical Sciences. – 2015. – vol. 10. – issue 1. – P. 16 – 21.
19. Parovik R.I. Mathematical modeling of the hereditary oscillator / Parovik R.I. // Computer Research and Modeling. – 2015. – vol. 7(5). –  1001 – 1021.
20. Parovik R. On a credit oscillatory system with the inclusion of stick-slip / Parovik R. // E3S Web of Conferences. – 2016. – vol. 11. – 00018.
21. Parovik R.I. Mathematical Modelling of Hereditarity Airy Oscillator with Friction / Parovik R.I. // Bulletin of South Ural State University. Series Mathematical Modelling, Programming & Computer Software. – 2017. –vol. 10. – no 1. – P. 138–148.
22. Petras I. Fractional-Order Nonlinear Systems. Modeling, Analysis and Simulation / Parovik R.I. – Beijing and Springer-Verlag Berlin Heidelberg: Springer, 2011. – 218 p.
23. Parovik R.I. Mathematical modeling of hereditary linear oscillators/ Parovik R.I . – Petropavlovsk-Kamchatsky: Vitus Bering Kamchatka State University. 2015. – 178 p.
24. Anber A. New existence and uniqueness results for fractional differential equations / Anber A., Belarbi S., Dahmani Z.  // Analele Universitatii "Ovidius" Constanta - Seria Matematica. – 2013. – vol. 21(3). – P. 33 – 41.
25. Gerasimov A.N. Generalization of linear deformation laws and their application to internal friction problems / Gerasimov A.N. // AS USSR. Applied mathematics and mechanics. – 1948. – vol. 12. – P. 529 – 539.
26. Caputo M. Linear models of dissipation whose Q is almost frequency independent-II / Caputo M. // Geophysical Journal International. – 1967. – vol. 13. – no. 5. – P. 529 – 539.
27. Samko S.G. Fractional integration and differentiation of variable order / Samko S.G. // Analysis Mathematica. – 1995. – vol. 21. – P. 213 – 236.
28. Parovik R.I. Fractional calculus in the theory of oscillatory systems / Parovik R.I. // Modern science-intensive technologies. – 2017. – №1. – P. 66 – 68.
29. Lipko O.D. Mathematical model of propagation of nerve impulses with regard hereditarity / Parovik R.I. // Bulletin KRASEC. Physical and Mathematical Sciences. – 2017. – vol. 17. no 1. – P. 33 – 43.
30. Novikova E.R. Van der Pol-Duffing oscillator with the effect of hereditary. / Novikova E.R. // Bulletin KRASEC. Physical and Mathematical Sciences. – 2017. – vol. 17. – no 2. – P. 65 – 75.