ПРИМЕНЕНИЕ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ К ЗАДАЧАМ АЛГЕБРЫ ЛОГИКИ

Сдвижков О.А.

 Кандидат физико-математических наук, доцент, Российский государственный университет туризма и сервиса

ПРИМЕНЕНИЕ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ К ЗАДАЧАМ АЛГЕБРЫ ЛОГИКИ

Аннотация

В статье с помощью линейного программирования находятся существенные переменные булевых функций, а также проверяются булевы функции на монотонность и линейность.

Обобщается задача о кратчайшем покрытии булевой матрицы, как задача о кратчайшем покрытии булевой матрицы с заданным дефектом. Обобщенная задача о кратчайшем покрытии сводится к задаче линейного программирования, как следствие получается задача линейного программирования, к которой сводится классическая задача о кратчайшем покрытии булевой матрицы.

Приведены примеры, в которых задачи теории булевых функций решаются с помощью линейного программирования.

Ключевые слова: оптимизация, булева функция, монотонность, линейность, кратчайшее покрытие.

 

Sdvizhkov O.A.

PhD in Physics and Mathematics, Associate Professor, Russian State University of Tourism and Service

APPLICATION OF LINEAR PROGRAMMING TO THE TASKS OF LOGICAL ALGEBRA

Abstract

Significant variables of Boolean functions are found in the article with the help of linear programming. Boolean functions are checked for monotonicity and linearity.

The problem of the shortest covering of a Boolean matrix is generalized, as is the problem of the shortest covering of a Boolean matrix with a given defect. Generalized problem of the shortest covering is reduced to the problem of linear programming. As a consequence we obtain a linear programming problem, to which the classical problem of the shortest covering of a Boolean matrix is reduced.

Examples are given where problems of the theory of Boolean functions are solved with the help of linear programming.

Keywords: optimization, Boolean function, monotonicity, linearity, shortest covering.

Введение

Статья посвящена сведению ряда задач теории булевых функций [1], [2], [9], [10], включая задачу о кратчайшем покрытии булевой матрицы и ее обобщения, к задачам линейного программирования [3, 4] и решению их методами линейного программирования. Такой подход является достаточно эффективным, так как методы решения задач линейного программирования поддерживаются, вообще говоря, во всех современных информационных математических приложениях, включая [5], [6], [7], [8].

Во всех примерах данного исследования применялась надстройка «Поиск решения» (в оригинале «Solver») программного комплекса Excel.

1. Существенные переменные булевых функций

Переменная  называется [2] существенной переменной булевой функции , если найдутся такие значения остальных переменных, при которых выполняется:

                                     (1)

В противном случае, она называется несущественной или фиктивной переменной.

Следовательно, если в таблице истинности функции  существует пара строк, которые различаются только по значениям i-х элементов и по (n+1)-х элементов, то переменная  является существенной, иначе она является фиктивной.

Пусть индексы принимают значения  – элементы таблицы истинности функции  – двоичные (булевы) переменные. Тогда справедлива следующая теорема.

Теорема 1. Проверка переменной  функции  на существенность сводится к задаче линейного программирования, в которой   тогда и только тогда, когда переменная  является существенной:

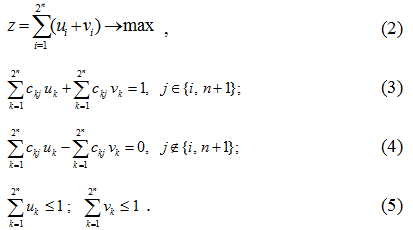
Доказательство. В силу (2, 5) выполняется . Если , то в силу (5) только одна из переменных  принимает значение 1 и только одна из переменных  принимает значение 1, причем в силу (3) индексы этих переменных различны, но тогда из (3, 4) следует (1). В случаях, отличных от , методом «от противного» легко доказывается, что условие (1) не выполняется.

Пример 1. Проверить, что переменная   является фиктивной переменной функции  .

1. В диапазон A1:D8 вводим таблицу истинности.
2. Диапазон Е1:Е8 оставляем за переменными .
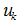3. Диапазон F1:F8 оставляем за переменными .
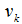4. Для наглядности заливаем диапазон Е1:F8 желтым цветом.
5. В ячейку А9 вводим формулу =СУММПРОИЗВ(A1:A8;$E$1:$E$8) и копируем ее в остальные ячейки диапазона A9:D9.
6. В ячейку А10 вводим формулу =СУММПРОИЗВ(A1:A8;$F$1:$F$8) и копируем ее в остальные ячейки диапазона A10:D10.
7. В ячейку Е9 вводим формулу =СУММ(E1:E8) и копируем ее в F9.
8. В ячейке G10 записываем формулу целевой функции =E9+F9.
9. В ячейку А11 вводим формулу =А9+А10 и копируем ее в D11.
10. В ячейку В11 вводим формулу =В9-В10 и копируем ее в С11.
11. Вызываем надстройку «Поиск решения» и задаем значения параметров (рис. 1).

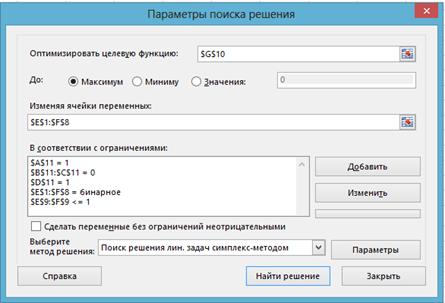
Рис. 1 – Значения параметров проверки х₁ на существенность

12. Кнопка «Найти решение» возвращает сообщение, что решение найдено, и результаты (рис. 2).

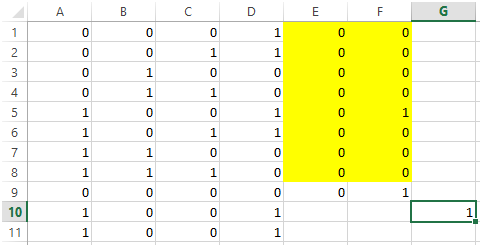
Рис. 2 – Результаты проверки х₁ на существенность

Так как , то переменная  является фиктивной.

2. Монотонность и линейность булевых функций

Функция  называется монотонной [9], если для любых наборов  и  таких, что  такие наборы называются сравнимыми, выполняется:

В противном случае, она немонотонная.

По аналогии с теоремой 1 доказывается следующая теорема.

Теорема 2. Проверка функции  на монотонность сводится к задаче линейного программирования, в которой  тогда и только тогда, когда функция  не монотонная:

 

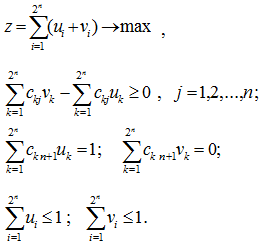
Пример 2. Проверить функцию  на монотонность.

Первые 8 пунктов такие же, как примере 1.

9. В ячейке А11 записываем формулу =А10-А9 и копируем ее в ячейки В11:С11.
10. Вызываем надстройку «Поиск решения» и задаем значения параметров поиска решения (рис. 3).

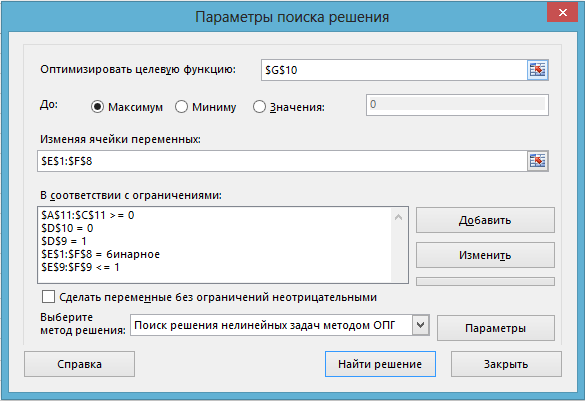
Рис. 3 – Значения параметров проверки на монотонность

12. Кнопка «Найти решение» возвращает сообщение, что решение найдено, и результаты (рис. 4).

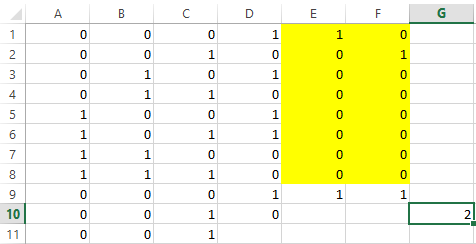
Рис. 4 – Результаты проверки на монотонность

Так как , то функция не монотонная, монотонность, как минимум, нарушается в 1-ой и 2-ой строках таблицы истинности.

Функция  называется линейной [2], если ее можно представить в виде:

Теорема 3. Проверка функции  на линейность сводится к задаче линейного программирования с двоичными переменными  и целочисленными переменными  , которая имеет решение тогда и только тогда, когда функция  линейная:

Пример 3.  Проверить на линейность функцию .

1. Вводим в диапазон A1:D8 таблицу истинности функции.
2. Диапазон A9:D9 оставляем за переменными 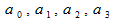(заливаем диапазон желтым цветом), диапазон Е1:Е8 оставляем за переменными 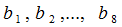(тоже заливаем диапазон желтым цветом).
3. В ячейку G1 вводим формулу =$A$9+СУММПРОИЗВ(A1:C1;$B$9:$D$9) и копируем ее в ячейки G2:G8.
4. В ячейку I1 вводим формулу =G1-2*E1 и копируем ее в ячейки I2:I8.
5. В ячейку Е10 вводим формулу целевой функции =СУММ(A9:D9).
6. Вызываем надстройку «Поиск решения» и задаем значения параметров поиска решения (рис. 5).

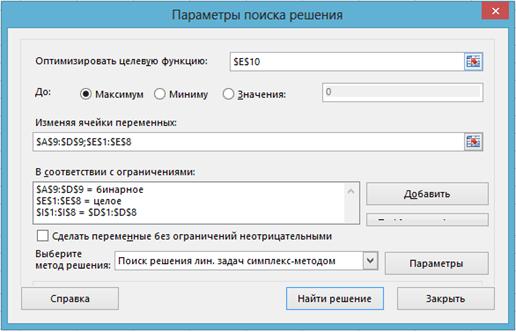
Рис. 5 – Значения параметров проверки на линейность

6. Кнопка «Найти решение» возвращает сообщение, что решение найдено, и результаты (рис. 6).

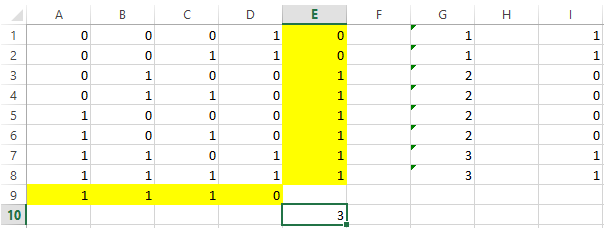
Рис. 6 – Результаты проверки на линейность

Так как решение найдено, то функция является линейной, причем из данных диапазона A9:D9 следует .

3. Кратчайшие покрытия булевых матриц

Пусть задана булева матрица вида  в каждой строке и в каждом столбце которой есть хотя бы одна единица. Строка i называется покрывающей столбец j, если . Под покрытием матрицы С понимают совокупность строк, покрывающих все столбцы матрицы С. Задача о кратчайшем покрытии булевой матрицы С состоит в нахождении покрытия, которое имеет минимальное число строк, такое покрытие называют кратчайшим [9].

Назовем задачу нахождения минимальной совокупности строк матрицы С, покрывающих не менее n-k столбцов, , задачей о кратчайшем покрытии с дефектом k. Понятно, что задача о кратчайшем покрытии является задачей о кратчайшем покрытии с дефектом k =0.

Пусть надо найти решение задачи о кратчайшем покрытии с дефектом k. Введем в рассмотрение булевы переменные , значения которых определим условиями:  = 1, если i-я строка входит в кратчайшее покрытие, иначе  = 0. Дополнительно к этим переменным  введем булевых переменные , значения которых: , если j-й столбец покрывается кратчайшим покрытием с дефектом k, иначе . В этих переменных справедлива следующая теорема.

Теорема 4. Задача о кратчайшем покрытии с дефектом k булевой матрицы С сводится к задаче линейного программирования:

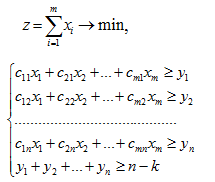
Следствие. Задача о кратчайшем покрытии булевой матрицы С сводится к задаче линейного программирования:

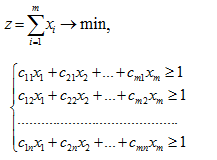
Пример 4.  Найти кратчайшее покрытие булевой матрицы

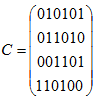
1. Вводим элементы матрицы в диапазон A1:F4, диапазон H1: H4 оставляем за независимыми переменными (заливаем желтым цветом).
2. В ячейку А6 вводим формулу =СУММПРОИЗВ(A1:A4;$H$1:$H$4) и копируем ее в остальные ячейки диапазона A6:F6.
3. Целевую функцию записываем в ячейке I5 формулой =СУММ(H1:H4).
4. Вызываем надстройку «Поиск решения» и задаем значения параметров поиска решения (рис. 7).

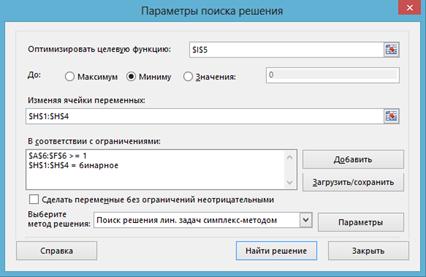
Рис. 7 – Значения параметров нахождения кратчайшего покрытия

5. Команда «Найти решение» возвращает сообщение, что решение найдено, и результаты (рис. 8), показывающие, что кратчайшее покрытие состоит из строк 1, 2, 4.

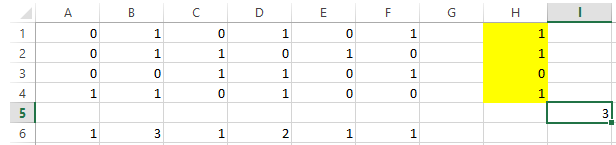
Рис. 8 – Результаты нахождения кратчайшего покрытия

Пример 5.  Найти кратчайшее покрытие с дефектом 1 матрицы С, заданной в примере 4.

Первые 3 пункта такие же как в решении примера 4.

4. Ячейки диапазона A5:F5 оставляем за переменными (заливаем ячейки желтым цветом).
5. В ячейку G5 вводим формулу =СУММ(A5:F5).
6. Вызываем надстройку «Поиск решения» и задаем значения параметров поиска решения (рис. 9).

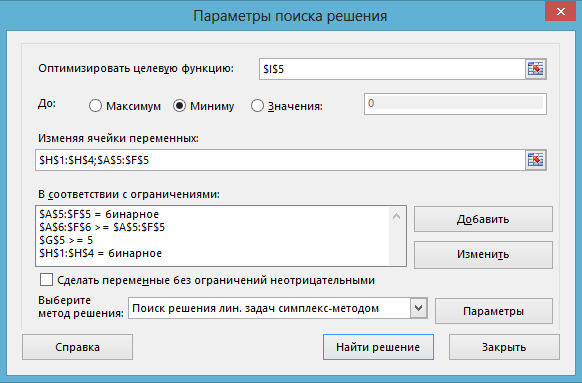
Рис. 9 – Параметры нахождения кратчайшего покрытия с дефектом 1

7. Команда «Найти решение» возвращает сообщение, что решение найдено, и результаты (рис. 10), показывающие, что кратчайшее покрытие дефекта 1 состоит из строк 2, 4:

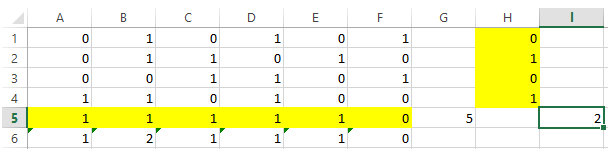
Рис. 10 – Результаты нахождения кратчайшего покрытия с дефектом 1

Заключение

Приведенные примеры показывают, что сведение задач теории булевых функций к задачам линейного программирования позволяет решать их с помощью надстройки «Поиск решения» программного комплекса Excel, а это значительно упрощает решения задач. Поэтому предлагаемые методы решения задач теории булевых функций, основанные на сведении к задачам линейного программирования, несомненно, будут востребованы.

Список литературы / References

1. Ерусалимский Я.М. Дискретная математика: теория, задачи, приложения. 3-е издание. / Я.М. Ерусалимский – М.: Вузовская книга, 2000. – 280 с.
2. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике: Учеб. пособие. / Г.П. Гаврилов, А.А. Сапоженко – 3-е изд., перераб. – М.: ФИЗМАТЛИТ, 2003. – 416 с.
3. Галеев Э.М. Оптимизация: теория, примеры, задачи: Учебное пособие. / Э.М. Галеев – М.: УРСС, 2002. – 304 с.
4. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. / О.П. Кузнецов, Г.М. Адельсон-Вельский – 2-е изд., перераб. и доп. – М.: Энергоатомиздат, 1988. – 480 с.
5. Сдвижков О.А. Дискретная математика и математические методы экономики с применением VBA Excel. / О.А. Сдвижков – М.: ДМК Пресс, 2012. – 212 с.
6. Сдвижков О.А. Математика в Excel 2003. / О.А. Сдвижков – М.: СОЛОН-Пресс, 2005. – 192 с.
7. Сдвижков О.А. Математика на компьютере: Maple 8. / О.А. Сдвижков – М.: СОЛОН-Пресс, 2003. – 176 с.
8. Сдвижков О.А. MathCAD-2000. / О.А. Сдвижков – М.: Издательско-торговая корпорация «Дашков и К», 2002. – 204 с.
9. Супрун В.П. Основы теории булевых функций. / В.П. Супрун – М.: ЛЕНАНД, 2017. – 208 с.
10. Яблонский С.В. Введение в дискретную математику. / С.В. Яблонский – М.: Наука, 1986. – 384 с.

Список литературы на английском языке / References in English

1. Erusalimskij Ja.M. Diskretnaja matematika: teorija, zadachi, prilozhenija. 3-e izdanie [Discrete mathematics: the theory, task, appendix. 3 editions] / Ja.M. Erusalimskij – M.: Vuzovskaja kniga, 2000. – 280 p. [in Russian]
2. Gavrilov G.P., Sapozhenko A.A. Zadachi i uprazhnenija po diskretnoj matematike: Ucheb. posobie. – 3-e izd., pererab. [Tasks and exercises on discrete mathematics: studies] / G.P. Gavrilov, A.A. Sapozhenko – M.: FIZMATLIT, 2003. – 416 p. [in Russian]
3. Galeev Je.M. Optimizacija: teorija, primery, zadachi: Uchebnoe posobie. [Optimization: the theory, examples, tasks] / Je.M. Galeev – M.: URSS, 2002. – 304 p. [in Russian]
4. Kuznecov O.P., Adel'son-Vel'skij G.M. Diskretnaja matematika dlja inzhenera [Discrete mathematics for the engineer] / O.P. Kuznecov, G.M. Adelson-Velskij / – 2-e izd., pererab. i dop. – M.: Jenergoatomizdat, 1988. – 480 p. [in Russian]
5. Sdvizhkov O.A. Diskretnaja matematika i matematicheskie metody jekonomiki s primeneniem VBA Excel [Discrete mathematics and mathematical methods of economy with application VBA Excel] / O.A. Sdvizhkov – M.: DMK Press, 2012. – 212 p. [in Russian]
6. Sdvizhkov O.A. Matematika v Excel 2003 [Mathematics in Excel 2003] / O.A. Sdvizhkov – M.: SOLON-Press, 2005. – 192 p. [in Russian]
7. Sdvizhkov O.A. Matematika na komp'jutere: Maple 8 [Mathematics on the computer: Maple 8] / O.A. Sdvizhkov – M.: SOLON-Press, 2003. – 176 p. [in Russian]
8. Sdvizhkov O.A. MathCAD-2000 [MathCAD-2000] / O.A. Sdvizhkov – M.: Izdatelsko-torgovaja korporacija «Dashkov and C», 2002. – 204 p. [in Russian]
9. Suprun V.P. Osnovy teorii bulevyh funkcij [Bases of the theory Boolean functions] / V.P. Suprun – M.: LENAND, 2017. – 208 p. [in Russian]
10. Jablonskij S.V. Vvedenie v diskretnuju matematiku [Introduction in discrete mathematics] / S.V. Jablonskij – M.: Science, 1986. – 384 p. [in Russian]