ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ВИХРЕВОЙ ТРУБЫ

Кукис В.С.¹, Шабалин Д.В.², Омельченко Е.А.³

¹ORSID: 000-0002-8234-2009, Профессор, Доктор технических наук, профессор, Уральский государственный университет (национальный исследовательский университет), ²Военный учебно-научный центр Сухопутных войск «Общевойсковая академия Вооруженных Сил Российской Федерации», ³Кандидат технических наук, Омский автобронетанковый инженерный институт

ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ВИХРЕВОЙ ТРУБЫ

Аннотация

В статье рассмотрена методика решения аналитической задачи оптимизации вихревой трубы. Авторским коллективом предложен способ графического представления функции от нескольких переменных, позволяющий с помощью простых геометрических операций исследовать функциональные зависимости. Преимущество предлагаемого номографического способа перед расчетным состоит в простоте использования. Он позволяет с достаточной для большинства инженерных расчетов точностью, по расположению оптимальной области в факторном пространстве, производить предварительные исследования рациональных геометрических параметров вихревой трубы.

Ключевые слова: вихревая туба, температура, давление, геометрические параметры.

Kukis V. S.¹, Shabalin D. B.². Omelchenko E.A.³

¹ORSID: 000-0002-8234-2009, Professor, PhD in Engineering, Federal state budgetary educational institution of higher professional education "South Ural state University" (national research University), ²PhD in Engineering, Military educational scientific center of Land forces «Combined arms Academy of the Armed Forces of the Russian Federation», ³PhD in Engineering, Omsk tank-automotive engineering Institute

 PARAMETER OPTIMIZATION OF VORTEX TUBE

Abstract

The article describes the method of analytic solutions of the optimization problem of the vortex tube. A group of authors proposed a method of graphic representation of functions of several variables, allowing to explore the functional dependencies using simple geometrical operations. The advantage of the proposed method over nomogrammic calculation is ease of use. He makes enough for most engineering calculations accuracy on the location of the optimal domain in the factor space, to make preliminary studies of rational geometric parameters of the vortex tube.

Keywords: vortex tube, temperature, pressure, geometric parameters.

Газотурбинный наддув, как средство повышения мощности и экономичности силовых установок автомобильного транспорта при всех имеющихся преимуществах имеет и ряд недостатков. Прежде всего, это широкий диапазон изменения температуры свежего заряда воздуха, связанный как с режимом работы двигателя, так и с параметрами окружающей среды. Современные исследователи сходятся во мнении о необходимости стабилизации температуры свежего заряда воздуха на определенном уровне [1]. Широко применяемое в настоящее время охлаждение наддувочного воздуха, которое было предложено еще Рудольфом Дизелем, не является достаточно эффективным решением проблемы обеспечения стабильности показателей температурных параметров систем воздухоснабжения современных силовых установок мобильных машин.

Для решения задачи регулирования температуры наддувочного воздуха авторами предлагается использовать вихревой эффект (эффект Ранка-Хилша) – эффект разделения газа или жидкости в закрученном потоке. Устройства на основе вихревого эффекта – вихревые трубы – позволяют получать как охлажденный, так и нагретый воздух на основе одного и того же физического эффекта [2].

На рис. 1 показана возможная схема системы, позволяющей обеспечивать дифференцированное регулирование, вплоть до полной стабилизации температуры, наддувочного воздуха с использованием вихревой трубы [3].

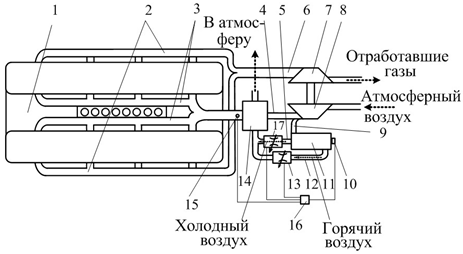
Рис. 1 –  Схема системы стабилизации температуры наддувочного воздуха при работе двигателя на различных режимах с использованием вихревой трубы: 1 – поршневой ДВС; 2 – выпускные коллекторы; 3 – впускные коллекторы; 4 – трубопровод; 5 – трубопровод холодного воздуха; 6 – выхлопная труба; 7 – газовая турбина; 8 – компрессор; 9 – патрубок; 10 – дроссельный вентиль; 11 – вихревая труба; 12 – трубопровод теплого воздуха; 13 – клапан регулирования количества теплого воздуха; 14 – воздухо-воздушный охладитель наддувочного воздуха; 15 – датчик температуры; 16 – блок регулирования; 17 клапан регулирования количества холодного воздуха

В качестве источника охлажденного воздуха можно использовать как отдельную вихревую трубу, так и модуль, состоящий из нескольких вихревых труб.

Преимущества вихревых труб заключаются в высокой температурной эффективности (однако при сравнительно низком общем КПД), надежности, простоте изготовления, малой стоимости, устойчивости к высокоэнергетическим внешним воздействиям. Эти качества вихревых труб, а так же возможность их применения в силовых установках любой мощности, вызывают определенный интерес у производителей мобильных машин военного и двойного назначения.

Вихревой эффект является чрезвычайно сложным объектом для моделирования. До появления высокопроизводительной вычислительной техники аналитические методы (в частности, механики сплошной среды) не давали возможности достаточно адекватно представить вихревой эффект. Поэтому ранее проектирование вихревых труб вели на основе эмпирических правил и закономерностей.

В работе [4] была рассмотрена физико-математическая модель вихревых труб, предназначенных для регулирования температуры наддувочного воздуха. В зависимости от задания входных характеристик потока эта модель может быть использована для определения оптимальных геометрических параметров вихревой трубы, а также давления на входе в нее и для любых газовых потоков.

Для моделирования вихревой трубы в данной работе используется метод динамики частиц, в полной мере использующий возможности современной вычислительной техники. Этот метод позволяет с высокой степенью адекватности перенести в модель физические свойства воздушной среды, с высокой степенью детализации представить геометрию вихревой трубы, а также получить исчерпывающую информацию о распределениях температуры и скорости в рабочей области устройства.

На рис. 2 представлены результаты моделирования параметров газа в вихревой трубе, полученные методом динамики частиц.

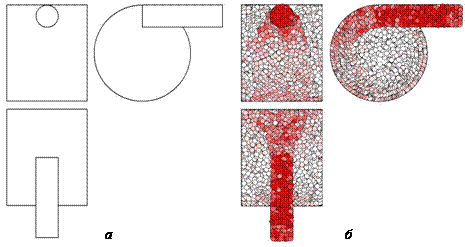
Рис 2 – Вихревая труба в модели (три проекции): представление фрагмента вихревой трубы в модели в виде двух цилиндров (а); результат моделирования – движение элементов воздуха в вихревой трубе (б), уровень красного цвета элемента пропорционален давлению воздуха

 

В настоящей статье модель и программа [5] использованы для определения оптимальных геометрических параметров вихревой трубы, а также давления воздуха на входе в нее.

Аналитически задачу оптимизации можно записать следующим образом:

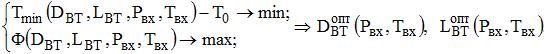  (1)

где T_min – минимальная температура воздуха; D_ВТ – диаметр вихревой трубы; L_ВТ – длина вихревой трубы; P_вх – давление воздуха на входе в вихревую трубу; T_вх – температура воздуха на входе в вихревой трубе; T – температура окружающего воздуха;  – оптимальный диаметр вихревой трубы;  – оптимальная длина вихревой трубы; Ф – холодопроизводительность.

На рис. 3 показана картограмма распределения температуры в вихревой трубе с различными геометрическими параметрами L_ВТ и D_ВТ.

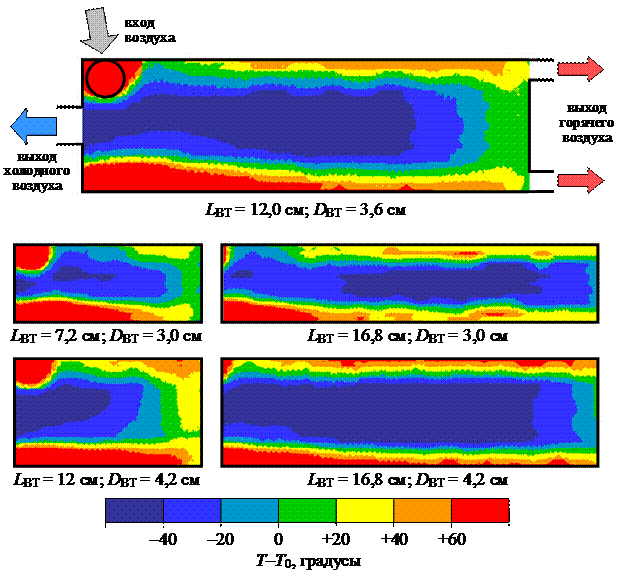
Рис. 3 – Картограмма распределения температуры в вихревых трубах с различными геометрическими параметрами L_ВТ и D_ВТ

 

Для получения аналитического вида функций [T_min(D_ВТ, L_ВТ)–T₀] и Ф(D_ВТ, L_ВТ) произведена их аппроксимация полиномами второго порядка следующего вида:

K(D_ВТ, L_ВТ) = a₁ D_ВТ² + a₂ L_ВТ² + a₃ D_ВТ∙L_ВТ + a₄ D_ВТ + a₅ L_ВТ + a₆,      (2)

где K – критерий оптимизации (T_min–T₀) или Ф; a₁ ... a₆ – коэффициенты полинома.

Коэффициенты полиномов определены методом наименьших квадратов (МНК) [6, 7], который заключался в минимизации суммы квадратов отклонений аналитической зависимости от результатов расчетов:

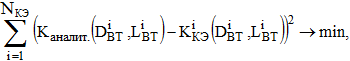 (3)

где i и N_КЭ – порядковый номер и общее количество компьютерных экспериментов; K_аналит – искомая аналитическая (полиномиальная) зависимость критерия K от факторов;  – значения критерия K, определенные в i-м расчете с параметрами D_ВТ и L_ВТ.

Аппроксимация методом МНК реализована с помощью математической программы MathCAD 14 [8]. В результате для критериев получены следующие аналитические формулы:

T_min(D_ВТ, L_ВТ) – T₀ = 9,72 D_ВТ² + 0,043 L_ВТ² – 1,04 D_ВТ∙L_ВТ – 68,9 D_ВТ + 3,65 L_ВТ + 79,0;  (4) Ф(D_ВТ, L_ВТ) = – 0,556 D_ВТ² – 1,09·10^–3 L_ВТ² + 8,69·10^–3 D_ВТ∙L_ВТ + 4,70 D_ВТ + 0,021 L_ВТ – 8,59,(5) где (T_min – T₀) измеряется в градусах, Ф – в кВт.

Полученные формулы могут использоваться для быстрой оценки (без выполнения реальных или компьютерных экспериментов) показателей эффективности вихревой трубы.

На рис. 4 показано влияние геометрических параметров вихревой трубы на показатели ее эффективности (T_min–T₀) и Ф, а на рис. 5 – номограммы для оптимизации геометрических параметров вихревой трубы (затемнены благоприятные области факторного пространства).

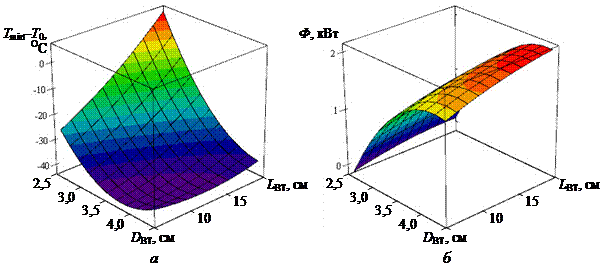
Рис. 4 – Графики влияния диаметра и длины вихревой трубы на показатели ее эффективности

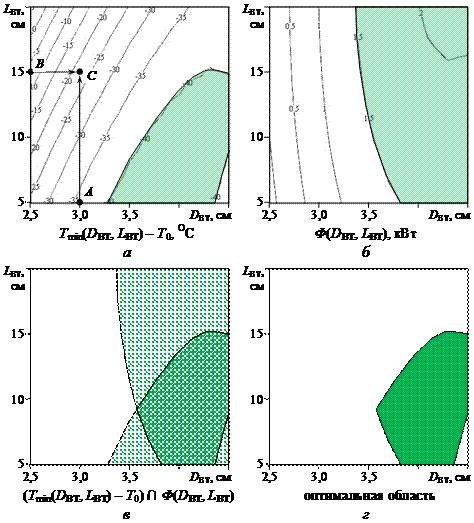
Рис. 5 – Номограммы для оптимизации геометрических параметров вихревой трубы D_ВТ и L_ВТ

Преимущество предлагаемого номографического способа перед расчетным состоит в простоте использования. Он позволяет с достаточной для большинства инженерных расчетов точностью, по расположению оптимальной области в факторном пространстве, производить предварительные исследования рациональных геометрических параметров вихревой трубы.

Оптимальные геометрические параметры вихревой трубы, определенные по предлагаемым номограммам, следующие: диаметр вихревой трубы от 3,7 до 4,5 см; длина вихревой трубы от 5 до 14 см. При таких параметрах вихревая труба обеспечивает охлаждение поступающего воздуха более чем на 40 ^°С, и имеет холодопроизводительность более 1,5 кВт.

Таким образом, полученные номограммы позволяют без сложных математических вычислений производить предварительные исследования по определению оптимальных геометрических параметров вихревых труб и параметров газа на ее ходе.

Литература

1. Кукис В.С., Берестнев Г.А. Повышение эффективности наддува за счет стабилизации температуры воздуха, поступающего в цилиндры дизеля, работающего на переменных режимах // Тр. Международного Форума по проблемам науки, техники и образования. – М.: Академия наук о земле, 2005. – С. 111–113.
2. Меркулов А.П. Вихревой эффект и его применение в технике. – Самара: Оптима, 1997. – 184 с.
3. Кукис В.С., Романов В.А., Шабалин Д.В. Использование вихревых труб в поршневых двигателях внутреннего сгорания. – СПб.: Изд-во ВА МТО. 2015. – 215 с.
4. Кукис В.С., Шабалин Д.В. Физико-математическая модель вихревых труб для регулирования температуры наддувочного воздуха // Научные проблемы транспорта Сибири и Дальнего Востока. – 2015. №1. – С. 129‑133.
5. Шабалин Д.В., Кукис В.С., Посметьев В.В. Программа моделирования вихревого охладителя наддувочного воздуха (Свидетельство о государственной регистрации программы для ЭВМ) № 2015618150. Выдано 31.07.2015.
6. Линник Ю.В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. – М.: ФИЗМАТЛИТ, 1958. ‑ 336 с.
7. Лоусон Ч. Численное решение задач метода наименьших квадратов. – М.:Наука, 1986. ‑ 232 с.
8. Тарасевич Ю. Ю. Численные методы на Mathcad’е: учебное пособие – Астрахань: Изд-во АГУ, 2000. – 70 с.

Reference

1. Kukis V.S., Berestnev G.A. Povyshenie jeffektivnosti nadduva za schet stabilizacii temperatury vozduha, postupajushhego v cilindry dizelja, rabotajushhego na peremennyh rezhimah // Tr. Mezhdunarodnogo Foruma po problemam nauki, tehniki i obrazovanija. – M.: Akademija nauk o zemle, 2005. – S. 111–113. [in Russian]
2. Merkulov A.P. Vihrevoj jeffekt i ego primenenie v tehnike. – Samara: Optima, 1997. – 184 s. [in Russian]
3. Kukis V.S., Romanov V.A., Shabalin D.V. Ispol'zovanie vihrevyh trub v porshnevyh dvigateljah vnutrennego sgoranija. – SPb.: Izd-vo VA MTO. 2015. – 215 s. [in Russian]
4. Kukis V.S., Shabalin D.V. Fiziko-matematicheskaja model' vihrevyh trub dlja regulirovanija temperatury nadduvochnogo vozduha // Nauchnye problemy transporta Sibiri i Dal'nego Vostoka. – 2015. №1. – S. 129–133. [in Russian]
5. Shabalin D.V., Kukis V.S., Posmet'ev V.V. Programma modelirovanija vihrevogo ohladitelja nadduvochnogo vozduha (Svidetel'stvo o gosudarstvennoj registracii programmy dlja JeVM) № 2015618150. Vydano 31.07.2015. [in Russian]
6. Linnik Ju.V. Metod naimen'shih kvadratov i osnovy matematiko-statisticheskoj teorii obrabotki nabljudenij. – M.: FIZMATLIT, 1958. – 336 s. [in Russian]
7. Louson Ch. Chislennoe reshenie zadach metoda naimen'shih kvadratov. – M.:Nauka, 1986. – 232 s. [in Russian]
8. Tarasevich Ju. Ju. Chislennye metody na Mathcad’e: uchebnoe posobie – Astrahan': Izd-vo AGU, 2000. – 70 s. [in Russian]