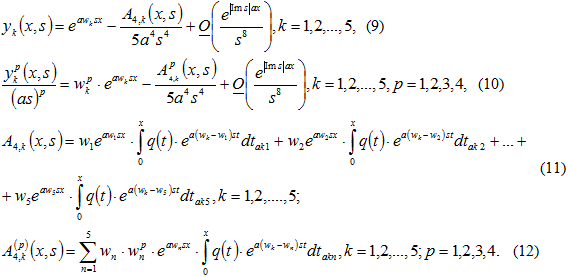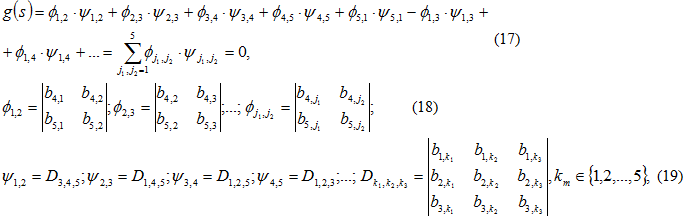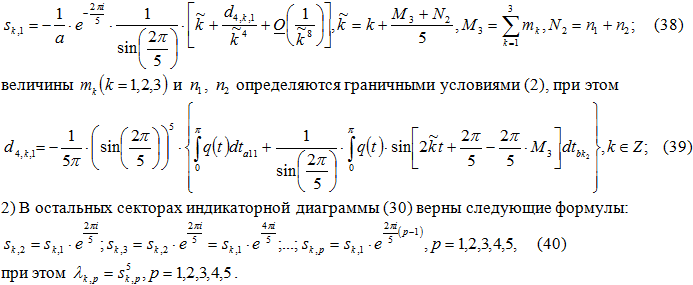ОБ АСИМПТОТИКЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ МОДЕЛЬНОЙ КРАЕВОЙ ЗАДАЧИ ДЛЯ СЕМЕЙСТВА ДИФФЕРЕНЦИАЛЬНЫХ ОПЕРАТОРОВ С СУММИРУЕМЫМ ПОТЕНЦИАЛОМ
Митрохин С. И.
Кандидат физико-математических наук, доцент, профессор РАЕ, научно-исследовательский вычислительный центр МГУ им. М. В. Ломоносова
ОБ АСИМПТОТИКЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ МОДЕЛЬНОЙ КРАЕВОЙ ЗАДАЧИ ДЛЯ СЕМЕЙСТВА ДИФФЕРЕНЦИАЛЬНЫХ ОПЕРАТОРОВ С СУММИРУЕМЫМ ПОТЕНЦИАЛОМ
Аннотация
Рассматривается модельная краевая задача для семейства дифференциальных операторов с разделёнными граничными условиями с суммируемым потенциалом. Уравнение, задающее оператор, сведено к интегральному уравнению. Методом последовательных приближений выведена асимптотика решений соответствующего дифференциального уравнения при больших значениях спектрального параметра. Получено уравнение на собственные значения изучаемого оператора. Изучена индикаторная диаграмма полученного уравнения. Исследована асимптотика собственных значений изучаемого семейства дифференциальных операторов.
Ключевые слова: краевая задача, дифференциальный оператор, спектральный параметр, суммируемый потенциал, асимптотика собственных значений.
Mitrokhin S. I.
PhD in Physics and Mathematics, associate professor, professor RAE, Scientific Research Computer Center of Moscow State University
ABOUT ASYMPTOTICS OF THE EIGENVALUES OF MODEL BOUNDARY PROBLEM FOR THE FAMILY OF DIFFERENTIAL OPERATORS WITH SUMMABLE POTENTIAL
Abstract
The model boundary value problem for a family of differential operators with separated boundary conditions with a summable potential is studied. The asymptotic of solutions of the corresponding differential equations for large values of the spectral parameter is deduced. The equation for the eigenvalues of the studied operators is obtained. The asymptotics of the eigenvalues of the studied family of differential operators is analyzed.
Keywords: boundary value problem, differential operator, spectral parameter, summable potential, asymptotics of the eigenvalues.
Введение. Постановка задачи. Исторический обзор.
Исследуем модельную краевую задачу для дифференциального оператора пятого порядка, определяемого дифференциальным уравнением
В дифференциальном уравнении (1) число ![]() - спектральный параметр, функция
- спектральный параметр, функция ![]() - весовая функция, функция
- весовая функция, функция ![]() - потенциал, который является суммируемой функцией на отрезке
- потенциал, который является суммируемой функцией на отрезке ![]() :
:
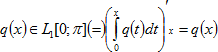 (3)
почти всюду на отрезке
(3)
почти всюду на отрезке Все колебательные процессы физики и механики (колебания волн, стержней, мостов, балок, земной почвы) описываются дифференциальные уравнениями типа (1) с граничными условиями, аналогичными условиям (2). Дифференциальные операторы нечётного порядка вида (1)-(2) раньше фактически не изучались. Операторы чётного порядка раньше изучались при условии достаточно гладких потенциалов ![]() . В работах [1] и [2] исследованы операторы при условии бесконечно гладкого потенциала.
. В работах [1] и [2] исследованы операторы при условии бесконечно гладкого потенциала.
Случаи кусочно-гладкой весовой функции, разрывной весовой функции, разрывных коэффициентов изучены в работах [3], [4], [5]. В работе [6] впервые изучены операторы Штурма-Лиувилля с суммируемым потенциалом и найдена асимптотика любого порядка собственных значений и собственных функций. В работе [7] автором получена асимптотика собственных значений дифференциального оператора четвёртого порядка с суммируемыми коэффициентами. В работе [8] исследованы спектральные свойства дифференциального оператора шестого порядка с суммирующими коэффициентами с запаздывающим аргументом. Рассматривая граничные условия (2), мы одновременно исследуем целое семейство дифференциальных операторов и ищем асимптотику собственных значений таких операторов.
1. Изучение поведения решений дифференциального уравнения (1) при ![]() . Пусть
. Пусть
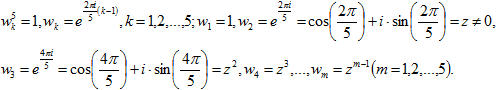 (4)
Для этих чисел справедливы соотношения:
(4)
Для этих чисел справедливы соотношения:
Числа ![]() из (4) – (5) делят единичную окружность на пять равных частей, числа
из (4) – (5) делят единичную окружность на пять равных частей, числа ![]() и являются комплексно-сопряженными:
и являются комплексно-сопряженными:
![]() (6)
(6)
Для дальнейших выкладок мы введём полезное обозначение ![]()
Дифференциальное уравнение (1) можно свести к интегральному уравнению с помощью методов, продемонстрированных в работах [9, гл. 2], [10, гл. 1], [7], [8].
Теорема 1. Пусть - решение дифференциального уравнения (1). Оно удовлетворяет интегральному уравнению Вольтерры следующего вида:
![]() (7)
(7)
Формула (7) выводится методом вариации постоянных с применением свойств (5).
Для нахождения асимптотики решений дифференциального уравнения (1) (при больших значениях спектрального параметра λ) применим интегральное уравнение (7) и метод последовательных приближений Пикара. Находим y(t,s) из уравнения (7), подставим это выражение в уравнение (7), сделаем необходимые преобразования. В результате докажем следующее утверждение.
Теорема 2. Обозначим через ![]() общее решение дифференциального уравнения (1). Общий вид функции
общее решение дифференциального уравнения (1). Общий вид функции ![]() представляется следующим образом:
представляется следующим образом:
![]() (8)
(8)
![]() - произвольные постоянные,
- произвольные постоянные,
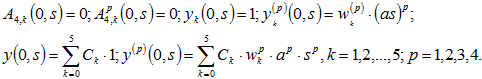 (13)
(13)
Оценки (9) – (12) мы получили аналогично оценкам, выведенным для гладкого потенциала ![]() в монографиях [10, глава 2], [11, глава 1].
в монографиях [10, глава 2], [11, глава 1].
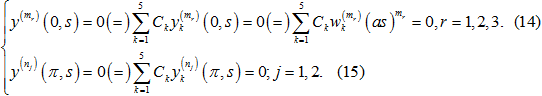
Когда система (14) – (15) (из пяти уравнений с пятью неизвестными ![]() ) будет иметь ненулевые решения (
) будет иметь ненулевые решения (![]() )? Это происходит только в том случае, когда определитель этой системы будет равен нулю. Поэтому верно следующее утверждение.
)? Это происходит только в том случае, когда определитель этой системы будет равен нулю. Поэтому верно следующее утверждение.
Теорема 3. Собственные значения дифференциального оператора (1) – (2) – (3) являются корнями уравнения, которое имеет следующий вид:
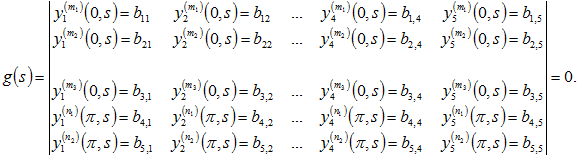 (16)
(16)
В определителе ![]() из (16) применим начальные условия (13) и поделим в k-ой строке на
из (16) применим начальные условия (13) и поделим в k-ой строке на ![]() . Применим теорему Лапласа о разложении определителя
. Применим теорему Лапласа о разложении определителя ![]() по последним двум строчкам для изучения корней уравнения (16). В результате находим:
по последним двум строчкам для изучения корней уравнения (16). В результате находим:
при этом ![]() - элементы определителя
- элементы определителя ![]() из (16).
из (16).
Знаки «+» и «-» элементов суммы (17) находятся по известным правилам: они зависят от чётности или нечётности перестановок, которые образуют индексы элементов ![]() .
.
Вычислим в явном виде некоторые из определителей ![]() из (19), которые понадобятся нам в процессе исследования спектра краевой задачи (1) – (2) – (3), используя очень удобные обозначения (4) – (6).
из (19), которые понадобятся нам в процессе исследования спектра краевой задачи (1) – (2) – (3), используя очень удобные обозначения (4) – (6).
Из формул (19), (13), (16) находим:
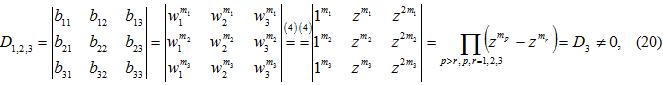
(определитель ![]() - это определитель Вандермонда чисел
- это определитель Вандермонда чисел ![]() ).
).
Применяя свойства определителей и формулы (4) – (6), выводим:
3. Вычисление асимптотики собственных значений дифференциального оператора(1)-(2)-(3). Для изучения уравнения (16) на собственные значения, которое мы привели к виду (17) – (19), подставим в него формулы (23) – (28) и (20) – (22) и видим, что основное приближение получившегося уравнения записывается следующей формулой:
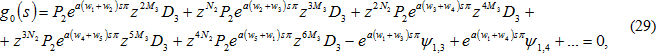
формулы для ![]() мы не приводим, в дальнейшем они нам не понадобятся.
мы не приводим, в дальнейшем они нам не понадобятся.
Чтобы вывести асимптотику корней уравнения (29) (а также уравнений (16), (17) – (19)) необходимо изучить так называемую индикаторную диаграмму этого уравнения (см. [13, глава 12]), т.е. выпуклую оболочку множества показателей экспонент, входящих в уравнение (29). Следовательно, нам необходимо исследовать выпуклую оболочку множества точек ![]() . Из правила сложения векторов, применяя формулы (4)-(6), из геометрических соображений следует, что
. Из правила сложения векторов, применяя формулы (4)-(6), из геометрических соображений следует, что ![]() , и т.д. Значит, выпуклой оболочкой множества точек является правильный пятиугольник
, и т.д. Значит, выпуклой оболочкой множества точек является правильный пятиугольник ![]() , его вершинами являются точки
, его вершинами являются точки ![]() . Поэтому индикаторная диаграмма уравнения (29) имеет следующий вид:
. Поэтому индикаторная диаграмма уравнения (29) имеет следующий вид:
![]()
Из общей теории (см. [11, глава 12], [12]) нахождения корней уравнений (29), (16), (17) – (19) следует, что корни этих уравнений лежат в пяти секторах, определяемых пятиугольником ![]() из (30), бесконечно малого раствора, биссектрисы которых перпендикулярны сторонам этого пятиугольника.
из (30), бесконечно малого раствора, биссектрисы которых перпендикулярны сторонам этого пятиугольника.
Вычислим асимптотику корней уравнения (17) – (19) в секторе , биссектриса которого перпендикулярна отрезку ![]() . В этом секторе на асимптотику корней влияют только экспоненты с показателями
. В этом секторе на асимптотику корней влияют только экспоненты с показателями ![]() , остальные экспоненты в этом секторе представляют собой бесконечно малые величины. Справедливо следующее утверждение.
, остальные экспоненты в этом секторе представляют собой бесконечно малые величины. Справедливо следующее утверждение.
Теорема 4. В секторе 1) индикаторной диаграммы (30), биссектриса которого перпендикулярна отрезку ![]() , собственные значения дифференциального оператора (1) – (2) – (3) являются корнями уравнения, которое имеет следующий вид:
, собственные значения дифференциального оператора (1) – (2) – (3) являются корнями уравнения, которое имеет следующий вид:
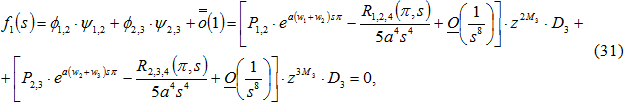
где ![]() , функции
, функции ![]() определены формулами (24), (26).
определены формулами (24), (26).
Используя асимптотические формулы (11) – (12), разложим получившийся определитель по столбцам на сумму определителей, сделаем необходимые выкладки, аналогичные работам [12]. [7] и [8], придём к выводу о справедливости следующего утверждения.
Теорема 5. Собственные значения дифференциального оператора (1) – (2) – (3) в секторе 1) индикаторной диаграммы подчиняются асимптотике, которая вычисляется по следующей формуле:
![]()
Чтобы доказать теорему 5, необходимо доказать, что коэффициенты ![]() из (32) находятся единственным образом, причём в явном виде.
из (32) находятся единственным образом, причём в явном виде.
Используя формулы Тейлора, выводим:
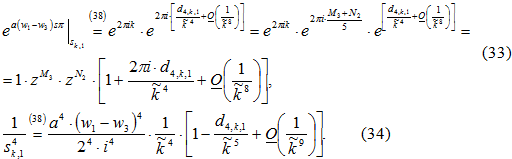
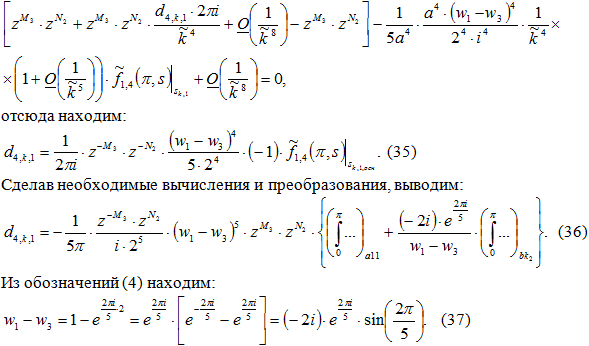
Применяя формулы (33)-(37), сформулируем теорему 5 следующим образом.
Теорема 6. 1) Асимптотика собственных значений оператора (1) – (2) – (3) в секторе 1) ![]() индикаторной диаграммы (30) находится по следующей формуле:
индикаторной диаграммы (30) находится по следующей формуле:
Доказательство формул (40) осуществляется аналогично выводу формул (31)-(39) для сектора 1). Формулы (38) – (40) позволяют вычислить асимптотику собственных функций дифференциального оператора (1) – (2) – (3).
Литература
- Лидский В. Б., Садовничий В. А. Асимптотические формулы для корней одного класса целых функций // Математический сборник. 1968. Т. 65, № 4. С. 558-566.
- Садовничий В. А. О следах обыкновенных дифференциальных операторов высших порядков // Математический сборник. 1967. Т. 72, № 2. С. 293-310.
- Ильин В. А. О сходимости разложений по собственным функциям в точках разрыва коэффициентов дифференциального оператора // Математические заметки. 1977. Т. 22, № 5. С. 698-723.
- Митрохин С. И. О некоторых спектральных свойствах дифференциальных операторов второго порядка с разрывной весовой функцией // Доклады РАН. 1997. Т. 356, № 1. С. 13-15.
- Митрохин С. И. О формулах регуляризованных следов для дифференциальных операторов второго порядка с разрывными коэффициентами // Вестник МГУ. Сер.: матем., мех. 1986. № 6. С. 3-6.
- Винокуров В. А., Садовничий В. А. Асимптотика любого порядка собственных значений и собственных функций краевой задачи Штурма—Лиувилля на отрезке с суммируемым потенциалом // Известия РАН. Сер.: матем. 2000. Т. 64, № 4. С. 47-108.
- Митрохин С. И. Асимптотика собственных значений дифференциального оператора четвёртого порядка с суммируемыми коэффициентами // Вестник Московского университета. Сер.: матем., мех. 2009. № 3. С. 14-17.
- Митрохин С. И. О спектральных свойствах одного дифференциального оператора с суммирующими коэффициентами с запаздывающим аргументом // Уфимский математический журнал. 2011. Т. 3, №4. С. 95-115.
- Наймарк М. А. Линейные дифференциальные операторы. М.: Наука, 1969. 528с.
- Юрко В. А. Введение в теорию обратных спектральных задач. М.: Физматлит, 2007. 384с.
- Беллман Р., Кук К. Л. Дифференциально-разностные уравнения. М.: Мир, 1967. 548 с.
- Садовничий В. А., Любишкин В. А. О некоторых новых результатах теории регуляризованных следов дифференциальных операторов // Дифференциальные уравнения. 1982. Т. 18, № 1. С. 109-116.
References
- Lidskij V. B., Sadovnichij V. A. Asimptoticheskie formuly dlja kornej odnogo klassa celyh funkcij [Asymptotic formulas for roots of one class of entire functions // Mathematical collection] // Matematicheskij sbornik. 1968. V. 65. Iss. 4. P. 558-566. [in Russian].
- Sadovnichij V. A. O sledah obyknovennyh differencial'nyh operatorov vysshih porjadkov [About traces of ordinary differential operators of the highest orders // Mathematical collection] // Matematicheskij sbornik. V. 72. Iss. 2. P. 293-310. [in Russian].
- Il'in V. A. O shodimosti razlozhenij po sobstvennym funkcijam v tochkah razryva kojefficientov differencial'nogo operatora [About convergence of eigenfunction expansions at points of discontinuity of coefficients of the differential operator // Mathematical notes] // Matematicheskie zametki. 1977. V. 22. Iss. 5. P. 698-723. [in Russian].
- Mitrohin S. I. O nekotoryh spektral'nyh svojstvah differencial'nyh operatorov vtorogo porjadka s razryvnoj vesovoj funkciej [About some spectral properties of differential operators of the second order with discontinuous weight function // Reports of the Russian Academy of Sciences] // Doklady RAN. 1997. 356. Iss. 1. P. 13-15. [in Russian].
- Mitrohin S. I. O formulah reguljarizovannyh sledov dlja differencial'nyh operatorov vtorogo porjadka s razryvnymi kojefficientami [On formulas for regularized traces for differential operators of the second order with discontinuous coefficients // Vestnik MGU. Series: Mathematics, mechanics] // Vestnik MGU. Seriya: matematika, mehanika. 1986. Iss. 6. P. 3-6. [in Russian].
- Vinokurov V. A., Sadovnichij V. A. Asimptotika ljubogo porjadka sobstvennyh znachenij i sobstvennyh funkcij kraevoj zadachi Shturma—Liuvillja na otrezke s summiruemym potencialom [Asymptotics of any order for the eigenvalues and the eigenfunctions of the boundary value Sturm—Liouville problem on a segment with a summable potential // Izvestiya RAN. Series: mathematics] // Izvestija RAN. Ser.: matem. V. 64. Iss. 4. P. 47-108. [in Russian].
- Mitrohin S. I. Asimptotika sobstvennyh znachenij differencial'nogo operatora chetvjortogo porjadka s summiruemymi kojefficientami [Asymptotics of the eigenvalues of a differential operator of the fourth order with integrable coefficients // Bulletin of Moscow University. Series: Mathematics, mechanics] // Vestnik Moskovskogo universiteta. Ser.: matematika, mehanika. 2009. Iss. 3. P. 14-17. [in Russian].
- Mitrohin S. I. O spektral'nyh svojstvah odnogo differencial'nogo operatora s summiruemymi kojefficientami s zapazdyvajushhim argumentom [On spectral properties of one differential operator with summable coefficients with a retarded argument // Ufa mathematical Journal] // Ufimskij matematicheskij zhurnal. 2011. V. 3, Iss. 4. P. 95-115. [in Russian].
- Najmark M. A. Linejnye differencial'nye operatory [Linear differential operators. M.: Nauka]. M.: Nauka, 528 p. [in Russian].
- Jurko V. A. Vvedenie v teoriju obratnyh spektral'nyh zadach [Introduction to the theory of inverse spectral problems. M.: Fizmatlit]. M.: Fizmatlit. 2007. 384 p. [in Russian].
- Bellman R., Kuk K. L. Differencial'no-raznostnye uravnenija [Differential-difference equations. M.: World]. M.: Mir, 1967. 548 p. [in Russian].
- Sadovnichij V. A., Ljubishkin V. A. O nekotoryh novyh rezul'tatah teorii reguljarizovannyh sledov differencial'nyh operatorov [About some new results of the theory of regularized traces of differential operators // Different. equations] // Differencial'nye uravnenija. 1982. V. 18. Iss.1. P. 109-116. [in Russian].