МИНИМИЗАЦИЯ ЧИСЛА ЛОКАЛЬНЫХ ЦЕЛЕЙ СИСТЕМЫ

Двадцатов Р.В.

ORCID 0000-0003-2342-7624, Аспирант, Санкт-Петербургский горный университет

МИНИМИЗАЦИЯ ЧИСЛА ЛОКАЛЬНЫХ ЦЕЛЕЙ СИСТЕМЫ

Аннотация

В данной работе рассматривается методика минимизации локальных целей. Для примера взято производство азотной кислоты. В качестве целей выбрано два направления увеличение надежности производства и снижение стоимости продукции. Составляется древо целей. Для расчетов необходимо знать вес целей, который в этом примере известен заранее. Составляется когнитивная карта, отображающая взаимовлияние локальных целей. Вычисляем степень достижимости локальных целей, по формуле, представленной в статье. Затем делаем минимизацию числа локальных целей по определенному алгоритму.

Ключевые слова: Минимизация локальных целей, многокритериальная оптимизация, экспертная оценка, выбор множества альтернатив.

Dvadcatov R.V.

ORCID 0000-0003-2342-7624, Postgraduate student, Saint - Petersburg Mining University

MINIMIZING THE NUMBER OF LOCAL OBJECTIVES SYSTEM

Abstract

In this paper, the technique of minimizing local purposes. As an example, taken the production of nitric acid. In two directions increase the reliability of production and reducing the cost of production is chosen as targets. Tree component goals. For the calculations necessary to know the weight of the objectives, which in this example is known in advance. It constitutes a cognitive map that displays local mutual goals. We calculate the degree of accessibility local purposes, according to the formula presented in the article. Then we have to minimize the number of local objectives for a particular algorithm.

Keywords: Minimizing local purposes, multicriteria optimization, expert evaluation, selecting a set of alternatives.

Введение

Возьмем некое множество цели, которое необходимо минимизировать. В качестве примера возьмем производство азотной кислоты. В качестве целей выбрано два направления увеличение надежности производства и снижение стоимости продукции. Также в эти цели входят множество подцелей, древо подцелей представлено ниже.

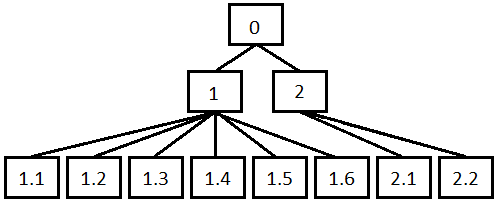
Рис. 1 - Дерево целей

За основу дерева берется нулевой уровень (Производство неконцентрированной азотной кислоты), следующий уровень это С₁ и С₂ и т.д.

В рамках целеполагания осуществляются поиск и изучение информации о системе и среде, в которой система функционирует, формируются основные (глобальные) цели и проводится их структурирование с выделением элементарных (локальных) целей. На основе экспертных оценок определяются рейтинги (сравнительная значимость) локальных целей и степень (уровень) их достижимости, зависящая от ограничений на потребляемые ресурсы. Формальными методами осуществляется минимизация числа локальных целей. Исходя из заданной степени достижимости глобальной цели, формируется множество возможных альтернатив целевых решений. Таким образом, осуществляется на базе отобранных локальных целей с учетом уровня их достижимости, и из их числа выбирается оптимальная альтернатива.[1]

Необходимо уменьшить число локальных целей, полный список целей представлен в таблице 1.

Таблица 1

Обозначение	Содержание	Вес цели
C0	Производство неконцентрированной азотной кислоты	1
C1	Надежность ХТС	0,75
C1.1	Уменьшить среднее время восстановления после отказа	0.049
C1.2	Уменьшить интенсивность отказов	0.082
C1.3	Резервирование элементов	0.043
C1.4	Разработка и внедрение способов прогнозирования неисправностей	0.246
C1.5	Применение высоконадежных элементов и оптимизация режимов их работы	0.082
C1.6	Упрощение системы	0.246
C2	Стоимость продукции	0,25
C2.1	Снизить транспортные расходы	0,19
C2.2	Внедрить новые технологии	0,06

 

Когнитивная карта

Для минимизации локальных целей необходимо рассчитать вес цели, в данном примере они нам известны. Составляем когнитивную карту взаимовлияния локальных целей (таблица 2). Данную таблицу должен составить эксперт по шкале от 0 до 1, где 1 – абсолютное влияние, 0,5 – среднее значение, 0 – отсутствие влияния. Так же допустимы промежуточные значения, такие как 0,1;0,2;0,3;0,4;0,6;0,7;0,8;0,9 в зависимости от степени влияния.

Пример когнитивной карты, отображающей взаимовлияние локальных целей.

Таблица 2

	C1.1	C1.2	C1.3	C1.4	C1.5	C1.6	C2.1	C2.2	Вес цели
C1.1	+1	+0,7	-0,2	+0,3	+0,6	+0,7		+0,5	0.049
C1.2	+0,7	+1	-0,5	+0,8	+0,7	+0,6		+0,5	0.082
C1.3	-0,7	0,6	+1			-0,7			0.043
C1.4	+0,5	+0,7		+1				+0,5	0.246
C1.5	+0,8	+0,8			+1			+0,3	0.082
C1.6			-0,5			+1			0.246
C2.1							+1		0,19
C2.2				+0,5	+0,5			+1	0,06

 

Строки и столбцы таблицы соответствуют локальным целям, слева от строки проставляется обозначение цели C_i, справа - ее вес W_i. На пересечении строки C_i и столбца C_j (i, j = 1, ..., N) записывается экспертная оценка +S_i,j, если достижение цели C_i усиливает достижение цели C_j , и оценка –S_i,j , если, наоборот, ослабляет. Коэффициент S_i,j, где 0 < S_i,j< 1, отражает силу воздействия цели C_i на цель C_j, например, так, как показано на шкале оценки взаимовлияния целей. Если цели не влияют друг на друга (S_i,j = 0) либо характер их взаимодействия неизвестен, то клетку (C_i, C_j) таблицы оставляем пустой.[1]

Степень достижимости

Для определения степени достижимости глобальной цели J(C₀) следует к каждому j-м столбце табл. 2 просуммировать произведения экспертной оценки в клетке (i, j) на вес строки W_i и затем сложить полученные величины по всем столбцам.

    (1)

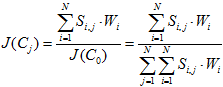    (2)

Степень достижимости локальной цели J(C_j) определена как отношение указанной суммы произведений для j-то столбца к величине J(C₀).

Вычисление произведения веса цели S_i,j можно представить в виде таблицы 3.

Таблица 3

	C1.1	C1.2	C1.3	C1.4	C1.5	C1.6	C2.1	C2.2	Вес цели
C1.1	0,049	0,034	-0,01	0,015	0,029	0,034	0	0,025	0.049
C1.2	0,057	0,082	-0,04	0,066	0,057	0,049	0	0,041	0.082
C1.3	-0,03	0,026	0,043	0	0	-0,03	0	0	0.043
C1.4	0,123	0,172	0	0,246	0	0	0	0,123	0.246
C1.5	0,066	0,066	0	0	0,082	0	0	0,025	0.082
C1.6	0	0	-0,12	0	0	0,246	0	0	0.246
C2.1	0	0	0	0	0	0	0,19	0	0,19
C2.2	0	0	0	0,03	0,03	0	0	0,06	0,06

 

Далее просуммируем столбцы и в итоге получим  J(C₀).

J(C₀)=0,2649+0,3799-0,1308+0,3563+0,1988+0,2994+0,19+0,2731=1,8316

В рассматриваемом примере (см. табл. 2) J(C₀) = 1,8, а значения J(C_j) приведены в табл. 4.

Выбранные локальные цели

Таблица 4

Cj	C1.1	C1.2	C1.3	C1.4	C1.5	C1.6	C2.1	C2.2
J(Cj)	0,145	0,207	-0,07	0,195	0,109	0,163	0,104	0,149
ej	e1	e2	–	e3	–	e4	–	e5

 

Множество всех локальных целей обозначим через С, подмножество удаляемых целей - через С*, а его мощность - через |С*|.

Степень достижимости подмножества целей С* = {C_j1, ..., C_jk} с учетом их взаимовлияния определяется соотношением

J(C*) = J(C_j1)+...+ J(C_jk)   (3)

Максимально допустимое значение J(С*) обозначим через D.

Минимизация числа локальных целей

Задачу минимизации сформулируем следующим образом:

найти С*   С такое, чтобы совместно выполнялись условия:

J(С*)≤ Д, (4) |С*| = max. (5)

Выбор наиболее значимых локальных целей системы осуществляется путем удаления наименее значимых из множества локальных целей.

При минимизации числа локальных целей должно совместно выполняться несколько условий:

• необходимо учитывать взаимное влияние локальных целей, отображаемое матрицей - когнитивной картой;
• суммарная степень достижимости удаляемых целей, имеющая численное выражение и определяемая на основе когнитивной карты, не должна превышать допустимого порогового значения;
• число удаляемых локальных целей должно быть максимально.[1]

Минимизацию числа локальных целей будем проводить на основе следующего алгоритма.

1. В множестве С выбрать цель С_j1 с минимальной степенью достижимости (J(С_j1) = min). Если таких целей более одной, то из них выбрать любую. Включить выбранную цель в подмножество С* и увеличить его степень достижимости J(С*) = J(С*) + J(C_j1).
2. Проверить условие (4). Если оно выполняется, то удалить С_j1 из С и перейти к шагу 1. Если условие (4) не выполняется ни для одной цели с J(C_j1) = min, т.е. к С* нельзя присоединить ни одной цели, то закончить алгоритм.

Работа алгоритма наглядно иллюстрируется в виде цепочки членов, соединенных стрелками. В числителе члена указывается состояние (состав) подмножества С* на данном шаге минимизации, в знаменателе - соответствующая степень достижимости J(С*).[1]

Заключение

В результате вычисления алгоритма отсеиваются незначительные локальные цели, после чего можно выделить оставшиеся цели. В данном примере принято, что  D = 0,25 и цепочка имеет вид:

Цели, вошедшие в состав подмножества С*, отмечаем в нижней строке табл. 4 прочерками, оставшиеся цели обозначаем символами е., i - 1, ..., N*, где

N* =N-|С*|  (6)

В нашем примере результатом минимизации числа локальных целей системы является множество Е = {e₁ е₂, е₃, е₄, e₅}, где

e₁ – уменьшить среднее время восстановления после отказа;

е₂ – уменьшить интенсивность отказов;

е₃ – разработка и внедрение способов прогнозирования неисправностей;

е₄ – упрощение системы;

e₅ – внедрить новые технологии;

Таким образом, данная методика минимизации локальных  целей позволит выделить приоритет развития предприятия и уменьшить большое число локальных целей. В данном примере экспертная оценка не проводилась, необходимо было показать методику минимизации локальных целей.

Литература

1. Юдицкий С.А., Владислав П.Н. Основы предпроектного анализа организационных систем: учебное пособие. – М.: Финансы и статистика, 2005. – 144 с.
2. Анкудинов Г.И., Анкудинов И.Г., Иванова И.В., Принятие решений в системном проектировании: Учебник. – СПб: Национальный минерально-сырьевой университет «Горный», 2013. – 176 с.
3. Ларичев О.Н. Теория и методы принятия решений, а также Хроника событий в Волшебных странах: Учебник. ­­– М.: Логос, 2000. – 296 с.
4. Лотов. А.В., Поспелова И.И., Многокритериальные задачи принятия решений: Учебное пособие. – М.: МАКС Пресс, 2008. – 197 с.
5. Черноморов Г.А. Теория принятия решений: Учебное пособие. Новочеркасск: Ред. журн. «Изв. вузов. Электромеханика», 2002.– 276 с.

References

1. Judickij S.A., Vladislav P.N. Osnovy predproektnogo analiza organizacionnyh system [Basics of pre-analysis of organizational systems]: Textbook. – M.: Finansy i statistika, 2005. – P. 144. [in Russian]
2. Ankudinov G.I., Ankudinov I.G., Ivanova I.V., Prinjatie reshenij v sistemnom proektirovanii [Decision-making in the system design]: – SPb: Nacional'nyj mineral'no-syr'evoj universitet «Gornyj», 2013. – P. 176. [in Russian]
3. Larichev O.N. Teorija i metody prinjatija reshenij, a takzhe Hronika sobytij v Volshebnyh stranah [Theory and methods of decision-making, as well as the chronicle of events in a magical land]: Textbook. – M.: Logos, 2000. – P. 296. [in Russian]
4. A.V., Pospelova I.I., Mnogokriterial'nye zadachi prinjatija reshenij [Multicriteria decision making problems]: Textbook. – M.: MAKS Press, 2008. – P. 197. [in Russian]
5. Chernomorov G.A. Teorija prinjatija reshenij [Decision theory]: Textbook. Novocherkassk: Red. zhurn. «Izv. vuzov. Jelektromehanika», 2002.– P. 276. [in Russian]