МЕТОД ОБРАБОТКИ ЭЛЕКТРОКАРДИОСИГНАЛОВ КОМПЕНСИРУЮЩИЙ ДРЕЙФ ИЗОЛИНИИ НА ОСНОВЕ МЕТОДА РЕГУЛЯРИЗАЦИИ

Горохов С.Н.¹, Щербакова Т.Ф.², Галимзянов Э.Р.³

¹ORCID:0000-0001-6152-9483, кандидат технических наук, доцент, ²кандидат технических наук, доцент, ³старший преподаватель, Казанский национальный исследовательский технический университет им. А.Н. Туполева-КАИ

МЕТОД ОБРАБОТКИ ЭЛЕКТРОКАРДИОСИГНАЛОВ КОМПЕНСИРУЮЩИЙ ДРЕЙФ ИЗОЛИНИИ НА ОСНОВЕ МЕТОДА РЕГУЛЯРИЗАЦИИ

Аннотация

В статье рассмотрен метод обработки медицинских диагностических сигналов, повышающий достоверность их анализа. Проведен анализ методов компенсации дрейфа изолинии электрокардиосигнала с целью выявления наиболее эффективного. Описан разработанный метод обработки сигналов на основе метода регуляризации, позволяющий эффективно подавлять низкочастотные помехи. Представлены результаты сравнения с другими известными методами оценки информационных параметров ST-сегмента электрокардиограммы. Данные результаты показывают повышение точности оценки параметров, полученных с помощью предложенного метода.

Ключевые слова: электрокардиосигнал, модель ЭКС, дрейф изолинии, фильтрация электрокардиосигнала, интерполяция.

Gorohov S.N.¹, Scherbakova T.F.² Galimzyanov E.R.³

¹ORCID:0000-0001-6152-9483, PhD in Engineering, associate professor, ²PhD in Engineering, associate professor, ³Senior Lecturer, Kazan National Research Technical University named after A.N.Tupolev – KAI

METHOD OF ELECTROCARDIOSIGNAL PROCESSING FOR COMPENSATING DRIFT ISOLINES BASED ON THE REGULARIZATION METHOD

Abstract

The article proposes method of processing medical diagnostic signals, which increases the accuracy of the analysis. The article compares the drift compensation techniques to identify the most effective. The developed signal processing method based on the method of regularization, which allows you to effectively suppress low-frequency noise is described. The article presents the results of the comparison with other known methods for calculating information parameters of ST-segment. These results indicate improved accuracy parameter estimates obtained using the proposed method.

Keywords: electrocardiosignal, ECS model, isoline drift, electrocardiosignal filtering, interpolation.

Сердечно-сосудистые (ССЗ) заболевания являются самой распространенной причиной смертности во всем мире. В связи с этим актуальна задача автоматического анализа электрокардиосигнала, в частности, для обнаружения ишемической болезни сердца человека (ИБС), являющаяся важным аспектом своевременной диагностики состояния ССЗ.

Для диагностики ССЗ на раннем этапе, необходимо иметь точные кардиологические данные по пациенту. В настоящее время основной проблемой получения точных данных о параметрах электрокардиосигнала (ЭКС) является наличие помех. Несомненно, самая трудноустраняемая помеха – это дрейф изолинии (ДИ) ЭКС. Связано это с тем доказанным фактом, что частотный спектр ДИ полностью перекрывается с частотным спектром ЭКС.

К появлению ДИ на ЭКС может привести:

- движения пациента во время съема ЭКС;

- нарушение контакта электрода и кожи пациента;

- значительное потоотделение.

При проведении велоэргометрических тестов ДИ приводит к усложнению автоматической обработки  ЭКС. В этом случае повышается роль фильтрации верхних частот по сравнению с обычными измерениями электрокардиограммы (ЭКГ). Если при спокойном мониторировании ЭКГ низкочастотный дрейф изолинии невелик по амплитуде и сосредоточен на частотах 0.01-0.2 Гц, то в велоэргометрии ситуация меняется. Амплитуда низкочастотной помехи может превышать величину R-зубца, а ее рабочий интервал частот увеличивается до 10 Гц.

Стандартными методами проектирования цифровых фильтров подавить ДИ без искажения формы ЭКС не представляется возможным, поэтому на практике чаще применяют методы компенсации ДИ во временной области.

Методы компенсации во временной области основаны на выделении сигнала низкочастотной помехи из смеси ЭКС и помехи с помощью интерполяционных методов. К таким методам можно отнести: кусочно-линейную интерполяцию, глобальную сплайн-интерполяцию, полиноминальную интерполяцию и др.

Однако интерполяции присущи существенные недостатки, а именно:

1) значительная чувствительность к высокочастотным помехам (шумы квантования, импульсные помехи).

2) ограниченность частотного диапазона устраняемой помехи.

При этом погрешность аппроксимации является методической и не устраняется. Выделение опорных точек, расположенных на изолинии, чаще всего затрудненно из-за сильного уровня помех. При увеличении частоты изменения сигнала ДИ ухудшается и точность его восстановления. Восстановление сигнала становится невозможным уже при достижении половины частоты следования опорных точек, равной ЧСС.

Для выделения сигнала ДИ предлагается фильтрационный метод, основный на использовании метода регуляризации, причем в качестве минимизирующего функционала предлагается использовать суммарное квадратичное отклонение сигнала, после вычета ДИ, выделенного с помощью метода регуляризации, от модельного сигнала, с оцененными параметрами.

В качестве модели элементов ЭКС используется экспоненциальная модель кардиосигнала [1,2]:

,

(1)

где  — амплитуда зубца,  — временное положение зубца,   — коэффициенты масштаба левого и правого «плеч» зубца соответственно.

При использовании данной модели для каждого элемента (зубца) кардиосигнала необходимо определить четыре параметра:  , , . Методика расчета данных параметров на примере зубца R описана в работе [4].

Аналогично производится оценка параметров Т зубца и формируется вектор параметров T зубца .

Если рассмотреть разность реального ЭКС и модели с оцененными параметрами, то суммарная спектральная мощность такой разности будет составлять 5-7% от мощности исходного ЭКС. При динамической нагрузке в велоэргонометрии к ЭКС добавляется низкочастотный шум и суммарная мощность разности сигналов может увеличиться до 30%.

Таким образом, задача сводится к минимизации функционала:

,

(2)

где  - исходный сигнал, после вычета ДИ, выделенного на основе метода регуляризации при конкретном ,  – модель сигнала с оцененными параметрами.  - длительность кардиоцикла.

Задача минимизации функционала (2) сводится к поиску безусловного экстремума функционала:

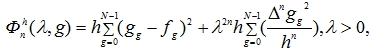(3)

где  - постоянный неопределенный множитель,

- выделенный ДИ.

При больших λ в функционале  определяющим является второе слагаемое, нижняя граница которого достигается на гладкой функции. Тогда, есть основания ожидать, что при некотором значении  функция g_g будет обеспечивать минимизацию функционала .

Имеем систему уравнений относительно значений g_g в точке экстремума:

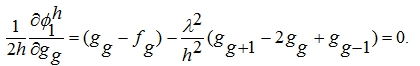
Пусть

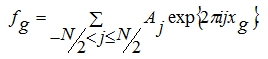
Будем искать  в виде

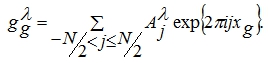
Вычислим оператор второй разности от функции :

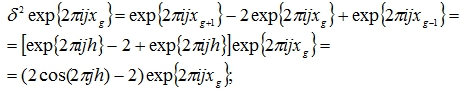
тогда

Подставим  после преобразования в виде суммы Фурье, а затем, преобразуем вторую разность , приведем подобные члены и получим

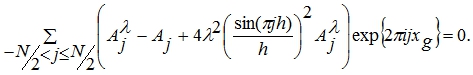
Это равенство удовлетворяется при

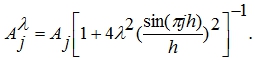
Следовательно,

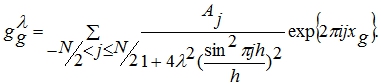
При каждом фиксированном λ величина  определяется с помощью решения системы линейных уравнений. При некотором значении  функция  будет обеспечивать минимизацию функционала .

Для подтверждения правильности теоретических выводов проводились экспериментальные проверки теоретических положений с использованием реальных электрокардиосигналов из стандартной базы ЭКГ-данных ресурса PhysioNet (СШA).

С помощью предложенного метода был проведен анализ ST-сегмента у 115 пациентов. Смещение сегмента ST отмечено у 25% пациентов.

Реализация алгоритма дала значительное уменьшение погрешности определения смещения ST-сегмента – 4,66±0,40 мкВ для предложенного метода при доверительной вероятности P=0,95. против 10,05±0,48 мкВ для метода глобальной сплайн-аппроксимации при доверительной вероятности P=0,75.

В результате применения предлагаемого алгоритма доверительный интервал оценки смещения ST-сегмента уменьшился в среднем на 17% по сравнению со стандартным алгоритмом при доверительном интервале вероятности данного события [0,87 .. 0,97].

При этом для предлагаемого метода достоверность диагностики состояния сердца о наличии или отсутствии ИБС составила не менее 0,95, в отличие от метода глобальной сплайн-аппроксимации – 0,75.

Предложенный метод коррекции ДИ обеспечивает более высокую точность определения информативных параметров ST-сегмента, чем существующие и имеет при этом надежную реализацию в системах применяющих автоматическую обработку ЭКС. Метод может быть использован в автоматических системах обработки ЭКС, для более точного измерения информационных параметров кардиоциклов ЭКС [3].

Список литературы / References

1. Абрамов М.В. Аппроксимации экспонентами временного кардиологического ряда на основе ЭКГ // Вестник кибернетики. – 2010. – №9. - С. 85-91.
2. Галимзянов Э.Р. Оптимизация метода выделения низкоамплитудных потенциалов с использованием модели электрической активности сердца // Биомедицинская радиоэлектроника. - 2012. - № 11. - С. 49-54.
3. Классификация P-зубца и QRS-комплекса электрокардиосигнала в рамках корреляционной теории для задач обнаружения аритмий сердца / Галимзянов Э.Р., Козлов С.В., Хомяков А.В. и др. // Инфокоммуникационные технологии. - 2012. - Т.10. - №2. - С. 59-64.
4. Горохов С.Н., Галимзянов Э.Р. Корреляционный метод обработки электрокардиосигнала для построения устройства анализа аритмий // Международный научно-исследовательский журнал. - 2016. - Часть 3. - №8. - С. 36-38.

Список литературы латинскими символами / References in Roman script

1. Abramov M.V. Approksimacii jeksponentami vremennogo kardiologicheskogo rjada na osnove EKG [Approximations using exponents of time cardiological series basing on ecg] // Vestnik kibernetiki [Cybernetics Bulletin]. – 2010. – №9. - P. 85-91. [in Russian]
2. Galimzyanov E.R. Optimizacija metoda vydelenija nizkoamplitudnyh potencialov s ispol'zovaniem modeli jelektricheskoj aktivnosti serdca [Optimization of the method for allocation of low-amplitude potentials using heart electrical activities models] // Biomedicinskaja radiojelektronika [Biomedical electronics]. - 2012. - № 11. - P. 49-54. [in Russian]
3. Klassifikacija P-zubca i QRS-kompleksa jelektrokardiosignala v ramkah korreljacionnoj teorii dlja zadach obnaruzhenija aritmij serdca [The classification of p-wave and qrs-complex on electrocardiosignal within the correlation theory for heart arrhythmias detection] / Galimzyanov E.R., Kozlov S.V., Khomyakov A.V. et al. // Infokommunikacionnye tehnologii [Infocommunication technologies]. - 2012. - V.10. - №2. - P. 59-64. [in Russian]
4. Gorohov S.N., Galimzyanov E.R. Korreljacionnyj metod obrabotki jelektrokardiosignala dlja postroenija ustrojstva analiza aritmij [Correlation method of electrocardiosignal processing for building a arrhythmia analyzer] // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Research Journal]. - 2016. - Part 3. - №8. - P. 36-38. [in Russian]