О ГОМОТОПИЧЕСКОМ ПОДХОДЕ В ГЕОМЕТРИЧЕСКОМ МОДЕЛИРОВАНИИ

 Берзин Д.В.

Кандидат физико-математических наук, доцент,

Финансовый университет при Правительстве Российской Федерации, Москва

О ГОМОТОПИЧЕСКОМ ПОДХОДЕ В ГЕОМЕТРИЧЕСКОМ МОДЕЛИРОВАНИИ

Аннотация

Опубликовано много значимых работ, относящихся к геометрическим методам объемного моделирования. Но очень немногие исследования рассматривали топологический аспект. В данной работе мы кратко описываем базовые гомотопические методы в трехмерном моделировании.

Ключевые слова: информационные технологии, 3D моделирование, прикладная информатика, топология, компьютерная графика  

Berzin D.V.

PhD,  Associate Professor,

 Financial University under the Government of the Russian Federation, Moscow

ABOUT HOMOTOPIC METHODS IN GEOMETRIC MODELING

Abstract

There were published a lot of valuable research results on geometric 3D modeling. But very few investigations were done on topological aspect of the modeling. In this work we briefly talk about homotopy methods, that might be used in computer graphics and computer animation.

Keywords: Information Technology, 3D modeling, applied informatics, topology, computer graphics  

1. Введение

Понятия топологического пространства и гомеоморфизма являются фундаментальными в математике. Грубо говоря, гомеоморфизмы описывают деформации геометрических объектов, и понятие гомеоморфизма полезно для выявления важных свойств объектов, которые не меняются в результате данных деформаций. Такие свойства называются топологическими. В отличие от метрических, которые связаны с расстояниями между точками, углами между прямыми и т.д. Например, куб и пирамида различны с метрической точки зрения, но они гомеоморфны. Для многих задач тонкие метрические свойства объектов не слишком важны, и порой необходимо выявлять грубые топологические свойства.

Известно, что понятие многообразия в геометрии является фундаментальным. Структура и свойства гладких многообразий являются хорошим подспорьем для методов CAGD (Computer-aided geometric design) и CG (компьютерной графики). Например, гауссова кривизна и другие инварианты являются важными в геометрическом моделировании. Порой структура гладкого многообразия не является достаточной, и тогда полезно воспользоваться понятием симплициального комплекса или клеточного пространства [1,2]. Симплициальный комплекс может рассматриваться как триангулированный объект (являющийся многообразием, или не являющийся таковым). Клеточное пространство - это объект, построенный из своего рода примитивов - клеток и может рассматриваться как обобщение понятия гладкого многообразия.

Топология (в частности, гомотопическая топология) является важным разделом в математике [1,2]. Ее базовые понятия, которые можно использовать в пространственном моделировании, - это гомеоморфизм, гомотопия, симплициальный комплекс, а также клеточное пространство.

В работах [3,4] и [8,9] используется так называемый клеточный подход к 3D моделированию. Топологические подходы также задействованы в [5]. Авторы предложили инновационную методику, называемую "Топологическое соответствие", в которой схожести между моделями быстро, точно и автоматически (посредством информационных технологий) вычисляются путем сравнения их "мультиразрешающих реберных графов" (MRG). Между прочим, японский профессор Куни и его последователи активно используют теорию Морса и представление объектов в виде MRG в своих исследованиях [6,7].

2. Гомотопический подход

Понятие топологического пространства является центральным в топологии. Но оно - слишком общее. Почти всегда математика работает с пространствами, на которых введены дополнительные структуры: дифференциальная, риманова, симплектическая и т.д. Они весьма естественны. Во-вторых, могут быть добавлены комбинаторные структуры. Можно разложить объект на отдельные части и исследовать, как они расположены друг относительно друга. Важными комбинаторными структурами являются симплициальные и клеточные комплексы.

Пусть X, Y  - два топологических пространства. Отображение f : X→Y  называется гомеоморфизмом, если это - непрерывное и взаимно-однозначное соответствие, а обратное отображение f тоже непрерывно [1,2]. Два топологических пространства гомеоморфны, если между ними существует гомеоморфизм. Семейство отображений H(x,t) : X×[0,1] → Y называется гомотопией между X и Y, если оно непрерывно (одновременно по отношению к обоим параметрам). Два отображения гомотопны друг другу, если мы можем перейти от одного к другому посредством непрерывной деформации с параметром t из интервала [0,1]. Два топологических пространства X и Y являются гомотопически эквивалентными (или гомотопными), если существуют такие непрерывные отображения f : X→Y  и g : Y→X, что каждая из композиций fg : Y→Y  и gf: X→X  гомотопны идентичному отображению id: X→X.

Перечислим некоторые хорошо известные примеры гомотопически эквивалентных, но не гомеоморфных пространств: Евклидово пространство R и точка; лента Мебиуса и окружность; сфера с тремя дырками и букет из двух окружностей S¹ ∨S¹ ; окружность и кольцо. Последний случай проиллюстрирован на рис.1. Пусть f : S¹→S¹ - тождественное отображение, и h - это сжатие вдоль радиуса, и пусть g - это композиция g=f h.  Тогда fg и gf гомотопически эквивалентны соответствующим тождественным отображениям.

   

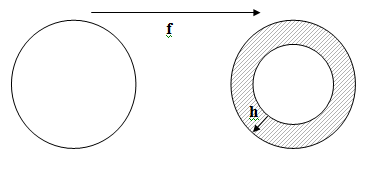
Рис. 1. Окружность и кольцо не гомеоморфны, но гомотопически эквивалентны

Пример не гомотопных многообразий: сфера и тор. Деформации (морфинги) реальных объектов часто могут быть рассмотрены как гомеоморфные или гомотопные, и в задачах компьютерной анимации и компьютерной графики  параметр t может рассматриваться как время. Данный математический подход предоставляет обширное поле для дальнейших исследований.

 

Литература

1. T. Fomenko, T. L. Kunii “Topological Modeling for Visualization” // Springer, 1998
2. T. Fomenko, D. B. Fuchs “Course of Homotopic Topology.” // Kluwer Academic Publishers
3. L. Kunii “Valid Computational Shape Modeling: Design and Implementation” // World Scientific, December 1999
4. Ohmori, T.L.Kunii “Shape Modeling Using Homotopy” // IEEE 2001.
5. Masaki Hilaga, Yoshihisa Shinagawa, Taku Kohmura, Tosiyasu L. Kunii (2001). Topology Matching for Fully Automatic Similarity Estimation of 3D Shapes // SIGGRAPH’2001
6. Shinagawa, T. L. Kunii, Y. L. Kergosien “Surface Coding Based on Morse Theory” // IEEE Computer Graphics & Applications, 1991.
7. Shinagawa, T. L. Kunii “Constructing a Reeb Graph Automatically from Cross Sections” // IEEE Computer Graphics & Applications, 1991.
8. Dmitry Berzin "On homotopy and cellular approaches to shape modelling" // Международный научно исследовательский журнал = Research Journal of International Studies, №8 (27) 2014, p. 4
9. Dmitry Berzin "On topological methods in shape modelling" // Международный научно исследовательский журнал = Research Journal of International Studies, №9 (28) 2014, p. 7

References

1. T. Fomenko, T. L. Kunii “Topological Modeling for Visualization” // Springer, 1998
2. T. Fomenko, D. B. Fuchs “Course of Homotopic Topology.” // Kluwer Academic Publishers
3. L. Kunii “Valid Computational Shape Modeling: Design and Implementation” // World Scientific, December 1999
4. Ohmori, T.L.Kunii “Shape Modeling Using Homotopy” // IEEE 2001.
5. Masaki Hilaga, Yoshihisa Shinagawa, Taku Kohmura, Tosiyasu L. Kunii (2001). Topology Matching for Fully Automatic Similarity Estimation of 3D Shapes // SIGGRAPH’2001
6. Shinagawa, T. L. Kunii, Y. L. Kergosien “Surface Coding Based on Morse Theory” // IEEE Computer Graphics & Applications, 1991.
7. Shinagawa, T. L. Kunii “Constructing a Reeb Graph Automatically from Cross Sections” // IEEE Computer Graphics & Applications, 1991.
8. Dmitry Berzin "On homotopy and cellular approaches to shape modelling" // Research Journal of International Studies, №8 (27) 2014, p. 4
9. Dmitry Berzin "On topological methods in shape modelling" // Research Journal of International Studies, №9 (28) 2014, p. 7