Численное решение краевой задачи, описывающей конвективное течение вязкой несжимаемой жидкости в горизонтальном слое

Конвективные процессы играют важную роль в различных природных явлениях и технических приложениях, таких как атмосферные движения, океанские течения и теплообменные процессы. Они возникают из-за неравномерного распределения температуры и плотности в жидкостях и газах, вызывая движение вещества под воздействием гравитации. Понимание этих процессов необходимо для прогнозирования погодных условий, улучшения эффективности теплообменников и других инженерных устройств.

Моделирование конвекционных течений традиционно осуществляется с помощью уравнений Навье-Стокса и уравнения теплопроводности. Однако в случаях сложных течений, особенно при воздействии внешних факторов, таких как ветер, получение точного аналитического решения становится затруднительным. В связи с этим возрастает значимость численных методов для анализа таких задач.

Данная статья посвящена численному решению краевой задачи, описывающей конвективное течение вязкой несжимаемой жидкости в горизонтальном слое. Особое внимание уделено влиянию стратификации и сдвиговых течений на структуру потока и распределение полей скорости.

Ранее проведённые исследования показали важность учета стратификации и сдвиговых эффектов в моделях конвективных течений

Цель настоящего исследования заключается в сравнении численной методики для решения краевых задач, связанных с конвективными течениями в горизонтальных слоях жидкости, с ранее полученными аналитическими решениями. Результаты этой работы будут полезны для дальнейшего развития теории гидродинамики и её практических применений.

Рассматривается течение вязкой несжимаемой жидкости в горизонтальном слое постоянной толщины h. В отличие от изотермического случая

- уравнение Навье-Стокса в приближении Буссинеска:

- уравнение теплопроводности:

- уравнение несжимаемости жидкости:

Здесь Vx, Vy, Vz — компоненты скорости, параллельные соответствующим осям координат прямоугольной декартовой системы Oxy. Система координат введена так, что ось Oz направлена строго вверх. P = P(x, y, z) — отклонение давления от гидростатического, отнесённое к постоянной средней плотности жидкости ρ, T = T(x, y, z) отклонение температуры от средней, β — температурный коэффициент объемного расширения,

Имеются пять уравнений (1)-(3) и 4 неизвестных Vx, Vy, P, T. Такая система является переопределенной. Будем искать решение для ненулевых компонент вектора скорости (Vx, Vy) в виде

При подстановке представления (4) в уравнение несжимаемости (3) последнее удовлетворяется тождественно. Проблема с переопределением разрешена.

После несложных преобразований получаем итоговую систему уравнений:

В итоге система уравнений в частных производных (1)-(3) превращается в систему обыкновенных дифференциальных уравнений (5) для нахождения неизвестных функций  

Общее решение системы (5) представляет собой набор полиномиальных функций не выше четырнадцатой степени.

В решение системы (5) входят пятнадцать постоянных интегрирования, для их определения потребуются граничные условия. Будем рассматривать течение в слое жидкости толщины h, нижней границе которого соответствует значение z=0 вертикальной координаты. Положим, что на нижней границе выполняется условие прилипания, а также известно распределение температуры:

На верхней же границе (при z=h) положим известными распределение поля скорости, температуры и давления:

Здесь W — значение фоновой скорости течения жидкости на верхней поверхности слоя, угол характеризует направление вектора скорости по отношению к координатным осям Oxy, 

Численное решение задачи будет построено с помощью метода Рунге-Кутты четвертого порядка

Подробный анализ точного решения системы дифференциальных уравнений (5) для поля скорости был проведен и опубликован ранее

4.1. Анализ скорости v

Для удобства дальнейшего анализа нормируем вертикальную координату 

Начнем сравнительный анализ со свойств скорости 

где

а индекс i коэффициента 

Ранее при анализе точного решения были рассмотрены различные комбинации значений констант 

Случай I. Пусть 

Этот случай возможен, в частности, при 

Анализ аналитического решения показал, что наибольшее число внутренних (т. е. принадлежащих слою) застойных точек равняется двум, что проиллюстрировано на рис. 1. Как видно из графика, численное решение с такими краевыми параметрами дает хорошее совпадение с аналитическим решением (рис. 1).

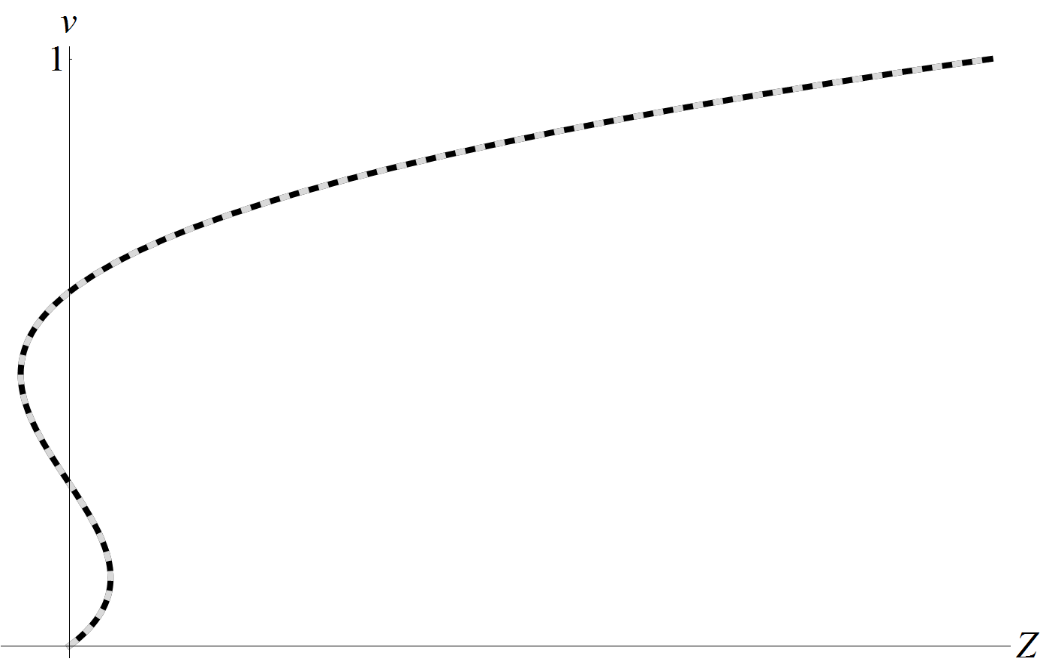
Рисунок 1 - Профиль скорости v при a5 = 0, a0a1a2 ≠ 0

Примечание: черная кривая – точное решение, серая пунктирная – численное решение

DOI:10.60797/IRJ.2025.160s.32.1

Случай II. Ни один из коэффициентов 

$a_i(i=0,1,2,5)$

не равен нулю.

Это наиболее общий случай из исследуемых. Он возможен, в частности, при 

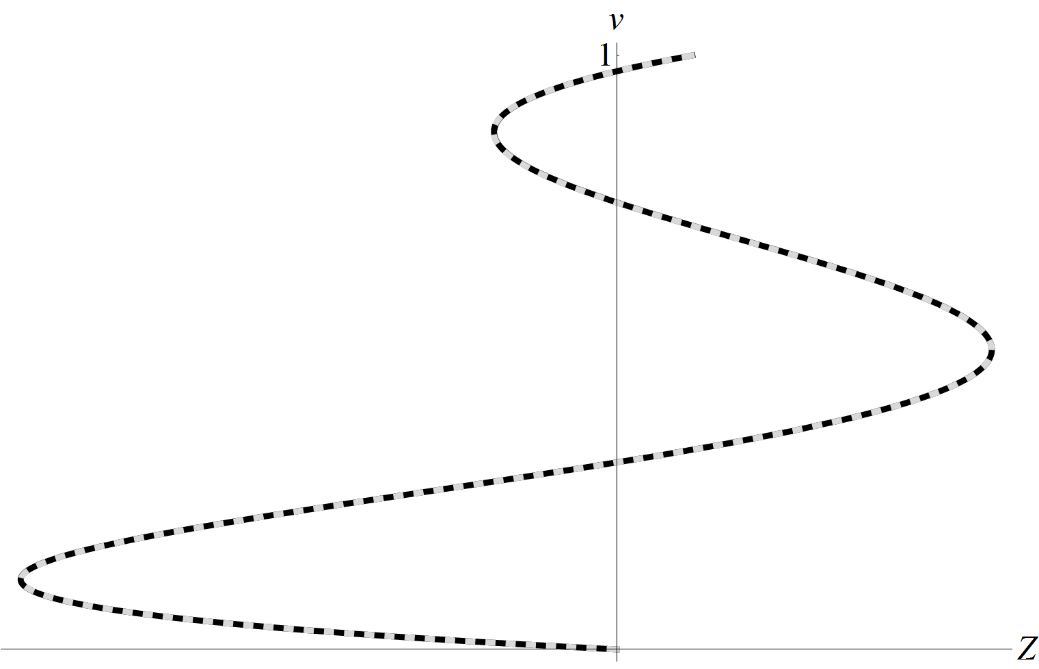
Рисунок 2 - Профиль скорости v при a0a1a2a5 ≠ 0

 

Примечание: черная кривая – точное решение, серая пунктирная – численное решение

DOI:10.60797/IRJ.2025.160s.32.2

Рассмотрев различные вариации значений параметров в аналитическом и численном решении для скорости 

$v$

, было показано, что компонента v вектора скорости может как не иметь нулей в рассматриваемом слое, так и иметь несколько (но не более трех) застойных точек внутри слоя, таким образом, разделяя его на четыре подслоя с возможной сменой направления течения (рис. 2). Метод Рунге-Кутты четвертого порядка

[13]

,

[14]

оказался достаточно точным, что подтверждается полным совпадением проиллюстрированных результатов.

4.2. Анализ скорости u

Перейдем к анализу компоненты u скорости 

Здесь введены следующие обозначения:

Рассмотрим общий случай выражения, когда все коэффициенты отличны от нуля 

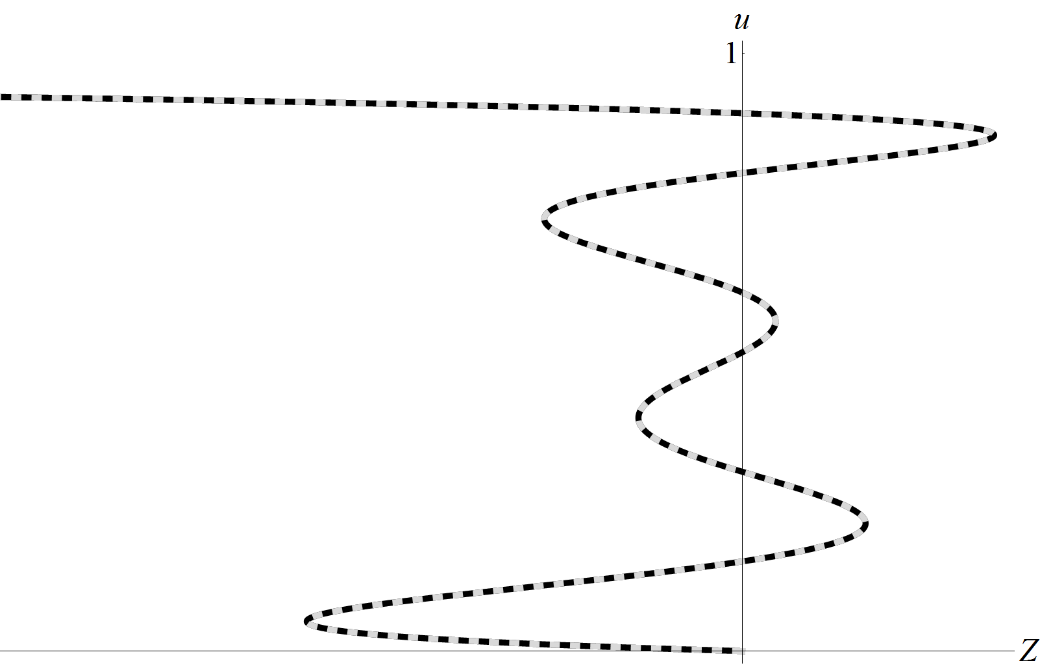
Рисунок 3 - Профиль скорости u при b0b1b2b3b4b5b8 ≠ 0

Примечание: черная кривая – точное решение, серая пунктирная – численное решение

DOI:10.60797/IRJ.2025.160s.32.3

В заключении отметим, что в данной работе был проведен комплексный анализ краевой задачи, описывающей конвективное течение вязкой несжимаемой вертикально завихренной жидкости в горизонтальном слое. Ранее в исследовании уже было детально изучено аналитическое решение данной задачи. В настоящей статье основное внимание уделено численному решению, полученному методом Рунге-Кутты четвертого порядка. Этот метод продемонстрировал высокую точность при решении исследуемой системы дифференциальных уравнений.

Было установлено, что в слое жидкости могут формироваться зоны с обратным течением, причем количество таких зон ограничено четырьмя подслоями с различным направлением течения. Важно отметить, что число застойных точек и, следовательно, количество подслоев, зависит от конкретных значений параметров краевой задачи.

Проведенное сравнение численного и аналитического решений показало согласованность результатов, что подтверждает надежность использованного численного метода для решения подобных задач. Таким образом, полученные результаты представляют собой важный вклад в изучение конвективных течений и могут служить основой для дальнейших исследований в этой области.