Электросопротивление бинарных антиферромагнитных сплавов
Электросопротивление бинарных антиферромагнитных сплавов
Аннотация
Электрическое сопротивление антиферромагнитных сплавов рассчитано в приближении когерентного потенциала. Показано, что если энергия Ферми локализована вблизи щели в плотности электронных состояний, то электрическое сопротивление может возрастать с ростом намагниченности подрешеток. Экспериментальные исследования, проведенные ранее для сплавов Cr-Pt, показывают, что при возрастании концентрации примеси аномалия сопротивления увеличивается. Для сплавов Ni-Mn эквиатомного состава ранее было экспериментально обнаружено значительное увеличение электросопротивления (свыше 80%) при переходе в АФМ состояние. Таким образом, предложенная нами теория позволяет качественно объяснить наблюдавшиеся температурные и концентрационные аномалии электросопротивления АФМ сплавов.
1. Введение
Как известно, при атомном упорядочении бинарных и тройных немагнитных сплавов происходит перестройка электронного спектра. Для некоторых (но не для всех!) сплавов электросопротивление
В данной работе выполнен теоретический расчет высокотемпературного (
2. Остаточное электросопротивление бинарных антиферромагнитных сплавов
Предполагая, как это обычно делается в ПКП, что энергии электронного переноса между различными узлами не зависят от состава сплава, и используя
В этой формуле
Имея в виду использование одноузельного варианта ПКП , , представим H в виде
где
В соответствии со сверхструктурой АФМ сплава введем оператор когерентного потенциала
через который выразим эффективный гамильтониан сплава
и соответствующую ему одноэлектронную функцию Грина
Условие самосогласования одноузельного ПКП, из которого находится оператор когерентного потенциала, состоит в равенстве нулю усредненной t -матрицы рассеяния
Здесь символ означает тепловое усреднение в системе локализованных спинов при фиксированной конфигурации атомов в сплаве, которое далее проводится в приближении молекулярного поля, а символ <...> означает усреднение по всем возможным конфигурациям при заданном значении концентрации компоненты А. Для случайной одноузельной величины
При вычислении тепловых средних в системе локализованных спинов для АФМ сплава запишем
где
Тогда плотность электронных состояний
Таким образом и в антиферромагнитных сплавах и в чистых антифер-ромагнетиках при
В пределе слабого рассеяния (вторая итерация) недиагональные по спину матричные элементы когерентного потенциала равны нулю, а диагональные могут быть записаны в виде
Тензор статической электропроводности сплава определяется по формуле Кубо-Гринвуда
где
Формулу (18) можно записать в виде
где
Поскольку величины, входящие в (20), являются трансляционно-инвариантными, вычисляем шпур в блоховском базисе. Используя для получающейся при этом суммы по
В этом случае проводимость будет отлична от нуля тогда, когда энергия Ферми сплава попадает в интервал
и результаты будут существенно зависеть от локализации энергии Ферми относительно щели.
3. Основные результаты и их обсуждение
Если энергия Ферми расположена вдали от щели, электросопротивление антиферромагнитного сплава есть
Видно, что сопротивление является линейно-квадратичной функцией состава, и переход в антиферромагнитное состояние, сопровождающийся увеличением спонтанной намагниченности подрешеток, приводит к уменьшению
Если энергия Ферми находится вблизи от щели, сопротивление описывается более сложным выражением
где
Отметим, что выражения (22)-(26) получены в приближении, сохраняющем наибольший член разложения по параметрам рассеяния.
В парамагнитной области (
В этом случае сопротивление является суммой вкладов от упругого спинового рассеяния и упругого примесного рассеяния.
Изменение
В отличие от
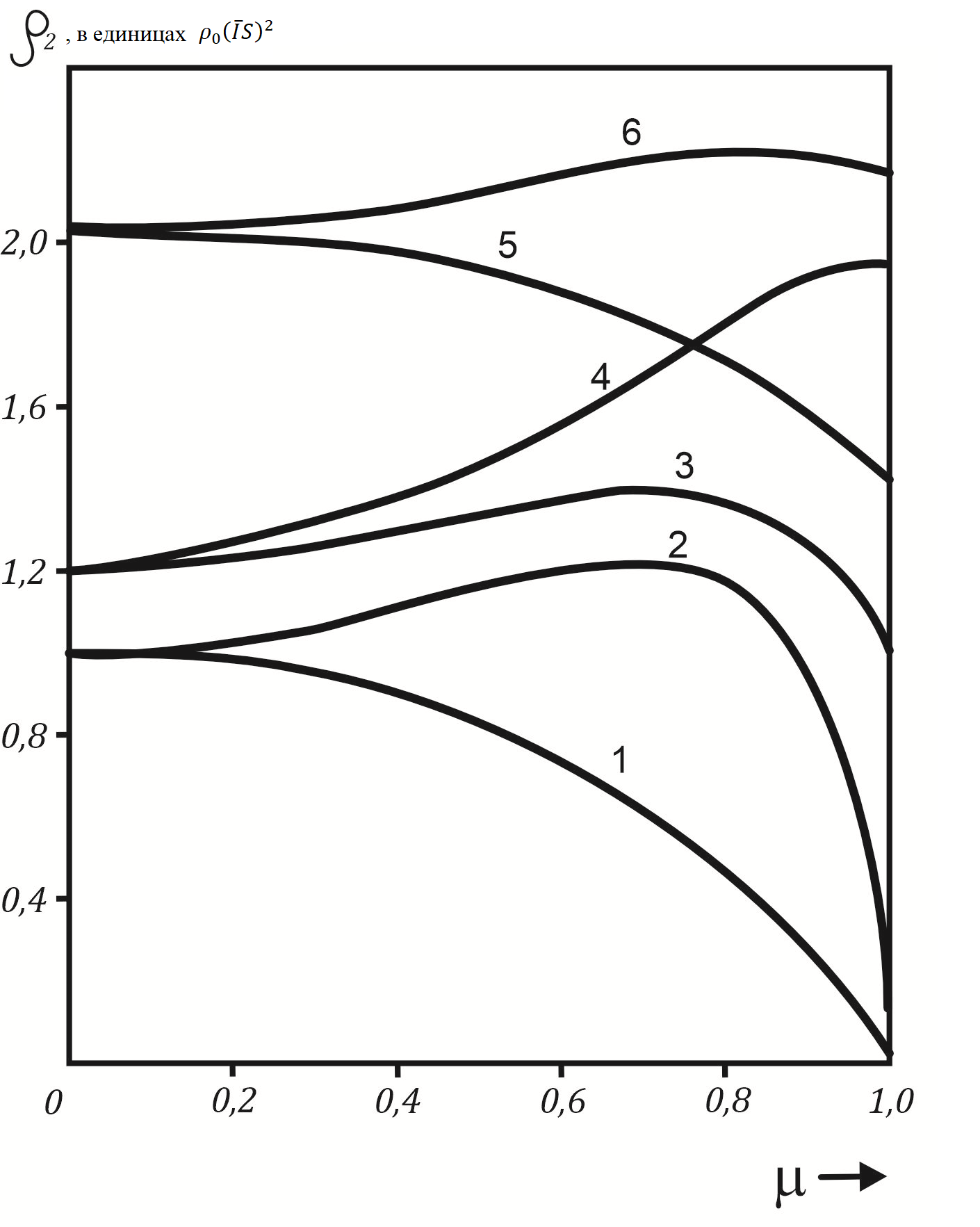
Рисунок 1 - Зависимость p2 от намагниченности подрешетки для различных значений параметров |τ| и a:
(1) |τ|=0,4, a=1; (2) |τ|=0,9, a=1; (3) |τ|=0,8, a=1,2;
(4) |τ|=0,9, a=1,2; (5) |τ|=0,4, a=2; (6) |τ|=0,6, a=2
Концентрационная зависимость слагаемого
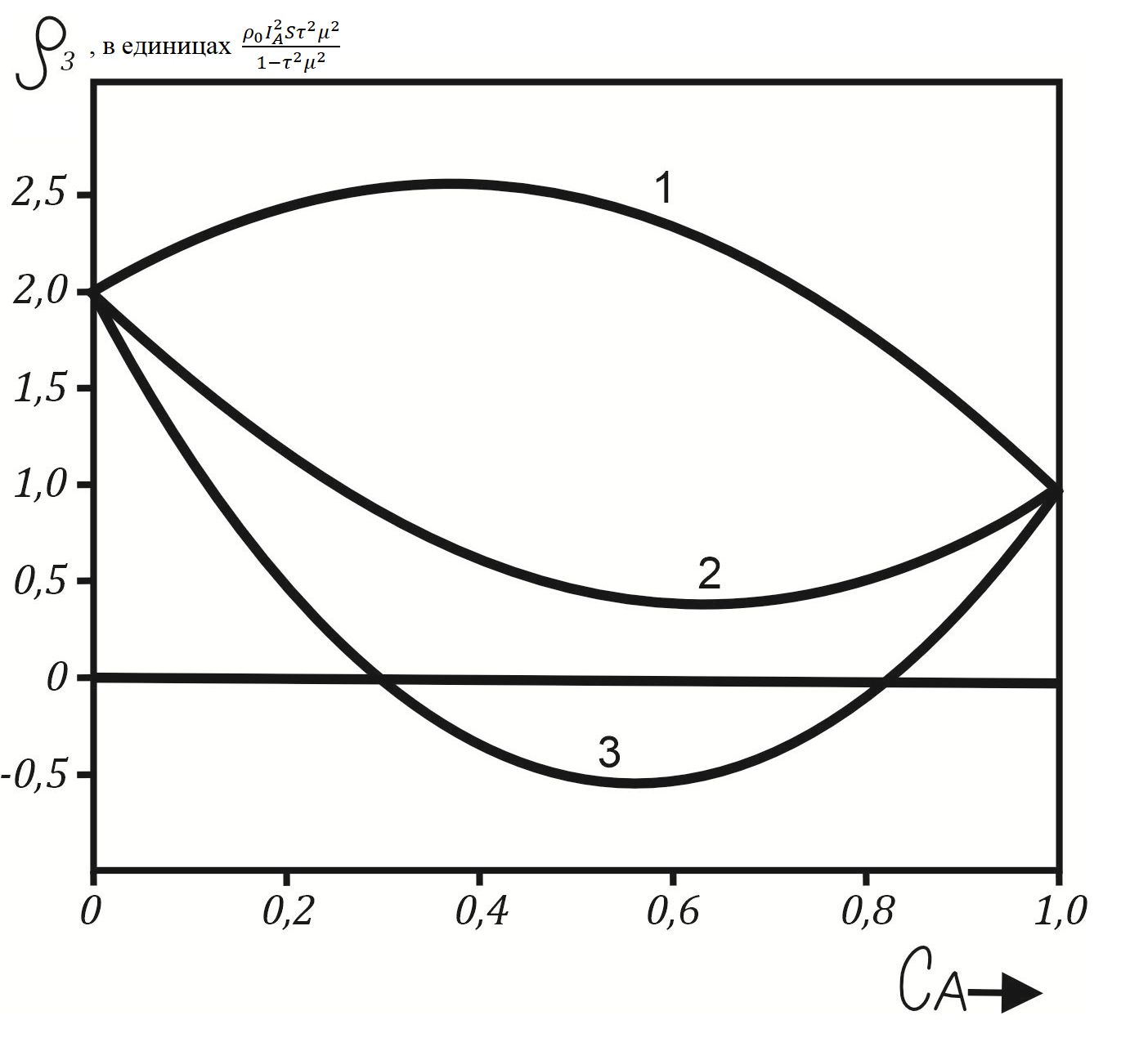
Рисунок 2 - Концентрационная зависимость ρ3 для ряда значений параметра b:
(1) b= 4; (2) b= - 4; (3) b= - 8
4. Заключение
Экспериментальные исследования
, проведенные для сплавов Cr-Pt, показывают, что при возрастании концентрации примеси аномалия сопротивления увеличивается. В для сплавов Ni-Mn эквиатомного состава было обнаружено значительное увеличение электросопротивления (свыше 80%) при переходе в АФМ состояние. В свете изложенной теории представляется возможным связать эти факты с вкладом слагаемогоТаким образом, изучение примесного и спинового рассеяния позволяет качественно объяснить наблюдавшиеся температурные и концентрационные аномалии электросопротивления АФМ сплавов.
