КОНЕЧНО-РАЗНОСТНАЯ СХЕМА ЭЙЛЕРА ПЕРВОГО ПОРЯДКА ТОЧНОСТИ ДЛЯ МОДЕЛИРОВАНИЯ ОДНОМЕРНОГО СТАЦИОНАРНОГО ТЕЧЕНИЯ ПОРОШКОВОЙ СРЕДЫ
КОНЕЧНО-РАЗНОСТНАЯ СХЕМА ЭЙЛЕРА ПЕРВОГО ПОРЯДКА ТОЧНОСТИ ДЛЯ МОДЕЛИРОВАНИЯ ОДНОМЕРНОГО СТАЦИОНАРНОГО ТЕЧЕНИЯ ПОРОШКОВОЙ СРЕДЫ
Аннотация
Одним из направлений гидродинамики неоднородных сред является изучение течений неоднородных сред, в том числе течений газодисперсных сред с насыпной плотностью. В работе представлена численная модель одномерного стационарного движения порошковой среды. Математическая модель реализовывала континуальную методику динамики неоднородной среды. Для каждой из фаз порошковой среды решалась полная гидродинамическая система уравнений в одномерном стационарном приближении включавшая с себя уравнение неразрывности, уравнение сохранения импульса и уравнение сохранения энергии. Математическая модель учитывала взаимодействие между газовой и дисперсной фазы порошковой среды, включавшее в себя обмен импульсом и теплообмен. Обмен импульсом включал в себя нелинейную силу аэродинамического сопротивления.
1. Введение
Практическое применение теории динамики неоднородных сред затрагивает широкий перечень различных областей. В публикации разрабатываются трехмерные численные модели течений изотермальной вязкой ньютоновской многофазной жидкости на различных поверхностях под действием силы тяжести. В работе в связи с проблемами подводной нефтедобычи разработана математическая модель многофазной затопленной струи, математическая модель не предполагала интегрировании систем уравнений динамики сплошной среды. В монографиях , , предложены различные математические модели течений неоднородных сред.
В статье рассматривается неравновесное критическое изотермическое истечение порошково-газовой среды из конического канала. В публикации делается обзор работ, посвященных численному моделированию различных технологических процессов, связанных с псевдоожиженным слоем, рассматриваться различные подходы математического моделирования течений порошковых сред. В работе делается обзор промышленных технологий, имеющих в основе гидродинамические процессы псевдоожиженного слоя, высказывается предположение о важности математического моделирования такого рода течений. В исследовании представлен обзор исследований, направленных на увеличение эффективности установок сжигания твердой биомассы в псевдоожиженном слое. В работе в стационарной постановке моделировался процесс прямой газификации биомассы в реакторе с кипящим слоем. В статье теоретически исследуются процессы в кипящем псевдоосжиженном слое газа и твердых дисперсных сред. В публикации выполнен обзор методов численного моделирования гидродинамики сыпучих сред. В работе представлена численная реализация математической модели одномерного движения сыпучей среды. Математическая модель была разработана в рамках равновесной методики моделирования многофазных сред, без разделения дисперсной и газовой фаз порошковой среды и без учета взаимодействия фаз в процессе течения. В статье анализируются особенности гидродинамики псевдоожиженного слоя полидисперсных зернистых материалов в отличие от монодисперсных псевдоожиженных систем.
Новизна представленной в работе численной модели стационарного течения заключается в том, что математическая модель одномерного течения разработана на основе континуальной методики динамики многофазных сред, учитывающей межфазное взаимодействие, для каждой из компонент порошковой смеси решалась полная гидродинамическая система уравнений.
Целью данной работы было исследование физических параметров газовой и дисперсной фаз в ламинарном стационарном течении порошковой среды в канале с учетом межфазного взаимодействия и влияния энергии деформации дисперсной фазы порошковой среды.
В ходе достижения целей работы был решен ряд задач: разработана математическая модель стационарного течения порошковой среды, разработан конечно-разностный алгоритм численного решения системы нелинейных дифференциальных уравнений математической модели, а также разработана компьютерная программа, реализующая математическую модель.
2. Методы исследования
Динамика сплошной среды моделируется из предположения одномерности и стационарности моделируемого течения. Уравнения движения однородного невязкого сжимаемого газа будут иметь вид (1–3):
Из уравнения (1) следует, что стационарные одномерные течения имеют постоянный расход — ρu=const, в таком случае уравнение (2) может быть преобразовано к виду (4), где β0= ρu:
из уравнения (4) следует, что уравнение (3) имеет вид (5):
Несмотря на описанные выше упрощения, уравнение (5) является нелинейным и требует для интегрирования c помощью численных методов.
Для моделирования течений неоднородных сред может быть применен траекторный подход, описанный в работах , диффузионный подход и континуальный подход , . Континуальная математическая модель динамики порошковой среды , для сжимаемого стационарного течения имеет следующий вид (6)–(12):
Уравнения (6), (7) — уравнения неразрывности фаз смеси, уравнения (8), (9) — уравнения сохранения импульса несущей и дисперсной фаз смеси, уравнение (10) — уравнение сохранения тепловой энергии дисперсной фазы, уравнение (11) — уравнение сохранения кинетической энергии дисперсной фазы, уравнение (12) — уравнения сохранения полной энергии несущей среды.
Q(T,T1) — поток тепла между несущей средой и дисперсной фазы, F(u,u1) — функция обмена импульсом между фазами смеси. Здесь Nu1 — относительное число Нуссельта , d — диаметр частицы, ξ−коэффициент межгранулярного напряжения, σ — функция энергии деформации дисперсной фазы. Число Нуссельта определяется с помощью известной аппроксимации в зависимости от относительного числа Маха M1, относительного числа Рейнольдса Re1 и числа Прандтля Pr :
Исходя из условий сжимаемости стационарного потока, возможно предположить, что
Для получения численного решения использовалась конечно-разностная аппроксимация с шагом вперед (20)–(24):
Здесь Δx=L/(N-1), шаг конечно-разностного разбиения равный отношению длины отрезка моделируемого течения — L к количеству узлов конечно-разностного разбиения — N. Так как система уравнений (20)–(24) имеет нелинейный характер, то для решения конечно-разностных уравнений применялся метод Ньютона . Численный алгоритм решения системы нелинейных дифференциальных уравнений (20)–(24) реализован в виде компьютерной программы написанной на языке программирования Fortran.
3. Результаты расчетов
Параметры дисперсной фазы, физическая плотность материала — ρ10=2500 кг/м3, размер дисперсных включений — d=10 мкм, начальная объемная доля дисперсной фазы α10=0,1. Длина отрезка, на котором моделируется течение неоднородной среды — L=1 м. Количество узлов — N=200. Для несущей среды задавались физические параметры воздуха: молярная масса — М=29·10-3 кг/моль, теплопроводность газа — λ=0,02553 Вт/(м·К), динамическая вязкость — μ=1,72·10-5 Па·с, постоянная адиабаты – γ=1,4, газовая постоянная — R=8,31 Дж/(моль·K). Начальное давление газа — р0=100 кПа. Моделировалось течение порошковой среды на отрезке канала длиной L с начальным давлением р0. Начальная скорость несущей и дисперсной фаз порошковой среды составляли — u0=-4 м/c, u10=-4 м/c.

Рисунок 1 - Схематичное изображение течения
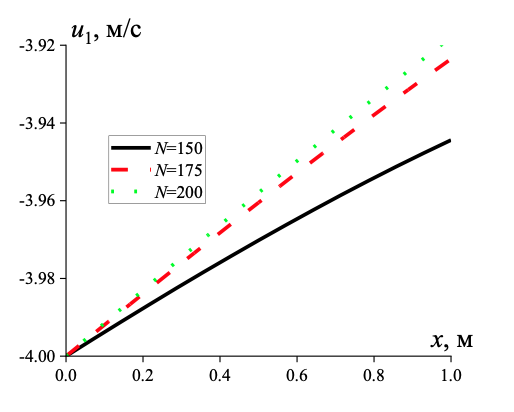
Рисунок 2 - Сопоставление расчетов скорости дисперсной фазы, проведенных для различного количества узлов
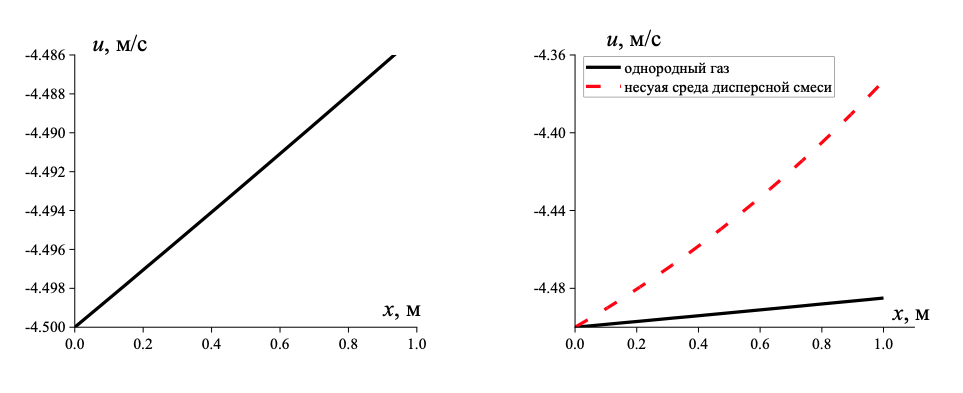
Рисунок 3 - Распределение скорости в однородном газе (а) и в газовой фазе порошковой среды (б)
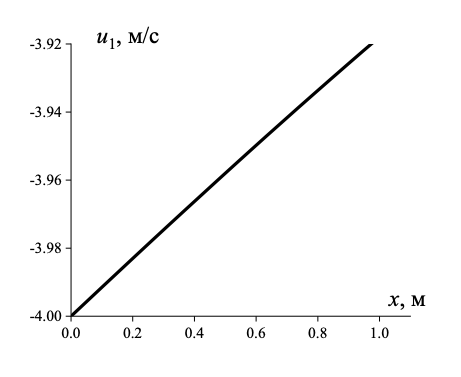
Рисунок 4 - Распределение скорости дисперсной компоненты
По мере движения в канале также по модулю убывает значение скорости дисперсной фазы порошковой среды — рисунок 4.
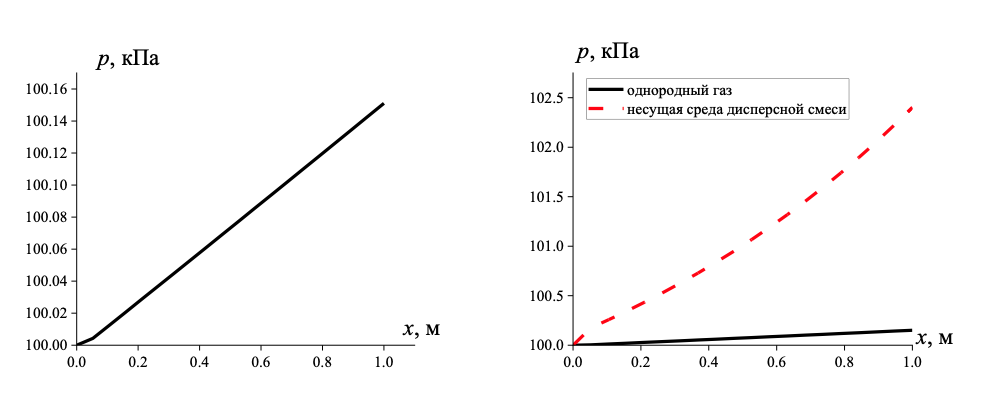
Рисунок 5 - Давление однородного газа (а) и газовой фазы порошковой среды (б)
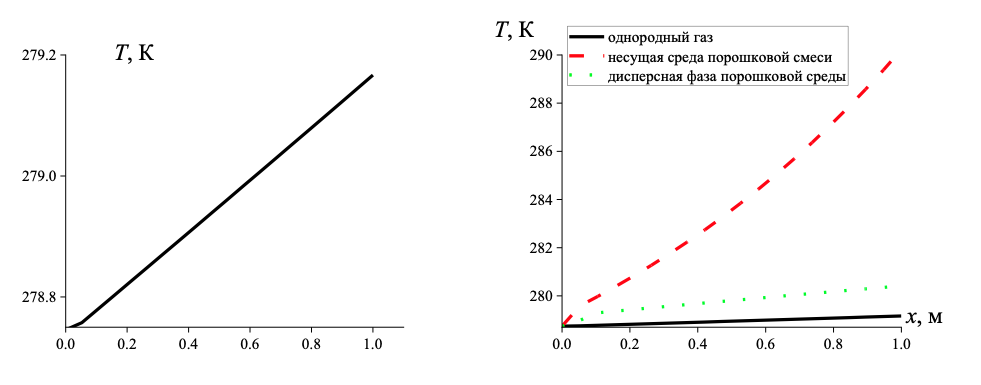
Рисунок 6 - Температура в однородном газе (а), температура компонент порошковой среды (б)
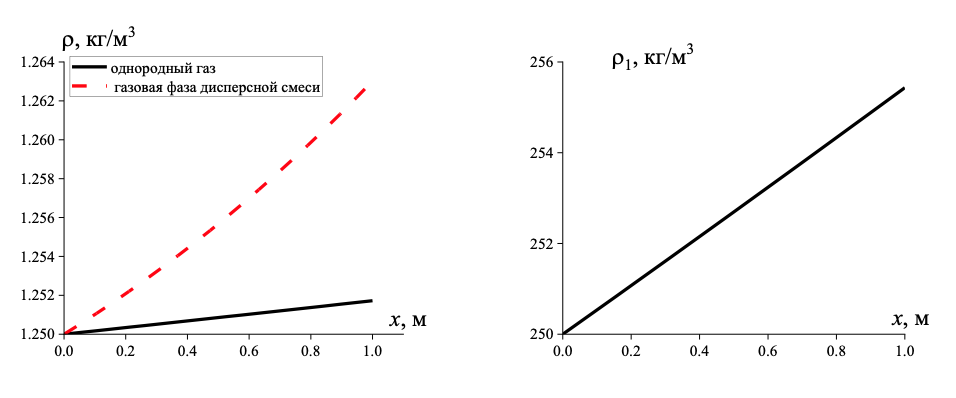
Рисунок 7 - Распределение плотности однородного газа и газовой фазы порошковой среды (а), плотности дисперсной фаз (б)
4. Заключение
Новизна представленных в работе расчетов заключается в том, что расчеты были проведены в рамках численной модели стационарного течения порошковой среды в канале, учитывающей не только межфазное взаимодействие несущей среды и дисперсной фазы, но и влияние напряжений деформации порошковой среды. Для реализации численной модели разработана компьютерная программа. Исследование сеточной сходимости конечно-разностной модели течения порошковой среды демонстрирует сходимость конечно-разностного алгоритма. Анализ результатов численных расчетов показывает, что при перепаде давления в 16 раз большем, чем в однородном газе скорость движения порошковой среды уменьшается примерно в 6,25 раз относительно уменьшения скорости на таком же отрезке канала в однородном газе.
