НЕКОТОРЫЕ ОБОБЩЕНИЯ КОНВЕКТИВНОЙ МОДЕЛИ ГЕНЕРАЦИИ ДЖЕТА
НЕКОТОРЫЕ ОБОБЩЕНИЯ КОНВЕКТИВНОЙ МОДЕЛИ ГЕНЕРАЦИИ ДЖЕТА
Аннотация
Для аналитического описания начальной стадии генерации джета в неравновесной неоднородной плазме в магнитогидродинамическом приближении проанализированы возможные обобщения решений нелинейного уравнения для функции тока. Модель генерации джета опирается на механизм конвективной неустойчивости и условие вмороженности силовых линий магнитного поля и характеризуется рядом свободных параметров. Уравнение для радиальной части функции тока удовлетворяется функциями Бесселя первого порядка. Чтобы удовлетворить всем условиям вблизи оси джета и на его периферии, найденные решения гладко стыкуются на границе. Итоговое аналитическое решение для поля скорости применимо для произвольных значений безразмерных координат. Полоидальная скорость нарастает примерно по экспоненциальному закону, а азимутальная скорость – по сверхэкспоненциальному закону. В работе рассчитано поле скорости джета, который составлен из семи участков. Вращение джета оказывается дифференциальным, причём для получения решения в квадратурах для азимутальной скорости можно использовать не только линейные, но и степенные зависимости от высоты. При показателе степени n < 1 сразу от оси джета наблюдается заметный рост азимутальной скорости с радиусом, а при n > 1 вблизи оси наблюдается область относительного затишья. Модель джета обобщена на случай произвольной зависимости частоты Брента – Вяйсяля от высоты. Найдены соответствующие решения для радиальной и вертикальной компонент скорости. Для начальной стадии развития в работе также найдены вертикальная и азимутальная компоненты генерируемого магнитного поля джета.
1. Введение
Среди структур в магнитосферной, лабораторной и космической плазме довольно часто наблюдаются направленные струи – джеты , . Подобные локализованные нестационарные объекты представляют собой вытянутые вихревые структуры, в которых наблюдается спиральное движение. При этом скорость движения плазменного выброса и поля достигают максимальных значений в определённой области и убывают на периферии структуры. Наблюдаемый в природе широкий класс джетов включает в себя астрофизические джеты , , , солнечные корональные джеты и петли , , и магнитосферные джеты , , , . Исследование возникающих в плазме динамических структур является одной из фундаментальных задач физики и представляет большой теоретических и практический интерес.
Многочисленные работы посвящены развитию теории плазменных джетов , , , , исследованию их динамики, в том числе учитывающей циклотронное движение вещества, , , , . В связи с явными ограничениями существующих моделей (см., например, , , , ), отыскание новых решений является актуальной задачей. Создание моделей генерации джетов открывает наиболее простой и корректный путь к получению ряда теоретически и практически интересных результатов. В работе построена малопараметрическая магнитогидродинамическая модель описания начальной стадии развития нерелятивистских джетов, основанная на механизме конвективной неустойчивости. Новая аналитическая модель позволяет описывать структуру магнитного поля и скорости локализованного в пространстве джета в приполярных областях при всех значениях координат и представляет собой точное решение в виде комбинаций функций Бесселя.
Целью настоящей работы является обобщение предложенной аналитической модели на случай неоднородной плазмы.
Основной метод исследования – теоретический анализ возникающих в плазме структур в рамках идеальной магнитной гидродинамики. Описание использует понятие функции тока. Основной математический метод получения точных решений – метод разделения переменных. Для приближённых оценок используется метод последовательных приближений. Визуализация решений в виде графиков и численный счёт осуществляется с помощью программы Wolfram Mathematica.
2. Основные результаты
2.1. Основное уравнение для функции тока
В работе
в цилиндрической системе координат (r,φ,z) в осесимметричном случае ∂/∂φ=0 была выписана система уравнений идеальной магнитной гидродинамики (МГД) и рассмотрены слабые возмущения давления, плотности и магнитного поля:где B0=(0,0,Bz); величины p0, ρ0, B0 – равновесные невозмущённые значения, а p ̃, ρ ̃и B ̃– малые возмущения соответствующих величин на начальном этапе развития неустойчивости. В равновесном состоянии
где μ0 – магнитная проницаемость вакуума, g=-gez – гравитационное ускорение на Солнце (звезде, или в магнитосфере планеты), ez – единичный вектор вдоль вертикали. В случае бездивергентного потока v=(vr, vφ, vz) можно ввести функцию тока ψ(t,r,φ,z):
для которой в , из системы МГД-уравнений было получено следующее уравнение:
В данном уравнении введены обозначения для Якобиана
для оператора Грэда–Шафранова (в приближении вытянутых структур ∂/∂r>>∂/∂z):
и для квадрата частоты Брента–Вяйсяля:
где γa – показатель адиабаты, T – температура газа; характерный масштаб высоты . Уравнение (4) применимо к полярным джетам, когда для итогового магнитного поля
. В частности, в работе
В случае ωg2>0 уравнение (4) описывает внутренние гравитационные волны. Мы рассматриваем противоположную ситуацию, когда в момент t = 0 возникает неустойчивость, т.е. в (4) имеем ωg2→-γ2. В этом случае уравнение (4) описывает растущие со временем локализованные динамические структуры. Такая ситуация возникает, если внутренние области плазмы (Солнца, звезды, или магнитосферы) более горячие, чем более высокие слои плазмы: если вертикальный градиент температуры (второй член в (7)) отрицателен, и его величина превышает первый член.
Решение в работе
искалось методом разделения переменных:где Z=z/L, R=r/r0, а v0, r0, L – некоторые характерные скорость, радиальный и вертикальный пространственные масштабы. Для внутренней и внешней области соответственно были выбраны следующие решения:
где δ0≈1.841184, параметр δ произволен, а величина m определяется из условия гладкой стыковки функции и её производных на границе внутренней и внешней области.
Для определения азимутальной скорости в
использовалось уравнение:Оно допускает решение методом разделения переменных
если выбрать линейную функцию f(Z). В таком случае получаем
а координатная зависимость определяется уравнением
В работе
была выбрана линейная функция f0(Z)=f(Z) с максимумом при Z = L/2. Тогда радиальная зависимость выражается в квадратурах. Полученные соответствующие графики для составляющих поля скорости можно посмотреть в работе . Для удобства сравнения мы будем использовать в данной статье такие же свободные параметры модели.2.2. Некоторые обобщения модели джета
Для срабатывания метода разделения переменных можно выбрать следующее более общее линейное выражение для функции
где Z1 определяет координату максимума, а k1 определяет скорость изменения с высотой. При этом наиболее общим выражением для функции f0(Z), которое допускает радиальное решение в квадратурах, будет следующее:
с произвольным показателем степени n. В результате будет наблюдаться различное дифференциальное вращение. Азимутальная скорость определяется квадратурами:
Полученную радиальную зависимость легко рассчитать численно (мы взяли α = 0,01) и изобразить графически с помощью программы Wolfram Mathematica (функция Plot). При n < 1 быстрое возрастание азимутальной скорости по радиусу начинается сразу от оси джета, как это видно из Рис. 1, а при n > 1 мы видим вращение полого цилиндра (см. Рис. 2), т.е. вблизи оси наблюдается область относительного затишья.
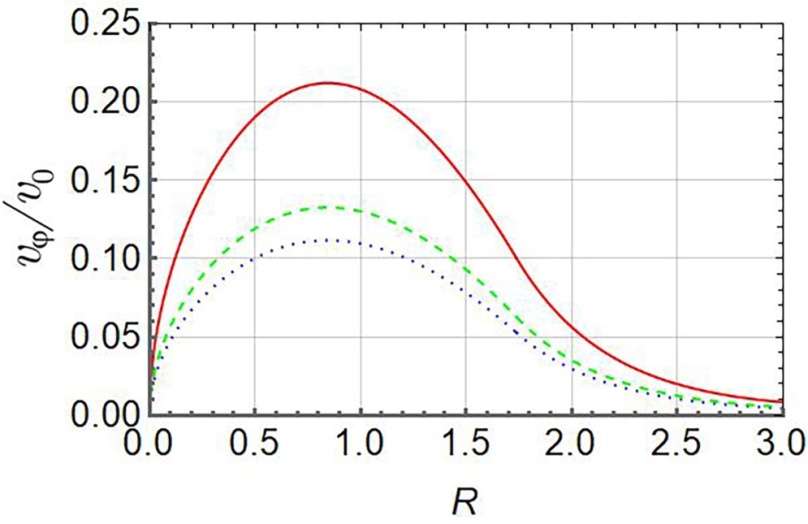
Рисунок 1 - Радиальная зависимость относительной азимутальной скорости vφ/v0 при z/L=0,1 и n = 0,75:
пунктирная линия - момент времени γt = 3; штриховая - γt = 4; сплошная - γt = 5
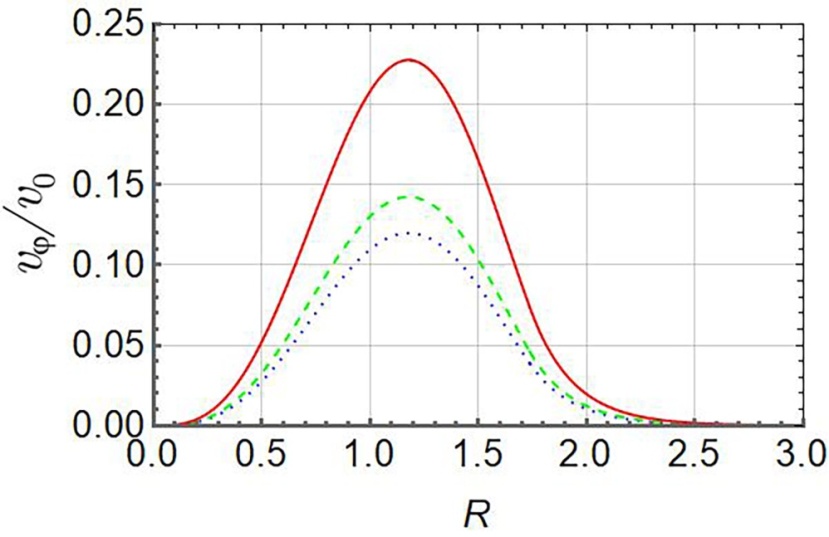
Рисунок 2 - Радиальная зависимость относительной азимутальной скорости vφ/v0 при z/L=0,1 и n = 2:
пунктирная линия - момент времени γt = 3; штриховая - γt = 4; сплошная - γt = 5
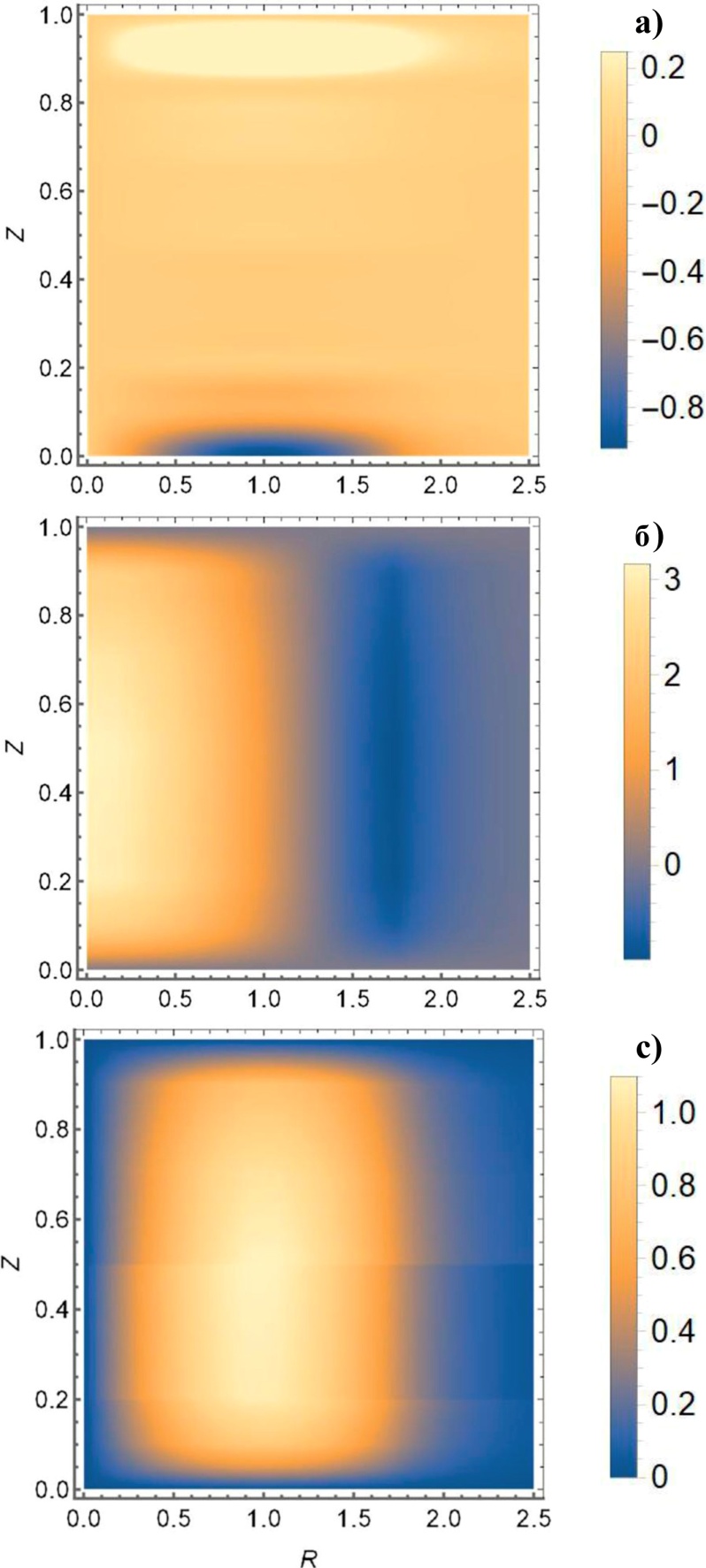
Рисунок 3 - Поле скоростей джета, который сконструирован по высоте с помощью семи линейных участков функции f(Z), в зависимости от безразмерных координат R и Z:
a - vr(R,Z); б - vz(R,Z); c - vφ(R,Z)
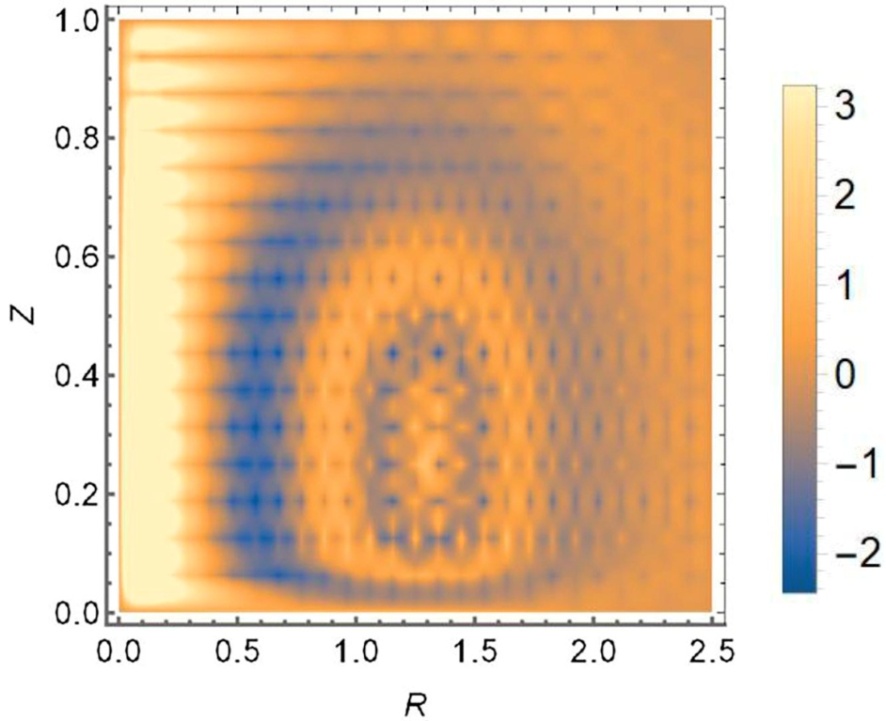
Рисунок 4 - Пример разнонаправленной азимутальной скорости джета vφ(R,Z), зависящей от безразмерных координат R и Z, для случая нелинейной зависимости f(Z)
Для реальной системы частота Брента – Вяйсяля всегда зависит от высоты. Заметим следующий важный момент, связанный со структурой уравнения (4). При произвольной z-зависимости частоты Брента – Вяйсяля ωg(z) решением останется та же самая функция тока ψ. Дело в том, что последнее слагаемое в (4) удовлетворяется только за счёт радиальной зависимости, а первое слагаемое удовлетворяется только за счёт зависимости от времени. Таким образом, в выражении для функции тока произойдёт единственная замена: γ→γ(Z), т.е. скорость роста всех величин будет дифференциальной по z. В результате, в выражении для вертикальной компоненты скорости произойдёт единственная замена: γ→γ(Z). Однако в выражении для радиальной компоненты скорости кроме замены γ→γ(Z) также произойдёт следующая замена: f'(Z)→f'(Z)+f(Z)γ'(Z)tCoth[γ(Z)t]. Как следствие, уравнение (11) уже нельзя решить методом разделения переменных, и зависимость от всех трёх переменных нужно искать численно.
Генерируемое магнитное поле можно найти из следующего уравнения (условия вмороженности магнитного поля в плазму):
На начальном этапе генерации итоговое поле можно найти методом последовательных приближений:
где уравнения для соответствующих поправок имеют следующий вид:
при этом начиная со вторых поправок возможен только численный счёт, а для первых поправок решения можно записать в квадратурах:
Генерируемая вертикальная компонента магнитного поля начинает экспоненциально расти по модулю, (затем рост постепенно перейдёт в сверх экспоненциальный). Азимутальная компонента магнитного поля растёт по сверхэкспоненциальному закону, но вначале медленнее, чем вертикальная компонента. Радиальная компонента магнитнго поля растёт ещё медленнее и всегда остаётся меньшей из этих трёх компонент поля. Для случая семи линейных участков функции f(Z) распределение итоговой вертикальной компоненты и азимутальной компоненты магнитного поля показаны на Рис. 5 а) и б) соответственно. Графическое изображение получено с помощью программы Wolfram Mathematica (функция DensityPlot).
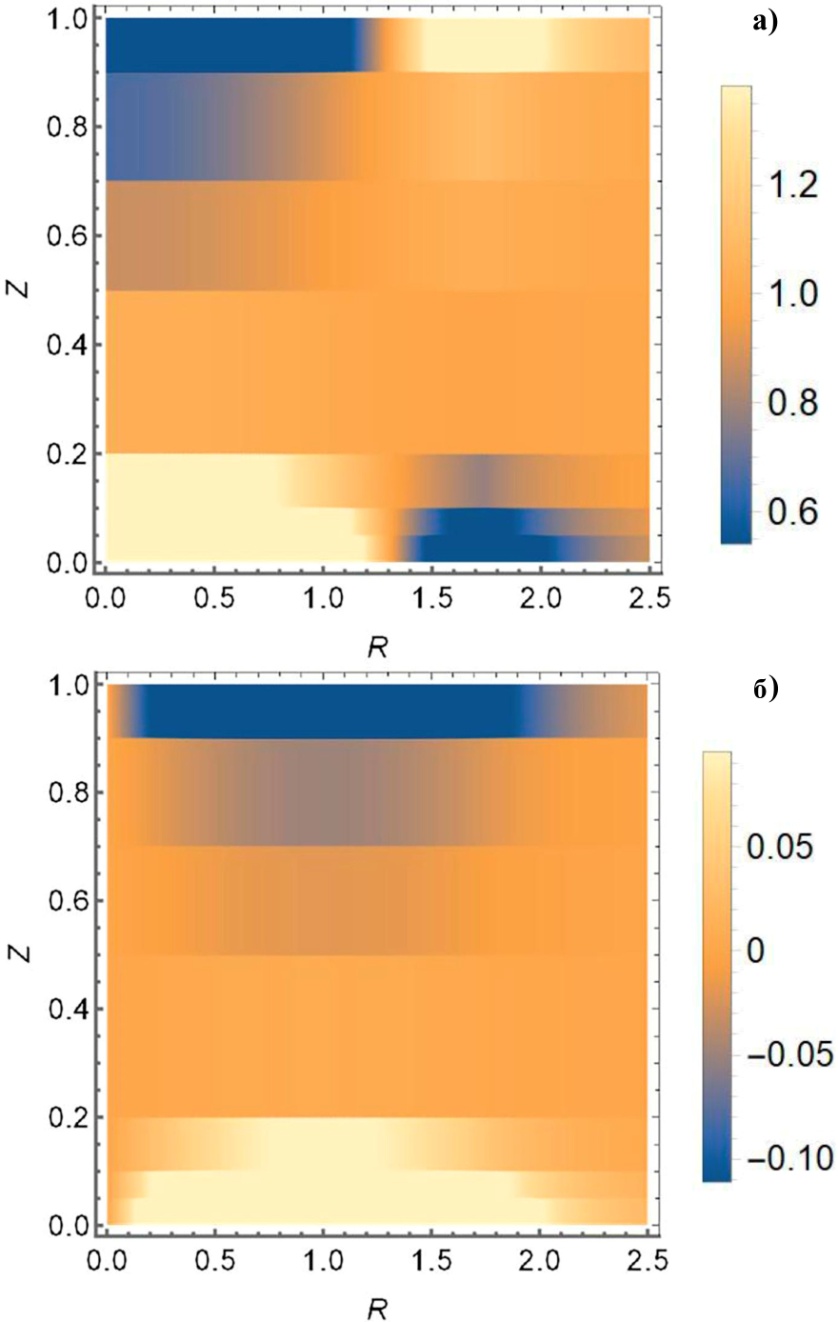
Рисунок 5 - Итоговое безразмерное магнитное поле на начальном этапе роста в зависимости от безразмерных координат R и Z:
a - Bz(R,Z)/B0; б - Bφ(R,Z)/B0
Примечание: джет сконструирован по высоте с помощью семи линейных участков функции f(Z)
3. Заключение
В настоящей работе в рамках идеальной МГД приведено нелинейное уравнение для функции тока, которое в неустойчивой стратифицированной плазме описывает образование аксиально-симметричных структур, растущих во времени. Полученное уравнение можно решить методом разделения переменных, что позволяет для радиальной части получить в качестве решений функции Бесселя первого порядка. Для удовлетворения всем условиям вблизи оси джета и на его периферии, найденные решения гладко стыкуются в промежуточной области. В результате получается аналитическое решение для поля скорости применимое для всех значений безразмерных координат R и Z. Модель джета характеризуется рядом свободных параметров: характерной радиальной скоростью v0 и начальной азимутальной скоростью v0φ; характерным радиальным масштабом джета r0 и вертикальным масштабом L; параметром m, который характеризует радиальную структуру джета; однородным внешним магнитным полем B0 и инкрементом конвективной неустойчивости γ. Джет может быть сконструирован по вертикали из ряда участков. В данной работе рассчитано поле скорости для джета, который составлен из семи линейных участков. Полоидальная скорость нарастает примерно по экспоненциальному закону, а азимутальная скорость – по сверхэкспоненциальному закону. Вращение джета оказывается дифференциальным, причём для получения решения в квадратурах для азимутальной скорости можно использовать не только линейные, но и степенные зависимости по высоте Zn. При n < 1 быстрое возрастание азимутальной скорости по радиусу начинается сразу от оси джета, а при n > 1 вблизи оси наблюдается область относительного затишья. Модель джета обобщена на случай произвольной z-зависимости частоты Брента – Вяйсяля ωg(z). Найдены соответствующие решения для радиальной и вертикальной компонент скорости. В случае произвольной зависимости от высоты уравнение для азимутальной скорости нельзя решить методом разделения переменных, и зависимость от всех трёх переменных нужно искать численно. В этом случае могут получаться решения с разнонаправленными вращениями. Для начальной стадии развития в работе также найдены вертикальная и азимутальная компоненты генерируемого магнитного поля джета, который составлен из семи линейных участков.
Таким образом, в конвективно-неустойчивой плазме чрезвычайно быстро формируются интенсивные джеты. Обобщённая модель описывает генерацию поля скорости и магнитного поля, величина которых нарастает со временем.
