Modelling and optimization of additive systems based on intelligent decision-making support

При аддитивных технологиях создание объектов осуществляется путем последовательного формирования один слой за другим. Существуют классификации аддитивных технологий относительно материалов, которые используются, по источникам и методам подвода энергии. Разные варианты технологий определяют соответствующую совокупность дефектов получаемых объектов.

Например, прямое лазерное выращивание осуществляется при помощи того, что отдельные дорожки наносятся последовательным способом. Существует неоднородность в пространственных распределениях потоков порошков и лазерном излучении. Например, профиль сначала сходится, а затем расходится.

В этой связи есть необходимость в оптимизации технологических параметров лазерного выращивания.

В ходе моделирования возникают возможности для уменьшения веса деталей, для осуществления топологической оптимизации, для обеспечения внутренних воздушных каналов.

В связи с тем, что скорости охлаждения являются достаточно большими, в деталях будет наблюдаться возникновение мелкозернистых структур. Чтобы предотвращать появление микроразрушений, необходимо понимать, каким образом будет строиться вся конструкция, где будет прогнозироваться наименьшее сопротивление. Алгоритмы такого поиска приводятся в этой работе.

Подходы к внедрению аддитивных технологий в процессы производственных предприятий требуют дополнительного анализа. Прежде всего, к таким вопросам относятся аспекты интеграции аддитивных технологий в бизнес-архитектуру и архитектуру информационных систем предприятия. Для внедрения аддитивного производства требуется комплексный подход, затрагивающий различные аспекты управления предприятием. Фактор сложности влияния технологии аддитивного производства на предприятия в целом обуславливает необходимость разработки проектного подхода к их внедрению. 

В работе представлена модель модернизации технологического процесса аддитивного производства на основе технологий промышленного интернета вещей, аппаратной реализацией которого является одноплатный компьютер Raspberry Pi, программной реализацией является MTConnect – промышленный стандарт обмена данными станков с числовым программным управлением. Использование Raspberry Pi, подключенных к нему датчиков и программного обеспечения OctoPrint реализует контроль и удаленное управление технологическим оборудованием аддитивного производства (3D-принтером) в режиме реального времени.

Изменение подхода к организации аддитивного производства в рамках таких концепций, как Industry 4.0, Smart Manufacturing, Manufacturing Cloud, Society 5.0 заключается в создании виртуальной модели производственной системы, прогнозирующей поведение реального объекта с высокой степенью точности.

Происходят изменения подходов к управлению глобальными цепочками стоимости в процессе разворачивающейся новой промышленной революции в части такого ее компонента, как аддитивное производство или 3D-принтинг.

Анализ современных литературных источников показывает, что аддитивное производство характеризуется большим числом неопределенных параметров, что требует использования интеллектуальных подходов в управлении.

Целью работы является разработка подхода, позволяющего осуществлять моделирование и оптимизацию аддитивных процессов на основе интеллектуальной поддержки принятия решений.

Проведем рассмотрение адаптивного подхода, когда формируется аддитивная структуры. При этом будут определяться параметров модели агрегирования параметров тех объектов, которые в нее входят. При этом необходима процедура имитационного эксперимента.

В имитационном эксперименте применяется вычислительная процедура создания последовательностей анализируемых компонентов. При этом применяется информация о значениях рассматриваемых показателей 

Необходимо сформировать данные, чтобы был реализован эксперимент. Они будут следующими.

1. Происходит согласование со стороны экспертов обучающего нумерационного множества уровней прочности материалов (

2. Значения показателей, которые входят в обучающую выборку, будут подготовлены 

3. Важно указать набор альтернативных вариантов для моделей интегрального оценивания 

4. Показателей определяются тремя способами 

Первый связан с обучающей выборкой. По каждому из показателей формируем множество уровней прочности 

где преобразующая функция – это 

Линейное преобразование искомых показателей используется для их нормирования. Применяется безразмерная шкала [O, А]. Проводится расчет прочности. При этом рассматривается максимальные 

При помощи статистических характеристик ведется нормировка показателей. Тогда оцениваются математические ожидания 

Для каждого альтернативного варианта определяются номера уровней прочности. При этом используем обучающую выборку. Рассматриваются заданные значения 

Вводится критерий оптимизации. В ходе рассмотрения интегрального оценивания выбирается его соответствующая структура, а также характеристики моделей. Критерий оптимизации рассматривается в виде расстояния Хемминга. Проводится его оценка с точки зрения того, какой номер в размещении объекта, который относится к обучающей выборке 

В представленном выражении расстояния Хемминга – это 

В функции (1) происходит определение варианта структуры. Для критерия (3) проводится рассмотрение способа нормирования. Происходит это при полном переборе по всем сочетаниям 

Почему выбирается рандомизированная схема? На это влияет неопределенный характер поведения ступенчатой целевой функции (4). За счет нее параметры вектора 

В рассматриваемой ситуации в k-й (k=1,2,...) точке каждый параметр при итерационном поиске 

в указанном выражении 

При этом шаги 

значения плотности распределения 

где 

Требуется выполнение условия 

Наблюдается завершение поиска, когда k будет равно K.

На рисунке 1 приведена схема идентификации адаптивной структуры.

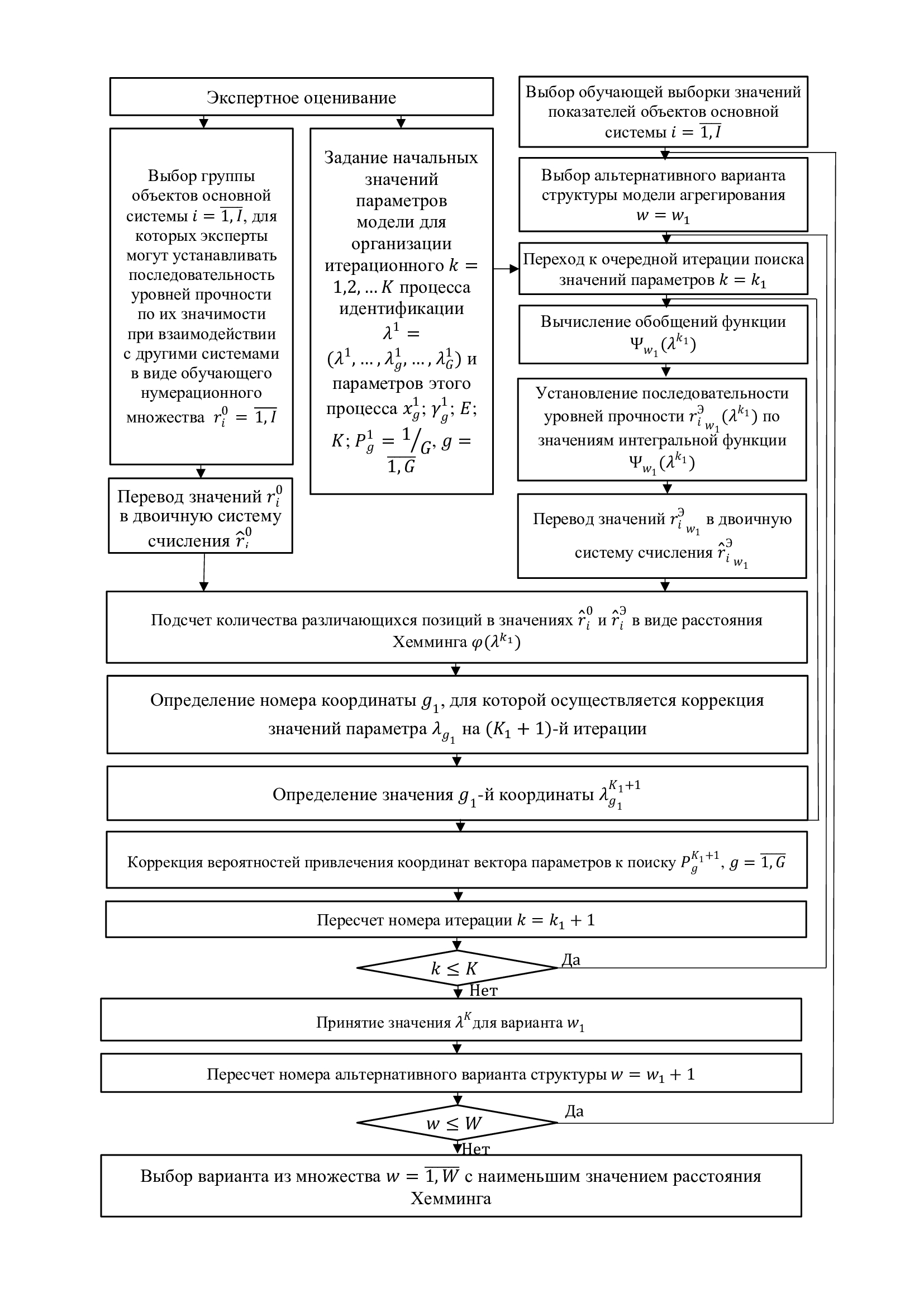
Рисунок 1 - Схема идентификации адаптивной структуры

DOI:10.60797/IRJ.2024.148.24.1

Основными компонентами являются алгоритма поддержки принятия решений:

1. Проведение создания оптимизационной модели.

2. Осуществление выделения уровней 

3. Проведение интеграции вероятностной интерпретации прочности и процедуры решения оптимизационной задачи на базе рандомизированного поиска.

4. Создание множества доминирующих вариантов совокупности тех показателей, которые наибольшим образом будут оказывать влияние 

Оптимизационная модель создается, когда применяются булевые переменные. Они подвергаются оптимизации

Задача состоит в минимизации числа показателей. Они входят в набор 

Можно говорить о том, что формируется соответствующее условие, которое связано с тем, что для любого анализируемому типа из материалов в число показателей, которые влияют, будет входить не менее, чем один показатель

В указанном выражении 

Проводим объединение критерия оптимизации (10), ограничений (11) и требования относительно оптимизируемых переменных (9). Тогда получается оптимизационную модель:

Виды материалов 

Исходя из того, что значения (13) влияют на характеристики эффективности в поиске [ ] происходит интеграция их в случайную схему. При этом определяются вероятностные параметры по k=2,3,... итерациям

Здесь 

Как результат по заданному числу итераций K можно получить множество при значениях 

Экспертное ранжирование применяется для того, чтобы осуществлять окончательным образом выбор варианта. Помимо этого, происходит определение варианта, относящегося к наименьшей прочности материала. Для значений 

Проведение обработки результатов топологической оптимизации первичным образом было осуществлено в ANSYS SpaceClaim. Получена фасеточная модель конструкции. После этого проводили ее ручное редактирование. При этом необходимо было удалять полости, углубления, тонкие тоннели. Проводилось сглаживание модели и преобразование в твердотельную геометрическую модель. Этот процесс реализовывался при помощи того, что накладывались NURBS поверхностей к каркасной модели. Необходимо было использовать программу Geomagic Studio.

На основе Geomagic Studio есть возможности для того, чтобы полным образом автоматически вести формирование NURBS поверхностей. Ту CAD модель, которую мы получили, доработали при помощи системы Solid Works. При этом учитывались технологические ограничения. Это определялось за счет того, что удалялись области с дефектами. Помимо этого осуществлялся процесс добавления областей при построении на основе граничных профилей и траекторий.

Происходила реализация процедур восстановления необходимой симметрии конструкции, было осуществлено преобразование ребер жесткости, были организованы места креплений компонентов конструкции, в согласовании с ответными частями соединяемых тел. Осуществлено добавление необходимых конструктивных компонентов кронштейнов – крепежные отверстия, площадки и произведены необходимые скругления. Та CAD-модель, которая была сформирована, применялась для поверочных расчетов напряженно-деформированного состояния внутри системы ANSYS Workbench.

Среди важных параметров в ходе реализации печати мы можем отметить: диаметр сопла печатающей головки и высота слоя, определяющиеся из геометрических параметров модели и необходимой точности изготовления, скорость и температура экструзии, в основном определяющиеся материалом и требованиям по качеству печати.

С учетом того, какие наименьшие размеры внутри кронштейна мы осуществили выбор сопла, которое характеризовалось диаметром 0,45 мм. Для него качество в ходе реализации печати будет наилучшим, когда наблюдается высота слоя в 0,08 мм. Чтобы осуществлять повышение адгезии, применяли подогрев печатного стола до 135 C. При этом значение температуры экструдера печатающей головки мы создавали 325 C. Значение максимальной скорости движения печатающей головки при печати – 3450 мм/мин.

Стоит отметить, что фактическая скорость может отличаться от максимальной в меньшую сторону на участках, требующих большее количество времени на остывание слоя, чем время печати слоя на максимальной скорости. Данный параметр в Simplify 3D контролируется автоматическим образом.

Таким образом, на основе алгоритма идентификации структуры и параметров агрегационной модели аддитивных систем осуществляется оптимизация объекта, создаваемого при аддитивном производстве. Приведена схема идентификации адаптивной структуры. Рассмотрены алгоритмы интеллектуальной поддержки принятия решений при формировании структуры объекта. Применялось экспертное ранжирование в ходе окончательного выбора варианта аддитивной структуры. Результаты подтвердили возможность использования предлагаемых алгоритмов на практике.