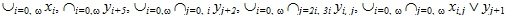СЛОЖНОСТЬ ВЫЧИСЛЕНИЯ ПРОГРАММ

Попов С.В.

Кандидат физ.-мат. наук, Колледж автоматизации и информационных технологий №20, Москва

СЛОЖНОСТЬ ВЫЧИСЛЕНИЯ ПРОГРАММ

Аннотация

Описывается сложность вычисления программ в зависимости от вида вычисляемых ими функций.

Ключевые слова: арифметические программы, сложность вычисления, обобщенный пропозициональный язык.

Popov S.V.

Candidate of ph.-m. sciences, College of automation and information technologies №20, Moscow

DEVELOPMENT AND IMPLEMENTATION OF THE METAL DETERGENT PRODUCTION PROJECT

Abstract

Complexity of calculation of programs depending on a type of functions calculated by them is described..

Keywords: arithmetic programs, complexity of the calculation, generalized пропозициональный language.

Обобщенный пропозициональный язык

Пропозициональный язык представляет собой удобное средство для описания широкого спектра содержательных задач [2]. С другой стороны, его выразительных возможностей не хватает для описания задач, связанных с вычислительными моделями. Поэтому расширение пропозиционального языка привело к появлению новых языков: модальные, динамические логики и бесконечные пропозициональные языки. Изучение разнообразных расширений пропозиционального языка представляет интерес как своими теоретическими, так и прикладными аспектами.

В работе рассматривается расширение пропозиционального языка путем введения бесконечных логических связок. Если не ограничивать эти связки, то в результате получается язык, в котором представимы все вычислимые функции. Исследование такого языка сопряжено с определенными трудностями. Чтобы их избежать предлагается рассмотреть так называемый примитивный пропозициональный язык, полученный путем введения определенных ограничений на бесконечные связки. В некотором отношении он трактуется как обобщение модальных языков.

Основная цель построения обобщенного языка состоит в использовании его для анализа вычислительных программ и переписывающих алгоритмов. В итоге удается выделить ряд свойств программ, позволяющих делать выводы о вычисляемых ими функциях при ограничениях на сложность вычислений.

Расширение булевского языка над базисом {∨, ∧, ¬} осуществляется путем обобщений дизъюнкции и конъюнкции на не более, чем счетное множество аргументов. Для обобщенных дизъюнкции и конъюнкции используются выражения соответственно ∪_{i=k, h} и ∩_{i=k, h}, где i называется индексом этой связки, k – нижней границей, а h – верхней. k и h – это либо константы, либо символ бесконечности, либо целочисленные функции, зависящие от других индексов.

Введем определение формулы в расширенном базисе.

1. Полагаем, что задано счетное множество переменных x, y, z, … , возможно с индексами, каждая из которых есть формула. Одна переменная может обладать несколькими индексами.
2. Если A, A₁ – формулы, то A ∨ A₁, A ∧ A₁ и 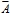 суть формулы.
3. Если h, k – нижняя и верхняя границы, f_i, i = k, k+1, k+2, …, h – суть формулы, то ∪_{i=k, h} f_i и ∩_{i=k, h} f_i также суть формулы. Будем говорить, что все формулы f_i находятся в области действия связок соответственно ∪_{i=k, h} и ∩_{i=k, h}. Это же относится к каждой их подформуле. Если f_i содержит в качестве подформулы обобщенную формулу, то ее границы могут быть либо константой, либо символом бесконечности, либо значением некоторой целочисленной функции от i и других индексов (эти функции назовем граничными).

Пример 0.1. Следующие выражения суть формулы:

Укажем несколько возможных семантик обобщенных формул.

• Временная семантика с дискретным временем.
• Семантика линейного порядка с определенными ограничениями, которые задаются обобщенными формулами.
• Семантика в виде вычислимых функций, когда все переменные одного типа с различными индексами, например, x₀, x₁, x₂, … трактуются как компоненты бинарного вектора x₀x₁x₂ … , представляющего двоичную запись числа.

В последующем вводятся ограничения на индексы обобщенных связок, позволяющие выделить подмножество обобщенных формул, – т.н. примитивный язык. Последний обладает хорошими выразительными возможностями, и легко поддается исследованию.

Наиболее важная для нас семантика обобщенных формул связана с представлением вычислимых функций, когда обобщенная формула является характеристической для вычислимой функции. В частности, обобщенная формула F(x₁, x₂, …, x_n, y) представляет двоичную функцию y = f(x₁, x₂, …, x_n), если при означивании переменных x₁, x₂, …, x_n, y соответственно бинарными векторами σ₁, σ₂, …, σ_n, σ_n+1 формула F(σ₁, σ₂, …, σ_n, σ_n+1) истинна тогда и только тогда, когда f(σ₁, σ₂, …, σ_n) = σ_n+1. Оказывается, что обобщенный язык с введенными ограничениями на индексы переменных, позволяет представлять все функции арифметики Пресбургера.

Для примитивного языка существенно свойство локальности его формул. Содержательно, его можно сформулировать так. Если F(x) есть локальная формула, то при всяком начальном означивании переменной x получается лишь конечное число не эквивалентных формул, число которых определяется только видом формулы F(x) и не зависит от длины начального означивания. Из этого вытекает, что всякая функция, которая представима примитивной формулой, вычислима за линейное время. А так как все функции арифметики Пресбургера представимы примитивными формулами, то они также вычислимы за линейное время.

Сложность вычисления арифметических программ

В этой части работы исследуются свойства программ над двоичным арифметическим базисом [1]. В качестве базисных операторов в программах используются операторы присваивания, оператор проверки равенства/неравенства и арифметические операторы – обнуление переменной и прибавления единицы. Известно, что этот базис полный, т.е. для любой рекурсивной функции существует вычисляющая ее программа.

Так как рассматриваются двоичные функции, то каждая переменная x представляется в виде бесконечного набора булевских компонентов: x₀x₁x₂… x_i … . При этом слабые разряды располагаются слева. Тогда каждое двоичное число представляется двоичным префиксом, оканчивающимся единицей, после которого следует бесконечный нулевой суффикс. Например, бесконечная последовательность 10100… 000 … обозначает число 5.

Вводится понятие начального означивания переменной, когда ее конечный префикс, оканчивающийся единицей, представляет двоичное число, после которого располагаются неозначенные переменные. Например, таким означиванием может быть 101x₃x₄… x_i … . Основываясь на частичном означивании двоичной переменной, вводится понятие функции, определенной начальным означиванием ее аргумента. Для простоты приведем это определение на примере функции с одним аргументом. Пусть φ(x) есть двоичная функция, где x рассматривается как бесконечный набор двоичных компонентов, и σ_x есть начальное означивание аргумента. При таком означивании функция φ(x) преобразуется в функцию  φ(x)|_σx значения которой определяются оставшимися не означенными компонентами аргумента x. При этом мы игнорируем т.н. неподвижные компоненты значения функции j(x), т.е. компоненты, которые не меняются при расширении означивания σ_x. Два начальных означивания σ'_x и σ"_x эквивалентны, если они определяют одну функцию.

Тем самым при различных начальных означиваниях σ_x вводится семейство функций φ(x)|_σx, порождаемых различными начальными означиваниями. И мощность фактор-множества введенной эквивалентности частичных означиваний служит характеристикой сложности исходной функции. Это напоминает бинарные программы для логических функций, когда сечение программы рассматривается как мера сложности логической функции.

Здесь мы решаем задачу описания сложности программ, вычисляющих арифметические функции в зависимости от мощности их фактор-множеств. Инструментом исследования выступает обобщенный пропозициональный язык, формулы которого строятся над базисом, расширенным за счет введения бесконечных логических операций. Обобщенные пропозициональные формулы представляют арифметические и логические операторы, которые образуют полный базис для рассматриваемых арифметических программ. Поэтому средств обобщенного языка достаточно для представления программ, вычисляющих все арифметические функции.  Представление программы, в общем случае, порождает формулу не ограниченной длины. Тем самым обобщенный язык полон, т.е. обладает возможностью представлять все вычислимые арифметические функции.

По аналогии с частичным означиванием аргумента функции определяется вычисление программы для частично означенного входа, что естественно приводит к возникновению неопределенности продолжения вычисления программы. Однако, число элементарных вычислений программы до возникновения неопределенности определяется мощностью фактор-множества. В частности, основной результат этого раздела выглядит так: для арифметических программ длина вычисления не меньше величины h^c, где h – это мощность фактор множества эквивалентности частичных означиваний входа, а c – константа, определяемая видом программы и количеством ее рабочих переменных.

Литература

1. Янов Ю.И. О вычислениях в одном классе программ // Проблемы кибернетики. – 1977. №32.– С. 200-230.
2. Попов С.В., Брошкова Н.Л. Прикладная логика. – М.: Физматлит, 2011. – 212 с.