МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ ПЕРЕХОДНОГО ПРОЦЕССА НАПРЯЖЕНИЯ СИНХРОННОГО ГЕНЕРАТОРА
МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ ПЕРЕХОДНОГО ПРОЦЕССА НАПРЯЖЕНИЯ СИНХРОННОГО ГЕНЕРАТОРА
Аннотация
Исследуется переходный процесс синхронного генератора, возникающий при изменении внешнего эквивалентного индуктивного сопротивления. В рассматриваемом переходном процессе отклонение напряжения на шинах генератора остается в рамках допустимого для нормального режима. Производится оптимизация с векторным критерием качества (многокритериальная оптимизация) переходного процесса напряжения на шинах генератора путем изменения ЭДС возбуждения, т.е. задача синтеза оптимального закона управления возбуждением генератора в виде кусочно-линейной функции с заданными узлами интерполяции по времени. Выполнено построение с помощью генетического алгоритма в пространстве критериев множеств Парето и их последующее сужение в соответствии с аксиоматическим подходом.
1. Введение
Задача оптимизации переходного процесса синхронного генератора с помощью надежных, быстродействующих, совершенных алгоритмов управления его возбуждения является по-прежнему актуальной. Не прекращается появление новых публикаций на тему методов оптимизации различными метаэвристическими алгоритмами настроек ПИД-регулятора возбуждения синхронной машины и его разновидностей (ПИД-регулятор дробного порядка, с производной второго порядка и др.)
, , , . Однако стратегии, основанные на ПИД-регулировании, будут являться более предпочтительными (из-за меньшего количества вычислительных операций) только в случае оптимальной настройки коэффициентов регулятора .Параметры ПИД-регулятора возбуждения, выбранные с помощью какой-либо оптимизационной процедуры, могут быть постоянными и(или) непрерывно изменяющимися, подстраиваемыми в соответствии с режимом ЭЭС в адаптивных и интеллектуальных схемах управления
, , .Оптимальный переходный процесс здесь и далее понимается нами как наилучший в смысле одного или нескольких критериев эффективности переходный процесс в условиях определенного возмущения — нормального эксплуатационного режима или аварийного режима. Традиционно для оптимизации переходного процесса синхронного генератора выбирают какой-либо из критериев: скорость затухания, размах колебаний, скорость регулирования напряжения при изменении уставки; скорость восстановления напряжения к заданному значению при возмущении со стороны энергосистемы; интенсивность подавления электромеханических колебаний, повышение запаса устойчивости; сам факт обеспечения устойчивости во всех возможных режимах эксплуатации; повышение уровня динамической устойчивости при близких коротких замыканиях и т.д.
Известна неоднозначность выбора целевых функций, являющаяся следствием противоречивости критериев, то есть улучшение одного критерия может приводить к ухудшению другого. Таковы, например, пары: колебательная устойчивость и коэффициент усиления; быстрота демпфирования колебаний и размах колебаний переходного процесса. Таким образом, выбор одного критерия не дает однозначного повышения качества переходного процесса. Это приводит к необходимости искать наиболее эффективное управление переходными процессами, формирования векторного критерия оптимальности, опираясь на известные успехи использования методов многокритериальной оптимизации в решении самых разнообразных технических задач
, , , .Дальнейшая работа с векторным критерием разделяется на два основных направления: использование различных приемов его скаляризации
, (метод главного критерия и сведение остальных к критериальным ограничениям (неравенствам), метод штрафных функций; формирование минимаксного целевого функционала; линейная свертка критериев в один на основе весовых коэффициентов) и построение в пространстве критериев множества Парето с его последующим сужением. В настоящей работе используется второй подход, при этом для построения множества Парето используется генетический алгоритм (ГА).Целью работы является изучение возможностей использования многоцелевой оптимизации для синтеза наилучших законов управления.
В данной работе производится многокритериальная оптимизация переходного процесса напряжения на шинах синхронного генератора в нормальном эксплуатационном режиме. Конкретно рассматривается процесс, вызванный работой синхронного компенсатора: изменение реактивного сопротивления в цепи синхронный генератор — трансформатор — линия электропередачи. Рассмотрено 12 различных критериев качества переходных процессов, объединенных во взаимно противоречащие пары или тройки, для которых выполнено построение множества Парето с учетом технических ограничений. Задача поиска наилучшего переходного процесса рассматривается далее, как задача синтеза оптимального закона управления возбуждением генератора. Результаты проведенных расчетов сравнивались с результатами эталона, в качестве которого принят результат одноцелевой оптимизации с применением одного из традиционных интегральных критериев качества переходных процессов. Проведенное исследование может рассматриваться как первый шаг решения задачи оптимальной настройки коэффициентов усиления АРВ по векторным критериям качества.
Классификации современных направлений развития систем автоматического регулирования возбуждения синхронных генераторов, данная в
, предлагает 4 типа задач:1 — модернизацию существующих линейных структур АРВ;
2 — разработку адаптивных АРВ;
3 — разработку методик по настройке АРВ;
4 — определение оптимальных мест установки АРВ.
Настоящее исследование относится ко второму и третьему типам задач: предварительные шаги для разработки адаптивного АРВ с сохранением существующей линейной структуры ПИД-регулятора или методики по настройке АРВ с элементами адаптивности.
Расчеты проводились на персональном компьютере с процессором уровня i7 10-го поколения в однопоточном режиме.
2. Исходные данные и математическая модель
Переходный процесс в синхронной машина описывается уравнениями Парка-Горева, разрешенными относительно производных:
где eq — ЭДС, обусловленная токами обмотки возбуждения, uв — напряжение на зажимах обмотки возбуждения, ud, uq — поперечное и продольное напряжения статора,
Коэффициенты отражают взаимосвязь электрических параметров синхронного генератора и учитывают примыкающую энергосистему:
где
Дифференциальные уравнения решались методом Дорманда-Принца (разновидность явного метода Рунге-Кутты 4 порядка) средствами MatLab.
3. Решение задачи оптимизации
Предполагается, что изначально генератор работал в нормальном эксплуатационном режиме, а в переходном процессе отклонение напряжения на шинах генератора остается в рамках допустимого для нормального режима (±10%). Задача состоит в подавлении переходного процесса для напряжений на шинах генератора путем изменения ЭДС возбуждения, т.е. задача синтеза оптимального закона управления возбуждением генератора.
Закон изменения возбуждения представлен в виде кусочно-линейной функции с заданными узлами интерполяции
Как уже отмечалось, в настоящей работе основное внимание уделено многокритериальной оптимизации или оптимизации с векторным критерием качества. Векторный критерий представляет собой вектор скалярных критериев, причем желательной является попарная противоречивость входящих в него скалярных критериев. В настоящей работе рассматривались двух- или трехкритериальные постановки, что соответствует одно-, двух- или трехкритериальной оптимизации. Рассматривалась также традиционная однокритериальная оптимизация с нелинейными ограничениями на решения, используемая в работе в качестве некоторого эталона, который желательно улучшить переходом к многокритериальным задачам.
Используемые в работе скалярные критерии качества переходных процессов представлены графически на рис. 1, где смысл критериев интуитивно понятен. Ккритерии промаркированы буквами латинского алфавита и цифрой (если необходимо). Такая маркировка критериев будет использоваться и далее при формировании векторных критериев. Так, векторный критерий, обозначаемый авс1, соответствует трехкритериальной задаче, в которой используются 3 скалярных критерия а, в и с1.
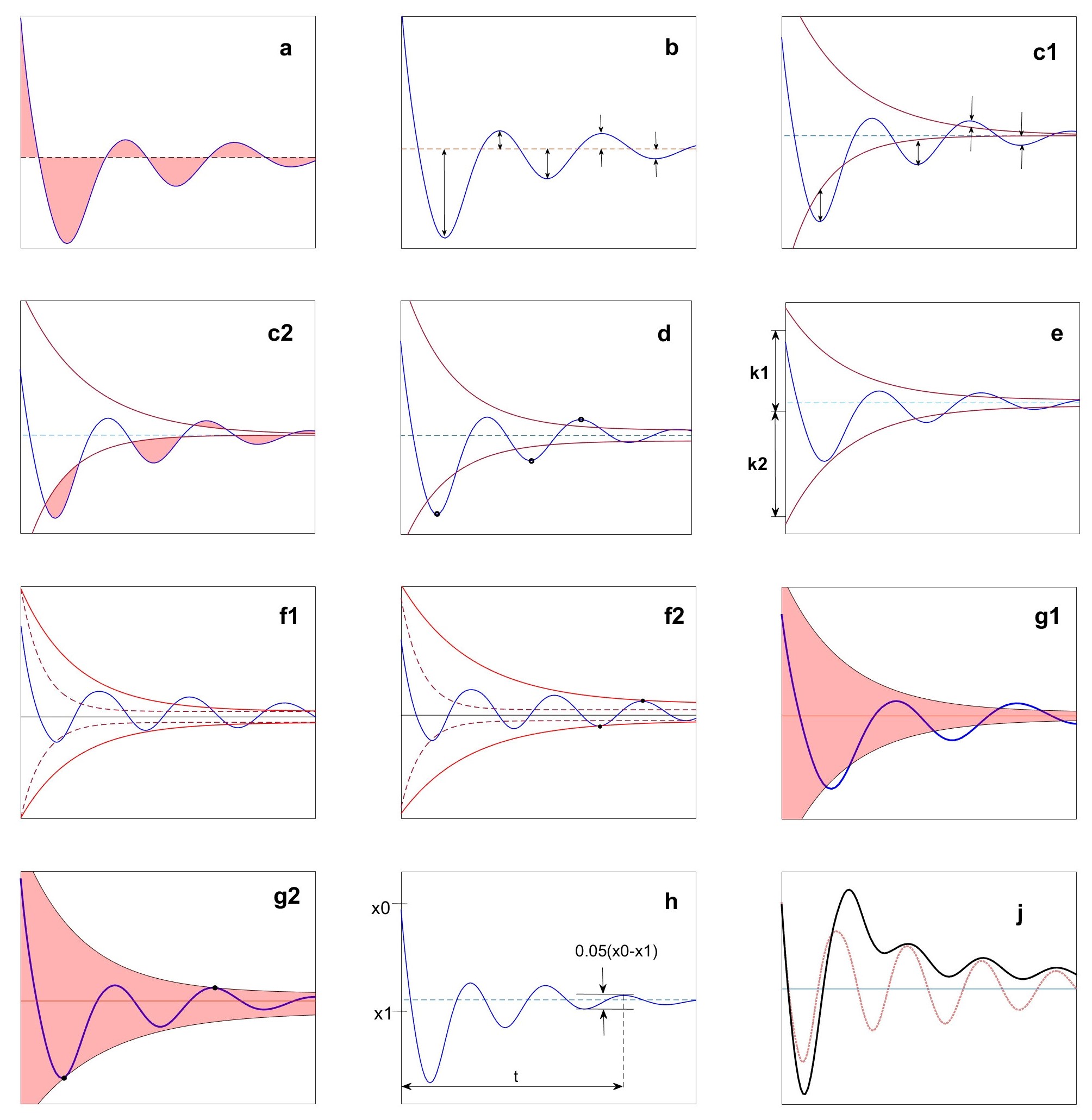
Рисунок 1 - Графическое представление показателей качества переходных процессов
a. Интегральный показатель ошибки, при этом под ошибкой понимается отклонение текущего значения управляемой величины (напряжения генератора) от ее установившегося значения (новое значение напряжения генератора после изменения нагрузки):
b. Сумма модулей отклонений значений экстремумов кривой переходного процесса
c1. Сумма отклонений экстремумов кривой переходного процесса за пределы ограничивающих экспонент
где
k = 0,1,
c2. Интеграл отклонений кривой переходного процесса
k = 0,1,
d. Количество экстремумов кривой переходного процесса
где k = 0,1,
e. Максимальный из предэкспоненциальных множителей
f1. Коэффициенты
f2. Коэффициенты
g1. Площадь фигуры, ограниченной экспонентами
g11. Максимальная из площадей двух фигур, одна из которых ограничена экспонентой
g2. Площадь фигуры, ограниченной экспонентами
h. Время установления — момент времени установления затухания колебаний не более величины 5% от разницы между установившимися значениями
j. Плавность затухания колебаний (скорость изменения ошибки):
Критерии b, c1, c2, d, e, f1, f2, g1, g11, g2 (см. рис. 1) отличаются от интегральных тем, что контролируют форму кривой переходного процесса, требуя ограничить кривую переходного процесса двумя экспонентами сверху и снизу.
Огибающие равномерно затухающего колебательного процесса суть экспоненты. Можно так сформулировать критерии качества переходного процесса, что будем косвенно влиять на форму кривой затухающего переходного процесса, приближая ее к идеальной (равномерное плавное затухание).
Оптимизационная задача решается итерационным методом. На каждом шаге задается определенный закон изменения eq(t) и путем расчета уравнений машины Парка-Горева определяется кривая переходного процесса напряжения генератора в переходном процессе, которая затем оценивается в соответствии с назначенным критерием качества. При неудовлетворительном качестве производится новая итерация при новом eq(t), и получается новая кривая переходного процесса. На каждом шаге подберем такие числа
Другой способ построения экспонент заложен в математической реализации критериев f2, g2. Предэкспоненциальный множитель задается постоянным. И Далее на каждом шаге решения оптимизационной задачи производится подбор коэффициента в показателе экспоненты в цикле: он увеличивается от нуля (что соответствует вырождению экспоненты в прямую линию, параллельную оси времени) до тех пор, пока экспоненты не коснутся кривой переходного процесса. В таком случае кривая переходного процесса никогда не выходит за пределы полученных экспонент. Размер шага цикла и погрешность подбора экспоненциальной кривой дискретному набору точек экстремумов кривой переходного процесса выбраны такими, чтобы скорость вычислений оптимизационной задачи с использованием критериев c1, c2, d, e, f1, g1, g11 и f2, g2 была сопоставима.
Однокритериальная оптимизация ЭДС возбуждения генератора для эффективного затухания переходного процесса напряжения на шинах не дают приемлемого результата, если использовать любой из критериев b, c1, c2, d, e, f1, f2, g1, g2, h, j. Только расчеты с помощью критериев «a» демонстрируют хороший результат (рис.2). Расчет, произведенный с помощью самой распространенной традиционной формы интегрального показателя ошибки
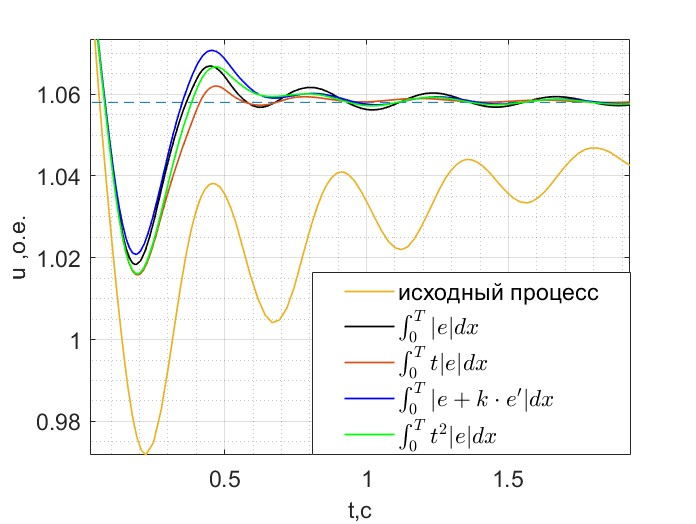
Рисунок 2 - Переходный процесс напряжения генератора до и после одноцелевой оптимизации с помощью традиционных интегральных критериев
4. Сужение множества Парето при многоцелевой оптимизации
Результатом применения к решению многоцелевой задачи ГА является фронт Парето — множество не улучшаемых по всем целевым функциям одновременно решений. При задаваемых в настоящей работе параметрах ГА количество точек на фронте Парето 650. О лучшем решении среди Парето-оптимальных решений можно говорить только в связи с предпочтениями исследователя. Для однозначного выбора лучшего для целей исследователя решения задачи многокритериальной оптимизации необходимо провести процедуру сужения множества Парето. Для этого может быть избран эвристический подход (визуально, по виду кривой фронта Парето) или аксиоматический (формализованная процедура). Вводится квант информации — информация от лица, принимающего решение (ЛПР) о том, выигрыш по какому критерию предпочтительнее. Затем в соответствии с расчетными формулами (данными, например, в
, , , ) следует пересчитать исходный векторный критерий с учетом кванта информации.Если обе цели с первого взгляда равнозначны, то введем дополнительные критерии сравнения решений. Рассмотрим 4 признака сравнения переходных процессов: просадка, размах, отклонение в 1 секунду и перерегулирование. Каждое решение Парето характеризуется своим набором этих чисел, т.е. для каждого решения Парето может быть задан четырёхкомпонентный вектор. Такие вектора в общем, скорее всего, уже не являются Парето-оптимальными. Произведем отбор из них Парето-оптимальных векторов.
Для дальнейшего сужения можно поступить различным образом.
1. Сравнение с эталоном. Выберем только те вектора, у которых все компоненты не хуже, чем у эталонного вектора.
2. Сужение множества Парето на основе разделения критериев сравнения по значимости. Будем считать время затухания более важным, чем остальные три. Выберем решения с минимальным временем затухания, а другие три критерия чтобы были не хуже, чем у эталона. Такое решение или одно, или нет таких.
3. Если предыдущее требование слишком жесткое, то выберем решения с минимальным временем затухания и только первым критерием не хуже эталона (или только вторым, или только четвертым).
4. На основе взаимно зависимой информации с использованием нелинейных функций .
5. На основе нечеткой информации о предпочтении ЛПР , .
Таблица 1 - Количество решений после сужение множества Парето
№ | Название расчета | Уникальных. решений | Уникальных. 4-х компонентных векторов | Разделения критериев на группы | |||||||
Все критерии не хуже эталона | tз=min, а критерии 1,2,4 не хуже эталона | tз=min, а критерий 1 не хуже эталона | tз=min, а критерий 2 не хуже эталона | tз=min, а критерий 4 не хуже эталона | На основе методики | На основе методики | На основе методики | ||||
1 | a1g2 | 458 | 213 | 0 | 0 | 1 | 1 | 0 | 1 | 2 | 137 |
2 | a3f2 | 616 | 145 | 2 | 0 | 1 | 1 | 0 | 1 | 3 | 145 |
3 | a3g2 | 541 | 108 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 28 |
4 | bh | 588 | 43 | 2 | 1 | 1 | 1 | 1 | 1 | 2 | 43 |
5 | с1f2, k=0,1 | 635 | 201 | 20 | 1 | 1 | 1 | 1 | 1 | 7 | 201 |
6 | c2f2, k =0,1 | 647 | 102 | 8 | 0 | 0 | 0 | 0 | 1 | 8 | 5 |
7 | c2f2, k=0,2 | 639 | 357 | 6 | 0 | 0 | 0 | 1 | 1 | 8 | 18 |
8 | c2f2, k=0,05 | 647 | 19 | 0 | 0 | 1 | 0 | 0 | 1 | 2 | 19 |
9 | c1g1 | 617 | 114 | 0 | 0 | 0 | 1 | 1 | 1 | 2 | 99 |
10 | c2g11 | 609 | 50 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 50(2) |
11 | c1g11 | 602 | 173 | 0 | 0 | 0 | 0 | 0 | 10 | 3 | 8 |
12 | c2h | 626 | 118 | 0 | 0 | 0 | 0 | 0 | 1 | 4 | 118 |
13 | a1f1 | 616 | 65 | 0 | 0 | 1 | 0 | 0 | 1 | 2 | 22 |
14 | be | 642 | 305 | 3 | 1 | 1 | 1 | 1 | 1 | 3 | 305 |
15 | bc2 | 647 | 286 | 3 | 1 | 1 | 1 | 1 | 1 | 2 | 286 |
16 | dh | 50 | 13 | 0 | 0 | 0 | 0 | 1 | 1 | 4 | 13 |
17 | eh | 588 | 288 | 0 | 0 | 0 | 0 | 1 | 1 | 4 | 133 |
18 | a1h | 582 | 212 | 0 | 0 | 1 | 1 | 0 | 1 | 2 | 212 |
19 | ej | 644 | 413 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 413 |
20 | a1j | 579 | 8 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 8 |
21 | g1j | 602 | 77 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 64 |
22 | g11j | 642 | 110 | 15 | 0 | 1 | 1 | 0 | 1 | 2 | 110 |
23 | a1f1c1 | 586 | 90 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 5 |
24 | a1f1c1, k=0,1 | 609 | 105 | 9 | 0 | 1 | 0 | 0 | 1 | 8 | 9 |
На рис.3, 4, 5, 6 приведены результаты, соответствующие табл.1, после сужения множества решений Парето до 1–3 точек.
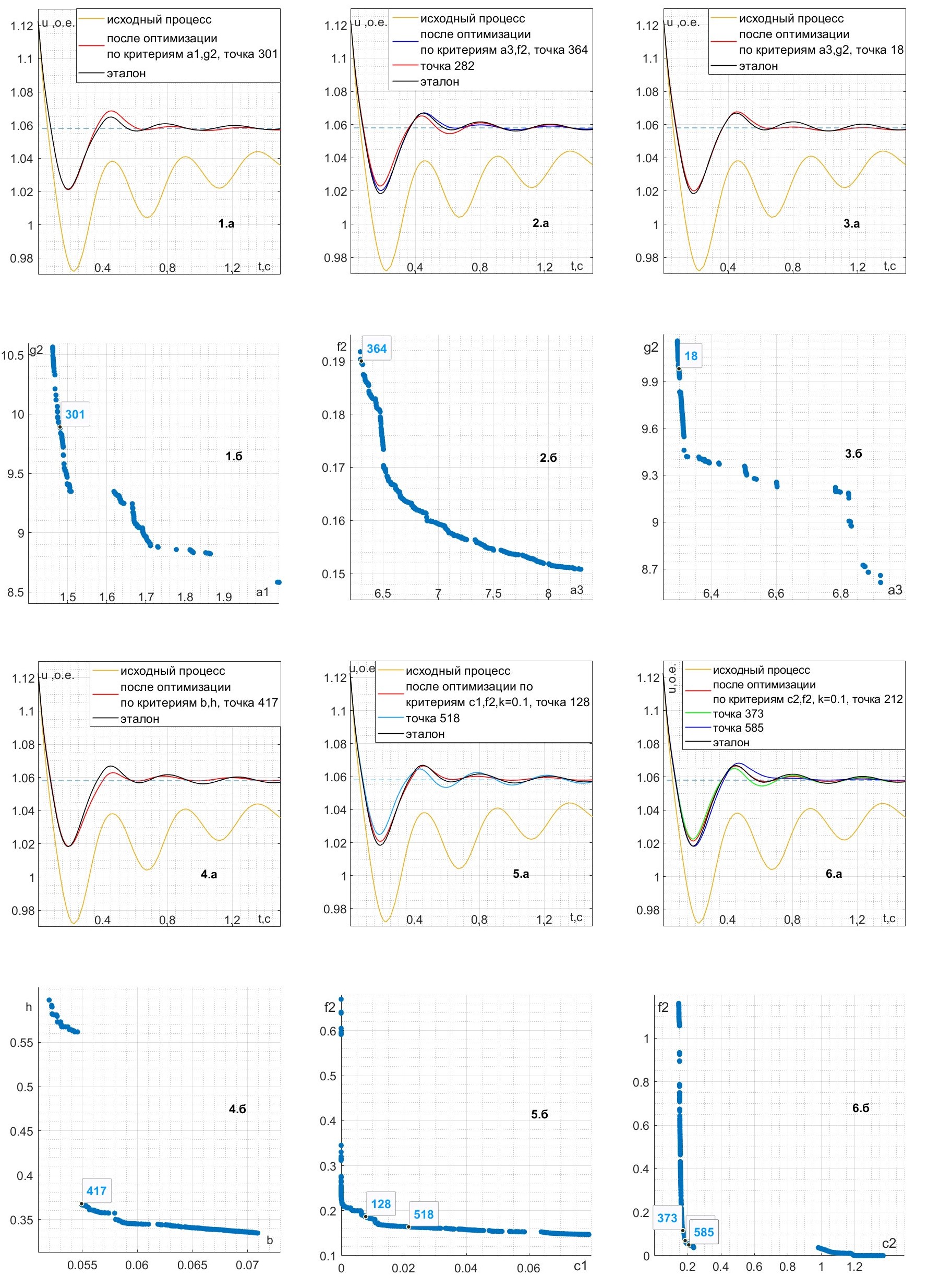
Рисунок 3 - Переходный процесс напряжения генератора до и после двухкритериальной оптимизации (1.а – 6.a) и соответствующие фронты Парето (1.б – 6.б)
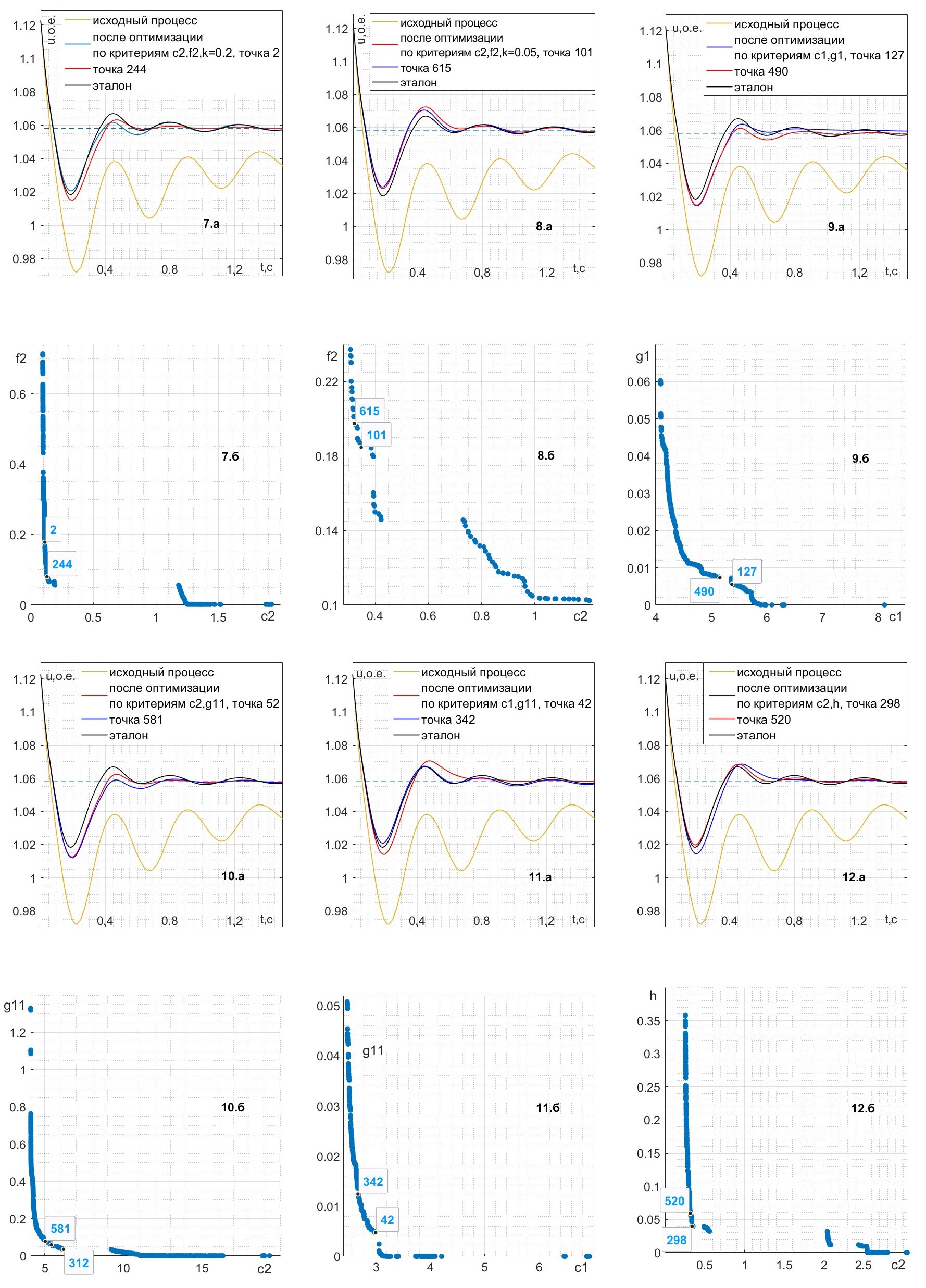
Рисунок 4 - Переходный процесс напряжения генератора до и после двухкритериальной оптимизации (7.а – 12.a) и соответствующие фронты Парето (7.б – 12.б)
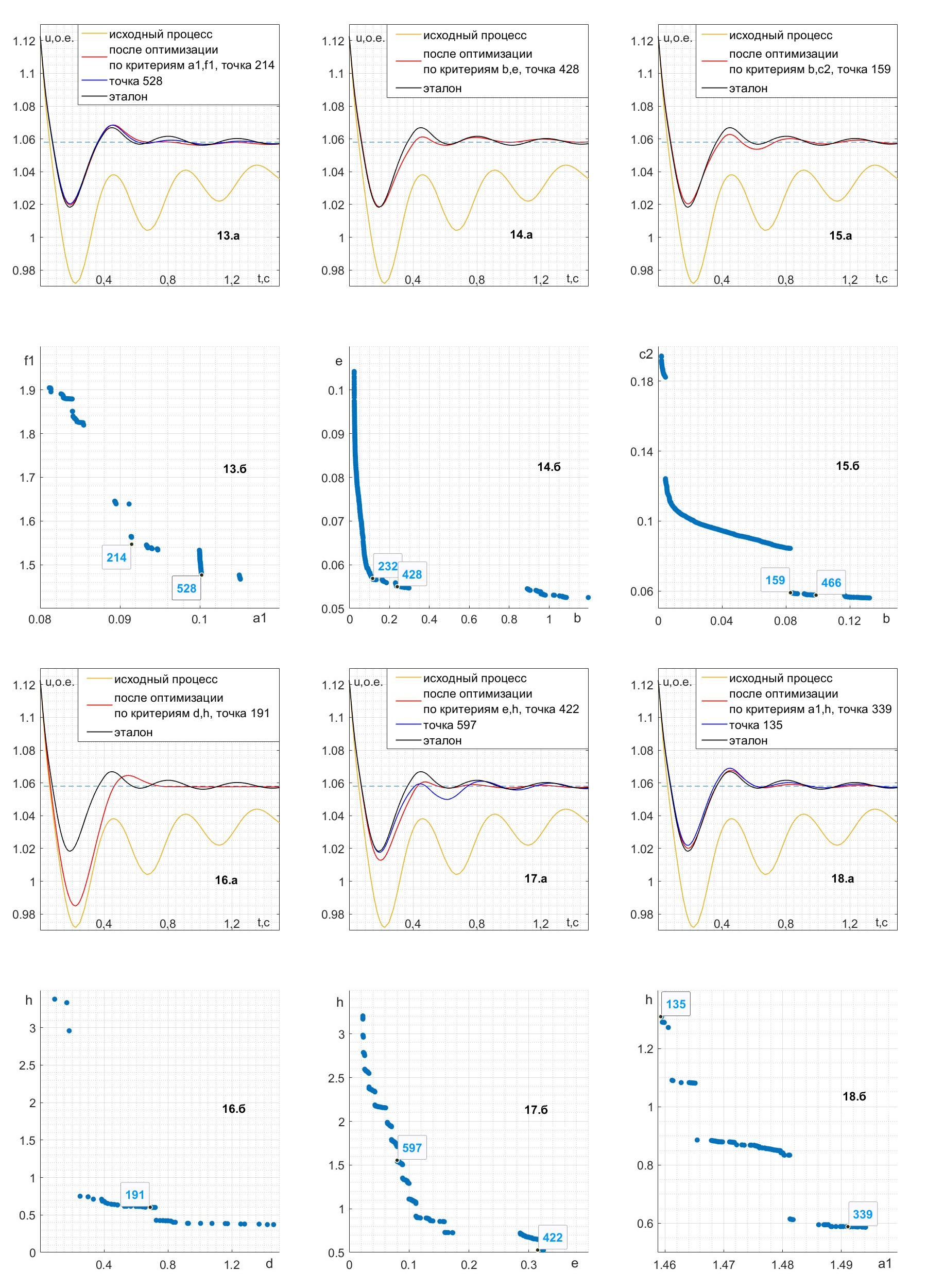
Рисунок 5 - Переходный процесс напряжения генератора до и после двухкритериальной оптимизации (13.а – 18.a) и соответствующие фронты Парето (13.б – 18.б)
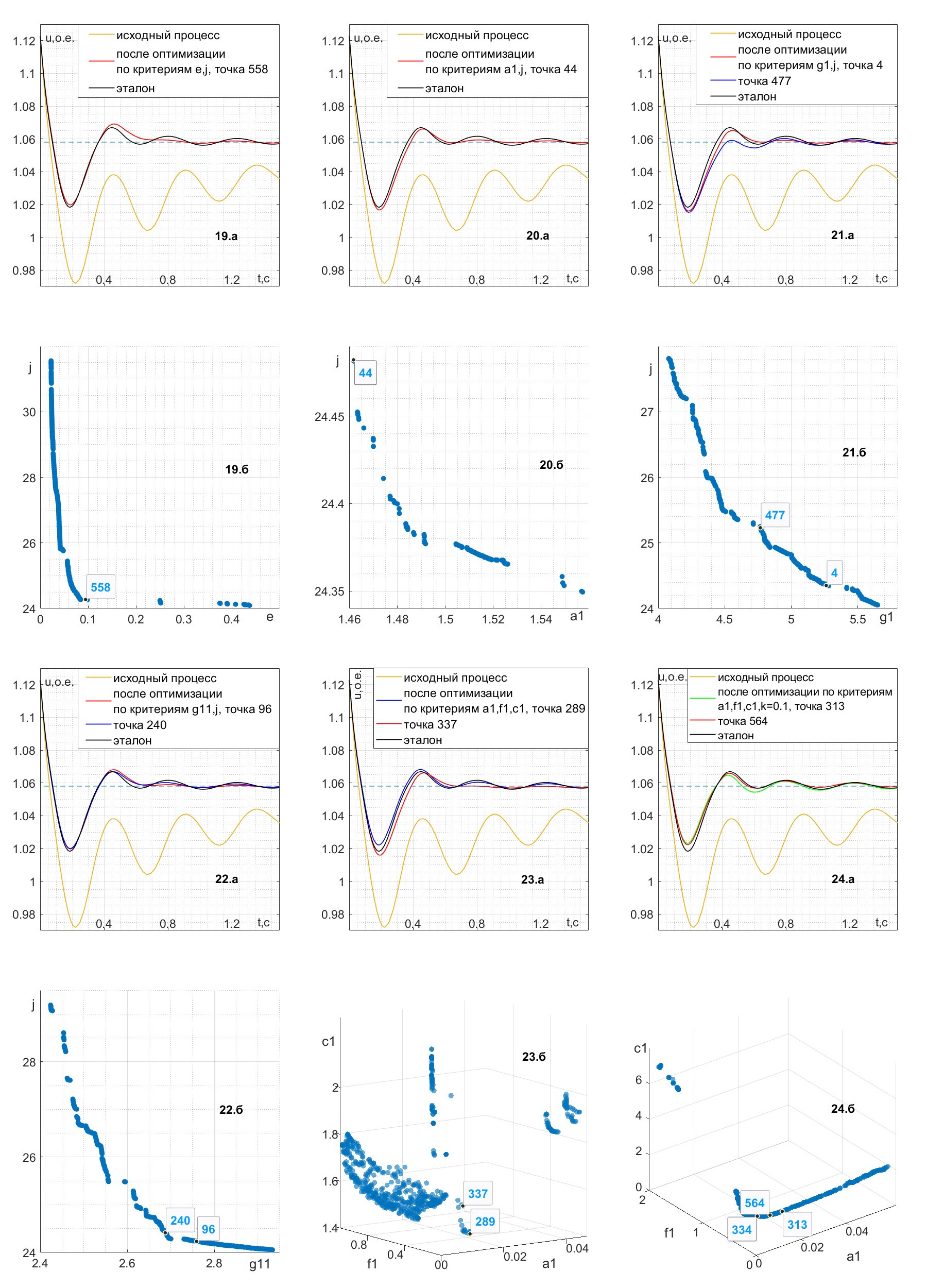
Рисунок 6 - Переходный процесс напряжения генератора до и после двух-или трехкритериальной оптимизации (19.а –24.a) и соответствующие фронты Парето (19.б –24.б)
Таблица 2 - Численные показатели переходных процессов после многокритериальной оптимизации
№ | Название расчета | Мин. значения | Размах колебаний | Откл. от уст. знач. при t=1c. | Перерегулирование |
1 | a1g2 | 1,0210 | 0,0476 | 0,12 | 0,0106 |
2 | a3f2 | 1,0203 | 0,0467 | 0,10 | 0,0090 |
3 | с1f2, k=0,1 | 1,0196 | 0,0472 | 0,10 | 0,0088 |
4 | c2f2, k=0,05 | 1,0235 | 0,0507 | 0,18 | 0,0162 |
5 | c1g1 | 1,0146 | 0,0464 | 0,10 | 0,0039 |
6 | c2g11 | 1,0126 | 0,0496 | 0,05 | 0,0042 |
7 | c2h | 1,0173 | 0,0512 | 0,07 | 0,0105 |
8 | be | 1,0185 | 0,0433 | 0,17 | 0,0038 |
9 | bc2 | 1,0208 | 0,0458 | 0,15 | 0,0085 |
10 | eh | 1,0118 | 0,0487 | 0,09 | 0,0025 |
11 | ej | 1,0197 | 0,0495 | 0,07 | 0,0111 |
12 | a1j | 1,0164 | 0,0502 | 0,06 | 0,0087 |
13 | g1j | 1,0160 | 0,0492 | 0,06 | 0,0072 |
14 | g11j | 1,0196 | 0,0485 | 0,09 | 0,0101 |
15 | a1f1c1, k=0,1 | 1,0182 | 0,0499 | 0,08 | 0,0101 |
Примечание: в относительных единицах
Все лучшие, выбранные с помощью методики сужения фронта Парето, точки дают примерно одинаковый результат — закон изменения eq(t), обеспечивающий приемлемый переходный процесс напряжения на шинах генератора (рис. 7).
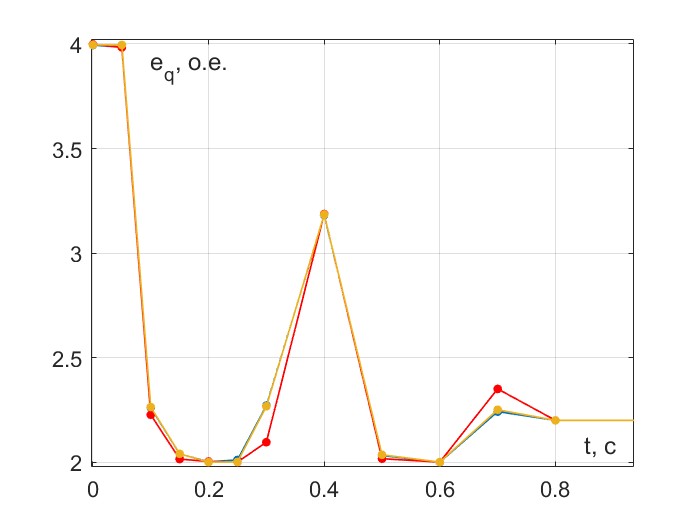
Рисунок 7 - Типовой закон изменения ЭДС возбуждения, обеспечивающий приемлемое затухание переходного процесса напряжения генератора
5. Заключение
На основе полученных результатов можно сделать следующие выводы:
· В тех случаях, когда фронт Парето не гладкий, а представляет собой набор отдельных точек и небольших кусков кривых, решение определяется однозначно визуально.
· В тех случаях, когда фронт Парето достаточно гладкий и без разрывов в своей срединной части, то решение выбрать достаточно сложно, поскольку они противоречивы: одни дают меньшую просадку или имеют меньший размах, другие интенсивнее или раньше затухают, третьи совсем лишены перерегулирования и представляют собой монотонно убывающую кривую, при этом дают большую просадку. Однозначный выбор с учетом предпочтений исследователя может быть произведен, например, с помощью методик сужения множества Парето, разработанных В. Д. Ногиным
, , , . А поскольку все рассмотренные постановки многокритериальных расчетов имеют одинаково значимые цели, то в соответствии с методикой сужения множества Парето для выбора «лучшего» решения необходимо введение новых критериев сравнения, дополнительной информации — «квант информации».· Способ построения ограничивающих экспонент существенно влиял на результат оптимизации.
· Критерии, которые сами по себе дают приемлемый результат при однокритериальной оптимизации, имело смысл включать в состав двухкритериальных расчетов, поскольку результат становился лучше (т.е. a1, a2, a3 были удовлетворительными, но a1g2 лучше, чем a1, a3f2 лучше, чем a3 и т.д.)
· Трехкритериальные расчеты имеют смысл только тогда, когда дают результат лучший, чем соответствующие двухкритериальные (но a1f1c1 лучше, чем a1f1).
· После проверки множества 4-хкомпонентных векторов проведенных 25 расчетов на Парето-оптимальность осталось 15 (см. табл.2). Эти 15 вариантов постановки задачи оптимизации равнозначны.
