Применение метода Ритца для расчета напряженно-деформированного состояния балок из материала с эффектом памяти формы
Применение метода Ритца для расчета напряженно-деформированного состояния балок из материала с эффектом памяти формы
Аннотация
Рассматривается применение метода Ритца для расчета балок, выполненных из материала с эффектом памяти формы. Функционал энергии деформации записывается для материала нитинол TiNi, обладающего физической нелинейностью, вызванной мартенситными превращениями в режиме прямого превращения под нагрузкой. Материал деформируется полностью в аустенитном состоянии при температуре выше температуры прямого мартенситного превращения. В качестве определяющих соотношений применялись уравнения структурно-аналитической мезомеханики. Определяющие соотношения записываются для макроуровня. Деформации микро и мезо-уровней учитываются с помощью операции ориентационного усреднения структурно-аналитической мезомеханики.
1. Введение
В настоящее время сплавы с эффектом памяти формы (ЭПФ) находят все большее применение в различных областях человеческой деятельности. Широкое применение они нашли в медицине, авиации, машиностроении, строительстве и др.
Сплавы с ЭПФ обладают уникальными свойствами, которые отсутствуют у большинства традиционных материалов, применяемых в промышленности. Однако, нетрадиционное поведение этих материалов требует новых моделей материала, при которых возможно применение традиционных методов механики деформированного твердого тела. Разработка теории и методов расчета инженерных конструкций, выполненных из материалов с ЭПФ, является актуальной задачей современных технологий.
2. Математическая модель
В настоящей работе используются определяющие соотношения деформационного типа, выведенные на основе общих уравнений структурно-аналитической мезомеханики
, , , . В рамках этого подхода были решены следующие краевые задачи: толстостенные трубы под внутренним давлением, стержневые статически неопределимые системы, ферменные конструкции, балки-стенки, квадратные пластины и пологие оболочки , , , . В данной работе применяется метод Ритца-Тимошенко для расчета статически неопределимых балок, выполненных из материалов с памятью формы, при произвольной нагрузке, с любыми закреплениями концов.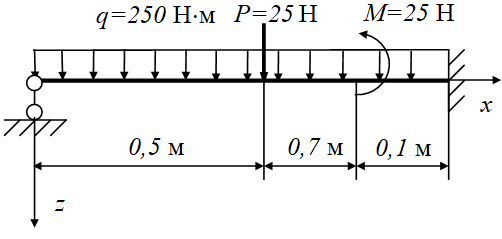
Рисунок 1 - Расчетная схема балки
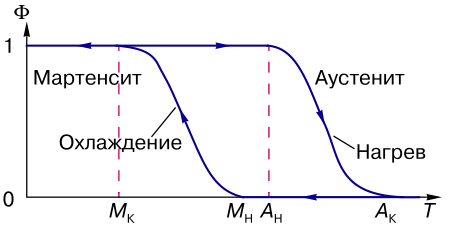
Рисунок 2 - Фазовые диаграммы для материалов с мартенситными превращениями:
МН, МK , AН, AK – характеристические температуры начала и конца превращения; Ф – объемная доля мартенсита
где σi – интенсивность напряжений; Е – модуль упругости; BФ – константа материала; ; T0 – температура термодинамического равновесия; q0 – тепловой эффект реакции; Di – дисторсия фазового превращения;
– напряжение начала прямого мартенситного превращения; TD – температура начала деформирования; MH, MK – температуры начала и конца прямого мартенситного превращения соответственно;
– напряжение конца мартенситного превращения,
; H(...) – функция Хевисайда.
Допущения, принятые при решении задачи:
1) модуль упругости материала в аустенитной и мартенситной фазах принимается одинаковым;
2) материал в условиях изотермического нагружения испытывает упругие и неупругие (фазовые) деформации;
3) для аппроксимации диаграммы деформирования принимается кубическая парабола.
По формулам модели структурно-аналитической мезомеханики
определим касательный модуль EK, максимальное напряжение σmax и фазовый предел текучести σT, определяющий начало прямого мартенситного превращения:В случае аппроксимации диаграммы материала кубической параболой (см.рис.3) определяющие соотношения примут вид :
,
,
.
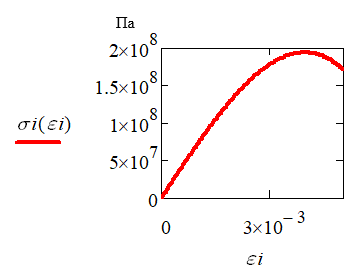
Рисунок 3 - Аппроксимация диаграммы деформирования материала TiNi кубической параболой
здесь EJy – изгибная жесткость балки, W(x)– прогиб, m – константа материала, xP, xM –координаты приложения сосредоточенной силы и момента соответственно; Jy=b⋅h3/12, Jn=b⋅h5/80; l – длина балки; b=l/7 м и h=2b – размеры поперечного сечения.
Параметры сплава TiNi, обладающего эффектом памяти формы представлены в таблице1.
3. Численная модель
Согласно методу Ритца прогиб балки в первом приближении представим в виде:
где φ(x) – аппроксимирующая функция, K – неопределенный коэффициент, представляющий собой амплитуду прогиба балки. Для построения функции φ(x) используем метод начальных параметров, что позволит учесть не только геометрические, но и силовые граничные условия. Начало координат выбираем на левом конце балки, ось х направим вправо, ось z – вниз. Согласно универсальному уравнению метода начальных параметров для балки с постоянной жесткостью, выражение для прогиба будет иметь вид:
здесь w0, φ0, M0, Q0 – начальные параметры, т.е. прогиб, угол поворота, изгибающий момент и поперечная сила в начале координат, aM=0,7 м, aP=0,5 м – координаты точки приложения момента M и силы P, соответственно.
В соответствии с рисунком 1 балка состоит из трех участков. На каждом из участков выражения для линии прогибов имеют вид:
Начальные параметры определяются исходя из граничных условий. На левой опоре имеем шарнирное закрепление w0=M0=0, на правой при x=l=0,8 м – жесткая заделка w3(l)=φ3(l)=0. Для определения φ3(l) требуется продифференцировать выражение для прогибов на третьем участке w3(x) и в полученное выражение подставить x=l. В результате для определения начальных параметров получаем следующую систему уравнений:
Решая эту систему уравнений при численных значениях коэффициентов получим: φ0=3,98/EJy, Q0=-90,4H. Найденные значения начальных параметров позволяют записать функции прогибов на каждом участке. Умножая выражения w1(x), w2(x), w3(x) на величину 24EJy/q получим окончательное выражение для аппроксимирующей функции прогиба:
Подставляя в (3) W(x)=Kφ(x), где φ(x) – функция, построенная методом начальных параметров (8), получим зависимость полной потенциальной энергии от параметра K:
где коэффициенты при параметре K определяются по формулам:
Интервал интегрирования в (9) следует разбить на три участка:
и в пределах каждого участка брать интегралы от производных соответствующих функций.
Минимизация полной потенциальной энергии балки по параметру K, приводит к нелинейному алгебраическому уравнению третьей степени относительно амплитуды прогиба K:
Решая полученное уравнение в системе Mathcad, получим K=0,0293.
4. Результаты
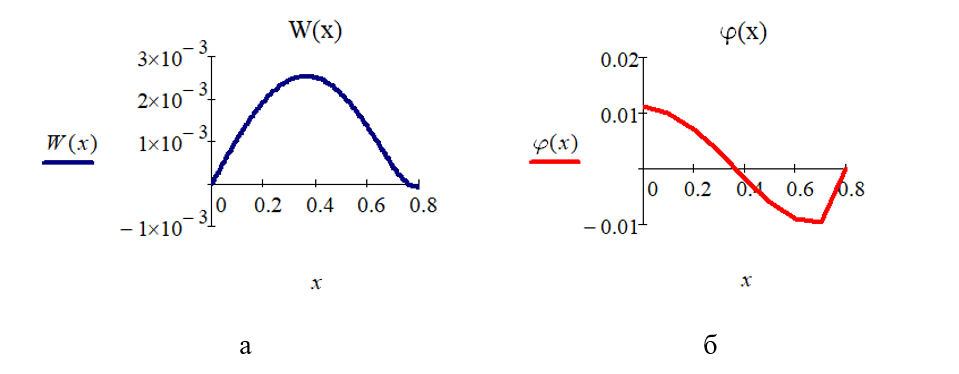
Рисунок 4 - Распределение прогиба W(x) (а) и угла поворота j(x) (б) по длине балки
Таблица 2 - Результаты расчета
Wmax×10-3, м | φmax×10-2 | Mmax×108 Нм | εmax×10-3 |
2,533 | 1,088 | 2,659 | 12,899 |
5. Заключение
В заключение можно отметить, что метод Ритца в сочетании с методом начальных параметров эффективен для расчетов балочных конструкций, выполненных из материалов с ЭПФ.
