ОБУЧЕНИЕ ФУНДАМЕНТАЛЬНЫМ ПОНЯТИЯМ МАТЕМАТИЧЕСКОГО АНАЛИЗА В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ НА ОСНОВЕ ИХ ОБРАЗНОГО ПРЕДСТАВЛЕНИЯ

ОБУЧЕНИЕ ФУНДАМЕНТАЛЬНЫМ ПОНЯТИЯМ МАТЕМАТИЧЕСКОГО АНАЛИЗА В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ НА ОСНОВЕ ИХ ОБРАЗНОГО ПРЕДСТАВЛЕНИЯ

Научная статья

Кисельников И.В.*

ORCID: 0000-0002-8086-8509,

Алтайский государственный педагогический университет, Барнаул, Россия

* Корреспондирующий автор (Kiselnikov_iv[at]altspu.ru)

Аннотация

Статья раскрывает проблему применения образного мышления в процессе изучения фундаментальных понятий математического анализа. К фундаментальным понятиям математического анализа отнесены: действительное число, функция, предел функции в точке, непрерывность функции. Отражено содержание представлений учащихся о фундаментальных математических понятиях математического анализа, возможности актуализации донаучных представлений учащихся. Указаны закономерности развития наглядных образов учащихся о математических понятиях. Выводы базируются на исследованиях представлений учащихся о математических понятиях. В работе раскрыты три типа образов учащихся о математических понятиях: геометрические, знаково-символические, художественные. Охарактеризована сущность этапов формирования фундаментальных математических понятий: этапа «житейских» представлений, этапа мономодальных математических представлений, этапа комплексных представлений, понятийного этапа, концептуального этапа. Указаны возможности использования различных форм представления математических понятий. Приведены схемы, демонстрирующие взаимосвязь математических понятий и идей в школьном курсе математики. Изложение теоретического материала сопровождено целесообразно подобранными примерами, иллюстрирующими использование образного мышления учащихся при изучении фундаментальных понятий математического анализа в курсе математики.

Ключевые слова: образное мышление; математическое образование; обучение математическим понятиям, фундаментальные математические понятия; понимание в обучении математике; качество обучения математике.

TEACHING FUNDAMENTAL CONCEPTS OF MATHEMATICAL ANALYSIS IN A SCHOOL MATHEMATICS COURSE BASED ON THEIR IMAGINATIVE REPRESENTATION

Research article

Kiselnikov I.V.

ORCID: 0000-0002-8086-8509,

Altai State Pedagogical University, Barnaul, Russia

* Корреспондирующий автор (Kiselnikov_iv[at]altspu.ru)

Abstract

The article discusses the problem of using imaginative thinking in the process of studying the fundamental concepts of mathematical analysis. The fundamental concepts of mathematical analysis include a real number, a function, the limit of function at a point, continuous function. The author describes the content of student ideas on the fundamental concepts of mathematical analysis, the possibility of realizing student pre-scientific ideas. The article also points out the regularities of the development of visual images of students about mathematical concepts. The conclusions are based on studies of student ideas about mathematical concepts. The paper identifies three types of images about mathematical concepts: geometric, symbolic, and artistic. The essence of the stages of the formation of fundamental mathematical concepts is characterized: the stage of routine conceptions, the stage of monomodal mathematical conceptions, the stage of complex conceptions, the notional stage, the conceptual stage. Also, the article indicates the possibilities of using various forms of representation of mathematical concepts and provides the diagrams demonstrating the interrelation of mathematical concepts and ideas in a school mathematics course. The presentation of the theoretical material is accompanied by appropriately selected examples illustrating the use of imaginative thinking of students in the study of fundamental concepts of mathematical analysis in mathematics courses.

Keywords: imaginative thinking; mathematical education; teaching mathematical concepts, fundamental mathematical concepts; understanding in teaching mathematics; quality of teaching mathematics.

Введение

В современной дидактике и психологии используются два основных подхода к изучению абстрактных понятий: операционный и актуализированный. Согласно теории поэтапного формирования умственных действий, реализующей операционный подход, усвоение математических понятий происходит в процессе осуществления определённых учебных действий. Такими действиями являются: подведения под понятие; выведения следствий; сравнения; классификации. Если действие не выполняется, то оно не усваивается. Выполнение разнообразных действий с признаками понятий может служить инструментом построения понятия, его порождения.

При актуализированном подходе к формированию понятия осуществляется работа, связанная с построением образа понятия. Этот образ развивается от отражения опытных представлений учащихся до более высоких степеней абстракции. При таком подходе основное внимание придаётся формированию ассоциаций житейских представлений обучаемых и усвоенных ранее знаний с новыми, подлежащими обучению.

Понятие о непрерывности функции может изучаться через построение ассоциации геометрических представлений об этом понятии с интуитивным представлением о непрерывности кривой – линии, которую можно повести свободным движением руки, не отрывая карандаша от бумаги. Среди других математических фактов, образы которых могут ассоциативно связываться в сознании учащихся, приведем следующие: предел функции в точке и значение функции в точке, аргумент функции и значение функции, разрыв функции в точке и непрерывность функции в точке. Эти примеры, во-первых, не исчерпывают всех возможных ассоциаций при изучении фундаментальных понятий математического анализа. Во-вторых, иллюстрируют лишь те ассоциации, которые могут быть преднамеренно построены в процессе обучения, причем не на первом этапе познания, а в дальнейшем. Если эти ассоциации не отвечают математическому смыслу понятия, то в дальнейшем это может привести к ошибочным выводам, неверным обобщениям. Это проявится в ошибках при решении задач, затруднениях при использовании этого понятия для дальнейшего построения теории.

В констатирующем эксперименте учащимся 10 класса средней общеобразовательной школы было предложено задание на выявление ассоциаций с терминами: стремление, соответствие, изменение, зависимость, движение (какие математические понятия возникают по ассоциации с этими терминами). Если «соответствие» связали с понятием функции около 90% человек, то с термином «зависимость» это понятие связывают лишь 40% учеников. при этом 60% затруднились с ответом. Этот пример показывает, что идея зависимости не работает несмотря на то, что в определении функции, которое дается в школьном курсе, встречается термин «зависимость». К такому же выводу приводит и тот факт, что у многих школьников вызывают затруднения задания на построение функций, моделирующих некоторую зависимость между величинами (физическими, геометрическими и др.), имеющиеся в действующих учебных пособиях. Следствиями этого являются трудности в решении задач на применение производной, которым программа по математике уделяет особое внимание.

Опора на образный компонент мышления, дающий возможности привлечь различные формы представления идей к формированию понятий, позволяет обеспечить процесс осознанного изучения фундаментальных математических понятий. Роль образности в развитии интеллекта человека отмечается в философской, психологической и педагогической научной литературе. «Образ – это субъективная картина мира или его фрагментов, включающая самого субъекта, пространственное окружение, временную последовательность событий» [1].

В научно- психологической литературе [1], [2], [3] отражаются разнообразные виды функций образов в процессе обучения:

• приобретение, хранение и репродуцирование информации;
• создание упреждающей программы поведения;
• эталонная функция;
• регулирование действий.

Образное мышление представляет собой деятельность, которая обеспечивает создание образов, оперирование ими, перекодирование их в заданном или произвольном порядке, использование различных систем отсчета для построения образов, выделение в образе различных признаков и значимых свойств.

В процессе обучения фундаментальным математическим понятиям образное мышление формируется под воздействием двух факторов: содержание понятий, условия и формы представления подлежащих изучению фактов; субъективная избирательность учащихся, их склонность к работе с образом, эмоциональное отношение к познаваемым фактам.

Обладание учащихся запасом исходных, простейших образов (конкретных функций: линейной, квадратичной, обратной пропорциональности; их графиков и свойств), представляющих информацию в различных формах, является условием успешного изучения начал математического анализа.

Наглядные образы делятся на три типа:

• геометрические (графические);
• знаково-символические;
• художественные.

Геометрические образы фиксируют свойства абстрактных объектов, отражая такие, как форма, величина, пространственная размещённость. В математическом анализе такими объектами являются функция, последовательность, предел функции, для которых геометрическая форма представления наиболее адекватна. Способность оперирования графическими образами присуща практически всем учащимся. Это подтверждает один из проведенных нами констатирующих экспериментов, когда учащимся еще до подробного изучения свойств функций, понятий предела и непрерывности было предложено задание, в котором были сгруппированы по три графика функций. Приведенные в каждой из групп функции обладали одним общим свойством. Учащимся требовалось дополнить каждую из этих групп четвертой функцией из представленного отдельно набора. Большинство учащихся (87%) верно выполнили задание.

Знаково-символическими образами отражаются общие свойства, операции и отношения, присущие идеальным объектам. Для последних характерен специфический набор элементов (цифры, буквы, условные знаки и др.), обозначение связи между ними, их пространственной размёщенности и взаимопринадлежности. Этот тип образов играет важное значение в формировании семиотической функции детей [4]. Изучение фундаментальных понятий математического анализа связано с формированием знаково-символических образов аналитических функций, пределов функций и др. Этот тип образов обеспечивает умение решать уравнения, неравенства, выполнять преобразования выражений, что имеет важное значение при изучении математического анализа.

Художественные образы характеризуются возможностью наиболее полно воспроизводить предметность объекта, все многообразие его признаков. Значимость для личности учащегося воспринимаемого объекта при создании художественного образа наиболее важна. При изучении фундаментальных понятий математического анализа этот тип образов способствует эмоционально-эстетическому восприятию фактов, что происходит за счет показа связи с какими-либо жизненными ситуациями, привлечения исторического материала, вызывающего интерес у школьника.

Методы и принципы исследования

Исследование выполнено на базе комплекса теоретических подходов и эмпирических методов, которые позволили выявить различные подходы к формированию математических понятий. Использованы методы обучения: анализ научной литературы по проблеме формирования математических понятий, изучение опыта преподавания математического анализа в школе, организация и проведение констатирующего эксперимента и качественная обработка его результатов.

Основные результаты

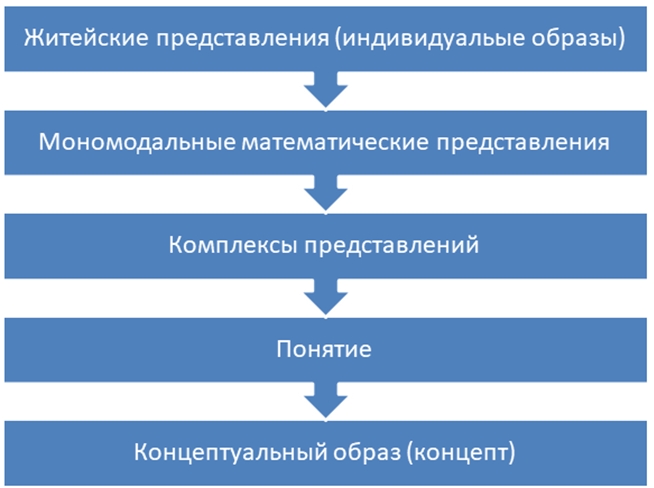
Начинать обучение фундаментальным понятиям математического анализа возможно с раскрытия заложенных в них первосмыслов. Поскольку достичь этого средствами только аналитического мышления затруднительно, важно, чтобы у учащихся был сформирован образ. На первом этапе – визуальный образ, который в последствии развивается до концептуального. При этом для познания каждого из понятий необходимо прохождение учащимся ряда этапов, которые можно представить в виде схемы (см. рисунок 1).

Рис. 1 – Схема формирования фундаментального математического понятия

 

Охарактеризуем сущность каждого из этапов формирования фундаментального математического понятия.

Этап житейских представлений

Без внимания к личностно-значимым психическим образованиям – стихийно образовавшимся донаучным «житейским» представлениям маловероятна возможность организации содержательного усвоения понятий, в силу отсутствия гарантий того, что представляемые вниманию учащегося факты будут им приняты безотносительно к имеющимся знаниям. В связи с этим подвергаются анализу «житейские» представления, связанные с терминами понятий с целью выяснения их адекватности научному смыслу понятий.

Этап мономодальных математических представлений

На этом этапе, основываясь на «житейских» представлениях, учащемуся в наиболее адекватной форме представляются объекты-представители объема понятия. Выбор той или иной формы для представления математического материала в школе обусловлен соответствием двум основным требованиям. Во-первых, представление содержания должно в наиболее ярком виде отражать сущность изучаемого понятия, то есть необходима адекватность с математической точки зрения. Во-вторых, эта форма должна способствовать развитию образа понятия, став первым этапом в понимании [5].

Этап комплексных представлений

Образы, в которых объекты отражаются в совокупности их свойств и отношений, называются комплексными представлениями [5]. В рамках таких представлений учащийся может переходить от анализа одних свойств объекта к анализу других его свойств, проявляя гибкость мышления.

Этап мономодальных математических представлений

Основываясь на комплексах представлений, отражающих в различных формах свойства математических объектов, выделяются существенные свойства. На этом этапе даются определения понятий на том уровне строгости, который отвечает целям обучения. Отрабатываются формальные процедуры оперирования понятием [6].

Концептуальный этап

На этом этапе формируется целостное содержание понятия, содержащее логический и интуитивный компоненты. Концепт не сводится к отдельным элементам представлений, а характеризуется осознанием смысла. Это обеспечивает применение понятия для построения другой теории, решения нестандартных задач, требующих самостоятельного выбора учащимся адекватной формы представления понятия, оптимального перевода содержания из одной формы представления в другие [7].

Реализация операционного подхода [8] дает хорошие результаты при изучении таких понятий, которые:

а) не противоречат житейским представлениям учащихся;

б) имеют первый уровень абстракции;

с) реализуются внутри одной дисциплины;

д) имеют образ, выражаемый в одной форме.

Операционный подход может быть использован, например, при изучении понятий евклидовой геометрии [9]. В процессе изучения фундаментальных понятий математического анализа операционный подход применим к формированию понятий, играющих вспомогательную роль. Например, интервала, аргумента функции, приращения функции в точке и др.

При изучении фундаментальных понятий математического анализа такой подход [10] менее пригоден для получения желаемых результатов. причины заключатся в следующем.

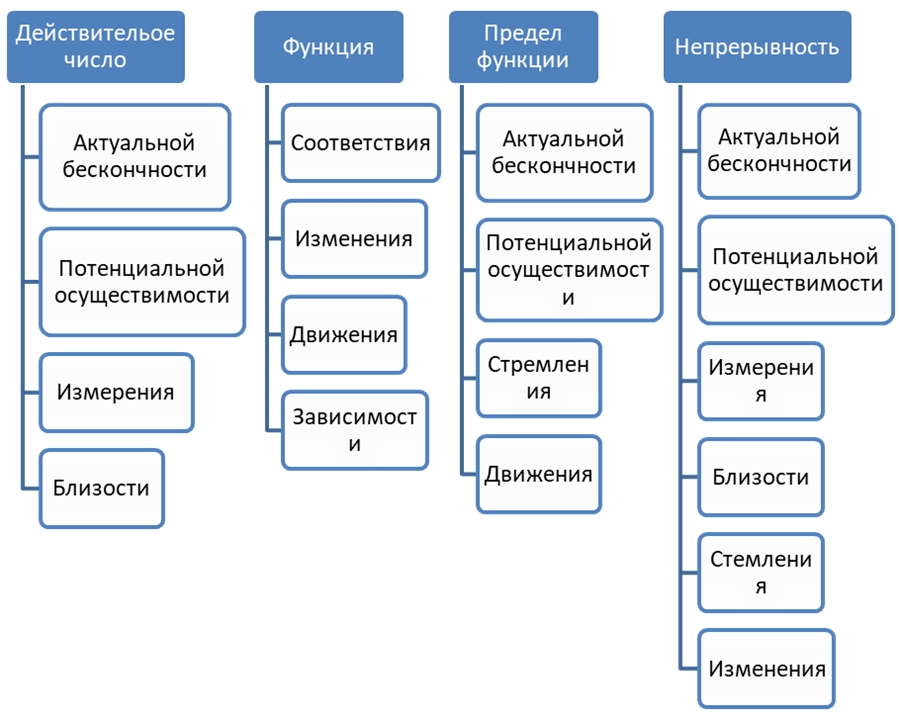
1. Познание понятий числа, функции, предела и непрерывности функции не ограничиваются рамками одной школьной дисциплины. Они носят характер метапредметных первосмыслов. Метапредметные первосмыслы – это ключевые фундаментальные объекты, имеющие свое проявление и проблематику в разных учебных дисциплинах (физике, химии, экономике, истории и других, как естественных, так и гуманитарных науках). Первосмысл – это ключевое понятие, категория, явление или иной объект, который концентрирует в себе достаточно широкую область знаний и выходит за рамки одной дисциплины. Другими примерами первосмыслов являются категории пространства, времени, движения; понятия буквы, ноты; стихии мира – огонь, вода, воздух, земля. К первосмыслам отнесем и идеи измерения, бесконечности, близости, симметрии, изменения, стремления, зависимости. Эти идеи тесно связаны с понятиями (см. рисунок 2).

Рис. 2 – Взаимосвязь понятий и идей в школьном курсе математического анализа

 

Процесс обучения фундаментальным понятиям математического анализа может быть построен таким образом, чтобы в ходе его осуществления была дана жизнь тем идеям, которые в их основе лежат. Это даст возможность: установить связи между изучаемыми понятиями, идеями и понятиями, идеями; приблизить теорию к практике ее применения. Возможность задействовать житейские представления в процессе обучения математическому анализу, строить ассоциации этих представлений с математическими представлениями при операционном подходе не рассматриваются. В соответствии с ней понятие можно считать усвоенным учеником, если он владеет существенными свойствами, умеет их использовать в процессе оперирования. В результате обучения у учащегося должна сложиться система знания – совокупность известных нам как основных, так и производных признаков мыслимых в понятии предметов, а также знания о том, в каких конкретных формах существуют содержащиеся в его объеме элементы. Однако, этим не исчерпываются знания о понятии. важным их элементом являются представления. Даже имея дело с сугубо абстрактными объектами, человек стремится внести в свои рассуждения элементы наглядности, конструируя для этой цели некоторые представления – наглядные модели объектов. Эти наглядные модели позволяют сделать зримыми идеи, лежащие в основе понятия.

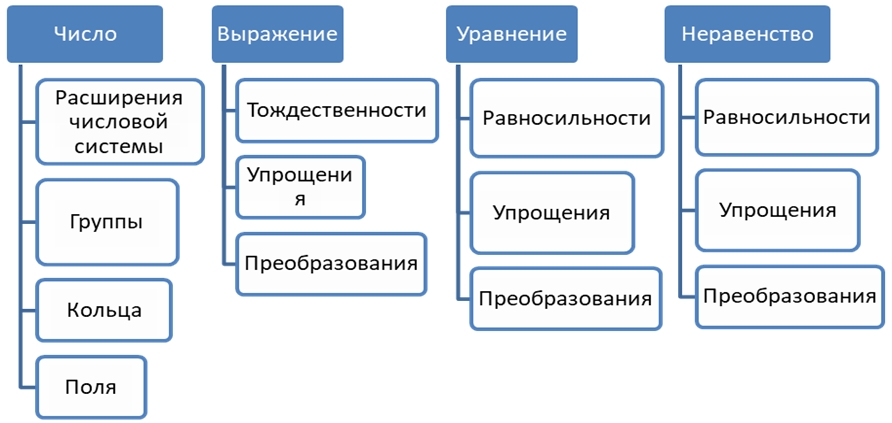
2. При изучении фундаментальных понятий математического анализа следует учитывать богатые выразительные возможности, которые имеются для их представления. Могут быть использованы различные формы: вербальная, знаково-символическая, графическая. Такого широкого спектра возможностей представления не имеет ни один другой раздел математики из изучаемых в школе. Для того, чтобы проиллюстрировать преимущества математического анализа в его фундаментальной части сравним его с изучаемым в школе алгебраическим материалом (см. рисунок 3).

 

Рис. 3 – Взаимосвязь понятий и идей в школьном курсе алгебры

 

Во-первых, большая часть алгебраических понятий и идей не имеют характер первосмыслов. Во-вторых, идеи, сопутствующие алгебраическим понятиям и фактам, выражаются преимущественно на знаково-символическом языке. Трудность освоения этого языка, невозможность его подкрепления более доступным для учащихся геометрическим приводят к тому, что возможность осознания смысла этих идей становится реальной ближе к окончанию изучения понятий курса. Условно-символические образы алгебраических идей складываются лишь на основе многократных преобразований, операций. Это сопряжено с затратами учебного времени. Принципиально иную картину имеем при изучении фундаментальных понятий математического анализа. Богатство выразительных средств для представления его идей, отсутствие необходимости предварительного усвоения операционной стороны дает возможность осуществлять их изучение раньше – до знакомства с понятием, на самом первом этапе. При этом освоение идей наступает раньше, чем освоение полного содержания понятия. Это создает базу для понимания. именно наглядно представленные идеи и выступают таким средством для ученика.

3. Житейские представления учащихся, ассоциированные с терминами зависимость, соответствие, стремление, предел, непрерывность и т.д., сложившиеся ко времени изучения начал математического анализа большей частью стихийно, характеризуются размытостью, нечеткостью, неполнотой с одной стороны и индивидуальностью, личной значимостью – с другой. переход от житейских представлений через определение к понятию не может быть осуществлен по операционной схеме, поскольку осуществляемые действия не могут быть сразу соотнесены с индивидуальными образами. Необходимо предварительно провести работу по доведению индивидуальных образов до такого уровня, когда они будут характеризоваться четкостью, позволяющей выделить свойства понятия. Игнорирование индивидуальных образов, ранний переход к абстракциям ведет к тому, что у учеников формируются неадекватные представления, хотя формальные знания ученик демонстрирует. Например, решая неравенство методом интервалов допускаются технические ошибки, причиной которых является привычка определять знак функции на различных интервалах непосредственной подстановкой, в то время как метод анализа изменения знаков является более надежным.

Представления учащихся выполняют важную функцию не только на первом этапе изучения понятий, но и на завершающем: для применения к решению прикладных задач, использования их в нестандартных ситуациях [11]. В ходе поиска решения задач, когда рассуждения проводятся вслепую, наощупь, неизвестно, какие из них понадобятся для решения, успех обеспечивает владение представлениями содержания в различных формах. Гибкость мышления обеспечивают комплексы представлений, содержащие информацию о понятии в вербальной, графической, знаково-символической формах, позволяющие осуществлять перевод содержания из одной формы в другую [12], [13].

Заключение

Исследование применения образного мышления при изучении фундаментальных понятий математического анализа в школьном курсе математики позволяет сделать следующие выводы.

1. Понятия формируются поэтапно

Формирование фундаментальных понятий математического анализа может осуществляться на основе актуализации интуитивных представлений, а в дальнейшем – постепенного совершенствования образов этих понятий (от отражения в представлениях математического содержания, выраженного в одной форме, к комплексному представлению в различных формах, а от него к целостному концептуальному представлению). В процессе обучения учащийся должен пройти через ряд этапов от житейских представлений до концептуального понимания.

2. В процессе формирования понятий осуществляется перевод содержания на различные языки представления

Необходимость формирования у школьников гибкого мышления, в основе которого лежат комплексы представлений содержания фундаментальных понятий математического анализа, служит причиной специального рассмотрения перевода математического содержания на различные языки представления.

3. Для формирования понятий используются специальные методические средства

Анализ научной психолого-педагогической литературы, касающейся проблемы формирования математических понятий, приводит к осознанию необходимости выбора методических средств для формирования целостных образов фундаментальных понятий математического анализа. Таким средством могут выступать специальные задания, задачи и упражнения.

4. Формирование фундаментальных математических понятий осуществляется на основе образного мышления учащихся

К формированию фундаментальных понятий математического анализа возможно привлечь средства образного мышления. В образах фиксируется: идейный смысл, благодаря которому осознанно осуществляется оперирование понятием, применение его для решения нестандартных задач, субъективно переработанный опыт. Невозможно создавать и удерживать образ, тем более оперировать образом, к содержанию которого субъект безразличен. 

Финансирование Работа выполнена при финансовой поддержке Алтайского государственного педагогического университета.	Funding This work was financially supported by the Altai State Pedagogical University.
Благодарности Автор выражает благодарность своему научному руководителю профессору Е. И. Лященко (г. Санкт- Петербург) за обсуждение идей исследования.	Acknowledgement The author expresses his gratitude to his supervisor, Professor E. I. Lyashchenko (St. Petersburg) for a discussion of the research ideas.
Конфликт интересов Не указан.	Conflict of Interest None declared

Список литературы / References

1. Ганзен В. А. Восприятие целостных объектов / В. А. Ганзен, Ленинград, 1974, 152 с., З. 24.
2. Korrea, R. I. Maestros: de la tiza al bit / R. I. Korrea, M. Gusman-Franko // Comunicar, 16, 181–187. DOI: 10.3916/C16-2001-25.
3. Hester de Boer. Long-term effects of metacognitive strategy instruction on student academic performance: A meta-analysis / Hester de Boer, Anouk S. Donker, Danny D.N.M. Kostons et al. // Educational Research Review, Volume 24, 2018, Pages 98-115. DOI: 1016/j.edurev.2018.03.002
4. Знаков В. В. Психология понимания: проблемы перспективы / В. В. Знаков. - М .: Изд-во «Институт психологии РАН», 2005. - 448 с.
5. Бахмутский А. Е. Содержание результатов общего образования и деятельность учителя / А. Е. Бахмутский // Известия РГПУ им. А.И. Герцена. - Санкт-Петербург, 2012, № 148, стр. 77–86.
6. Кулешова И. Г. Содержание фаз понимания учебного материала / И. Г. Кулешова, Э. К. Брейтигам // Наука для образования сегодня. - 2019. - Т. 9 - № 5. - С. 97–109
7. Mutsumi Imai. The relation between language, culture, and thought / Mutsumi Imai, Junko Kanero, Takahiko Masuda // Current Opinion in Psychology. Volume 8. 2016. Pages 70-77. DOI: 10.1016/j.copsyc.2015.10.011
8. Bloom B. A. Taxonomy of Educational Goals, Handbook 1: Cognitive domain / B. A. Bloom. New York: David McKay, 1956.
9. Shrivers M. Gaining Insight Into Human Nature: A Review of Literature Classroom Intervention Studies / M. Shrivers, T. Janssen, O. Fialho et al. // Review of Research in Education, 2019, Vol. 89, issue 1. - DOI: 3102/0034654318812914
10. Кисельников И. В. Процессный подход в обеспечении качества обучения математике в общеобразовательной школе / И. В. Кисельников // Мир науки, культуры, образования: научный журнал, 2010, № 1. c.148-151.
11. Подходова Н. С. Понимание при обучении математике: Необходимые условия достижения / Н. С. Подходова // Герценовские чтения": к 95-летию кафедры методы обучения математике и информатике. Российский государственный педагогический университет им. А. И. Герцена. - 2015. - С. 119-131.
12. Weinberg, P. J. Supporting Mechanistic Reasoning in Domain-Specific Contexts / P. J. Weinberg, // Journal of Pre-College Engineering Education Research (J-PEER), 7(2), Article 3. DOI: 7771/2157-9288.1127
13. TIMSS 2019 Assessment Frameworks / Mullis, I. V. S., Martin, M. O. Eds. 2017. [Electronic resource]. URL: http://timssandpirls.bc.edu/timss2019/frameworks/ (accessed 20.01.2022)

Список литературы на английском языке / References in English

1. Hansen V. A. Vosprijatie celostnykh ob"ektov [Perception of integral objects] / V. A. Ganzen, Leningrad, 1974, 152 p., 24 [in Russian]
2. Korrea, R. I. Maestros: de la tiza al bit [Masters: from chalk to bit] / R. I. Korrea, M. Gusman-Franko // Comunicar [Communicate], 16, 181–187. DOI: 10.3916/C16-2001-25 [in Spanish]
3. Hester de Boer. Long-term effects of metacognitive strategy instruction on student academic performance: A meta-analysis / Hester de Boer, Anouk S. Donker, Danny D.N.M. Kostons et al. // Educational Research Review, Volume 24, 2018, Pages 98-115. DOI: 1016/j.edurev.2018.03.002
4. Znakov V. V. Psikhologija ponimanija: problemy perspektivy [Psychology of understanding: problems of perspective] / V. V. Znakov. - Moscow: «Institut psikhologii RAN», 2005. - 448 p. [in Russian]
5. Bakhmutsky A. E. Soderzhanie rezul'tatov obshhego obrazovanija i dejatel'nost' uchitelja [The content of the results of general education and the activity of the teacher] / A. E. Bakhmutsky // Izvestija RGPU im. A.I. Gercena [Izvestia: Herzen University Journal of Humanities & Sciences]. - St. Petersburg, 2012, No. 148, pp. 77-86 [in Russian]
6. Kuleshova I. G. Soderzhanie faz ponimanija uchebnogo materiala [The content of the phases of understanding educational material / I. G. Kuleshova, E. K. Breitigam // Nauka dlja obrazovanija segodnja [Science for Education today].- 2019.- Vol. 9 - No. 5. - pp. 97-109 [in Russian]
7. Mutsumi Imai. The relation between language, culture, and thought / Mutsumi Imai, Junko Kanero, Takahiko Masuda // Current Opinion in Psychology. Volume 8. 2016. Pages 70-77. DOI: 10.1016/j.copsyc.2015.10.011
8. Bloom B. A. Taxonomy of Educational Goals, Handbook 1: Cognitive domain / B. A. Bloom. New York: David McKay, 1956.
9. Shrivers M. Gaining Insight Into Human Nature: A Review of Literature Classroom Intervention Studies / M. Shrivers, T. Janssen, O. Fialho et al. // Review of Research in Education, 2019, Vol. 89, issue 1. - DOI: 3102/0034654318812914
10. Kiselnikov I. V. Processnyjj podkhod v obespechenii kachestva obuchenija matematike v obshheobrazovatel'nojj shkole [The process approach in ensuring the quality of teaching mathematics in secondary schools] / I. V. Kiselnikov // Mir nauki, kul'tury, obrazovanija: nauchnyjj zhurnal [The World of Science, Culture, Education: scientific journal], 2010, No. 1. pp.148-151. [in Russian]
11. Podkhodova N. S. Ponimanie pri obuchenii matematike: Neobkhodimye uslovija dostizhenija "68 Gercenovskie chtenija": k 95-letiju kafedry metody obuchenija matematike i informatike [Understanding in teaching mathematics: Necessary conditions for achieving "68 Herzen readings": dedicated to the 95th anniversary of the Department methods of teaching mathematics and computer science] / N. S. Podkhodova. Herzen University. - 2015. - pp. 119-131. [in Russian].
12. Weinberg, P. J. Supporting Mechanistic Reasoning in Domain-Specific Contexts / P. J. Weinberg, // Journal of Pre-College Engineering Education Research (J-PEER), 7(2), Article 3. DOI: 7771/2157-9288.1127
13. TIMSS 2019 Assessment Frameworks / Mullis, I. V. S., Martin, M. O. Eds. 2017. [Electronic resource]. URL: http://timssandpirls.bc.edu/timss2019/frameworks/ (accessed 20.01.2022)