УВЕЛИЧЕНИЕ ПРОИЗВОДИТЕЛЬНОСТИ ЭЛЕКТРОЭРОЗИОННОГО ПРОФИЛИРОВАНИЯ АЛМАЗНЫХ ШЛИФОВАЛЬНЫХ КРУГОВ
Рубанов М.Ю.
Студент, Пензенский государственный университет
УВЕЛИЧЕНИЕ ПРОИЗВОДИТЕЛЬНОСТИ ЭЛЕКТРОЭРОЗИОННОГО ПРОФИЛИРОВАНИЯ АЛМАЗНЫХ ШЛИФОВАЛЬНЫХ КРУГОВ
Аннотация
В статье рассмотрены возможности использования алгоритма поиска экстремума на основе рекуррентного метода наименьших квадратов в системе экстремального регулирования процесса профилирования алмазных шлифовальных кругов, а также приведены результаты математического моделирования, доказывающие, что использование данного алгоритма позволяет увеличить производительность обработки.
Ключевые слова: автоматическое управление, экстремальный регулятор, производительность.
Rubanov M.Y.
Student, Penza State University
INCREASE IN PRODUCTIVITY OF ELECTROEROSIVE PROFILING OF DIAMOND GRINDING CIRCLES
Abstract
In article possibilities of use of algorithm of search of an extremum on the basis of a recurrent method of the smallest squares in system of extreme regulation of process of profiling of diamond grinding circles are considered, and also the results of mathematical modeling proving are given that use of this algorithm allows to increase processing productivity.
Keywords: automatic control, extreme regulator, productivity.
При профилировании алмазных шлифовальных кругов выбор элекроэрозионного метода обработки является оправданным по сравнению с механическими методами по причине большой твердости обрабатываемых поверхностей. Важнейшим направлением совершенствования процесса электроэрозионного профилирования является его автоматизация. Система автоматического управления должна обеспечивать требуемые показатели качества обрабатываемой поверхности при максимальной производительности обработки. Для управления данным процессом требуется использование систем, способных адаптироваться к изменениям параметров обработки [1].
Для решения этой проблемы предлагается использовать систему экстремального управления. Существующие системы регулирования электроэрозионной обработки не обеспечивают соответствующей современным требованиям общества производительности. Для удовлетворения этих требований предлагается использовать систему экстремального регулирования мощности, выделяемой в межэлектродном зазоре, которая обеспечит повышение производительности на 40 – 60%.
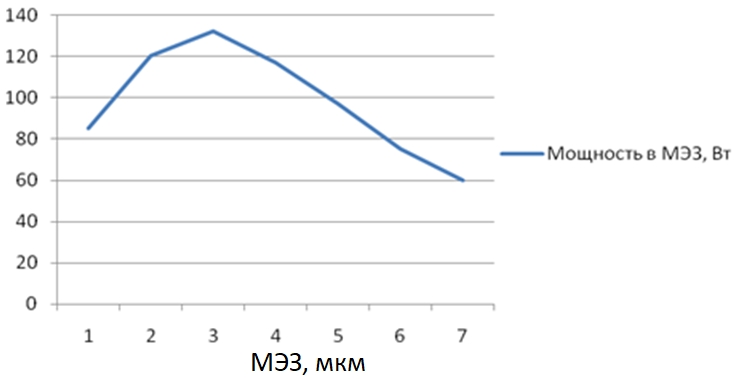
Экспериментально установлено, что мощность, выделяемая в межэлектродном зазоре, имеет экстремальную зависимость от величины межэлектродного зазора (рис.1).
Рис.1 – Зависимость мощности от величины межэлектродного зазора
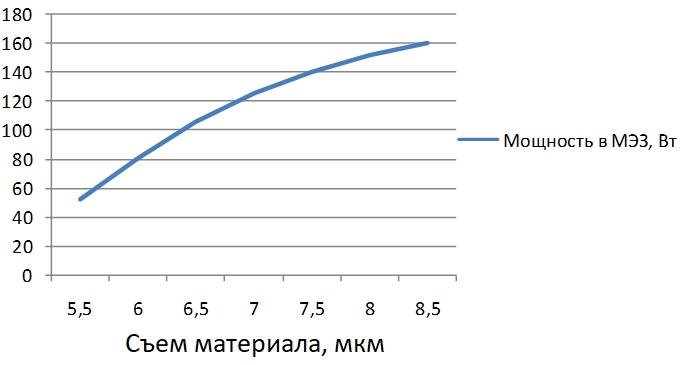
Производительность процесса электроэрозионной обработки увеличивается с увеличением мощности, выделяемой в межэлектродном зазоре (рис. 2).
Рис.2 – Зависимость производительности электроэрозионной обработки от мощности, выделяемой в межэлектродном зазоре
Представленные зависимости позволяют сделать вывод о том, что выполнение задачи дипломного проектирования по максимизации производительности электроэрозионной обработки возможно при регулировании подачи электрода таким образом, чтобы в межэлектродном зазоре выделялась максимальная мощность.
Системы экстремального регулирования электроэрозионной обработки разрабатывались и ранее, однако недостатком существующих систем является их высокая чувствительность к внешним возмущающим факторам. Это обусловлено несовершенством алгоритмов поиска экстремума.
Выгодным режимом работы системы будет создание автоколебаний вблизи экстремального значения. Параметры автоколебаний (амплитуда а, частота w, начальное смещение х0) определяются по методу гармонической линеаризации. Были получены следующие выражения для параметров автоколебаний:
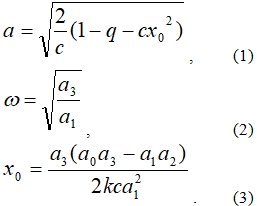
Для устранения статической ошибки в системе предлагается менять знак обратной связи с «плюса» на «минус» и обратно в зависимости от знака статической ошибки. Для этого в систему вводится переключатель знака обратной связи с «плюса» на «минус» и наоборот.
Важной проблемой при исследовании системы, содержащей элементы с нелинейной экстремальной характеристикой, является определение положения рабочей точки на экстремальной характеристике. Эта задача затрудняется невозможностью отделения линейной части системы от нелинейной. Предлагается дополнительно к поиску экстремума автоколебательным способом использовать алгоритм, который предусматривает вычисление коэффициента передачи по рекуррентному методу наименьших квадратов (РМНК). Алгоритм состоит из следующих последовательно выполняемых действий [2]:
- считать с модели входной u(k) и выходной y(k) сигналы экстремального объекта;
- вычислить коэффициенты АРСС-модели ai и bj по рекуррентному методу наименьших квадратов;
- по найденным значениям коэффициентов вычислить коэффициент на основании теоремы о конечном значении дискретной передаточной функции:
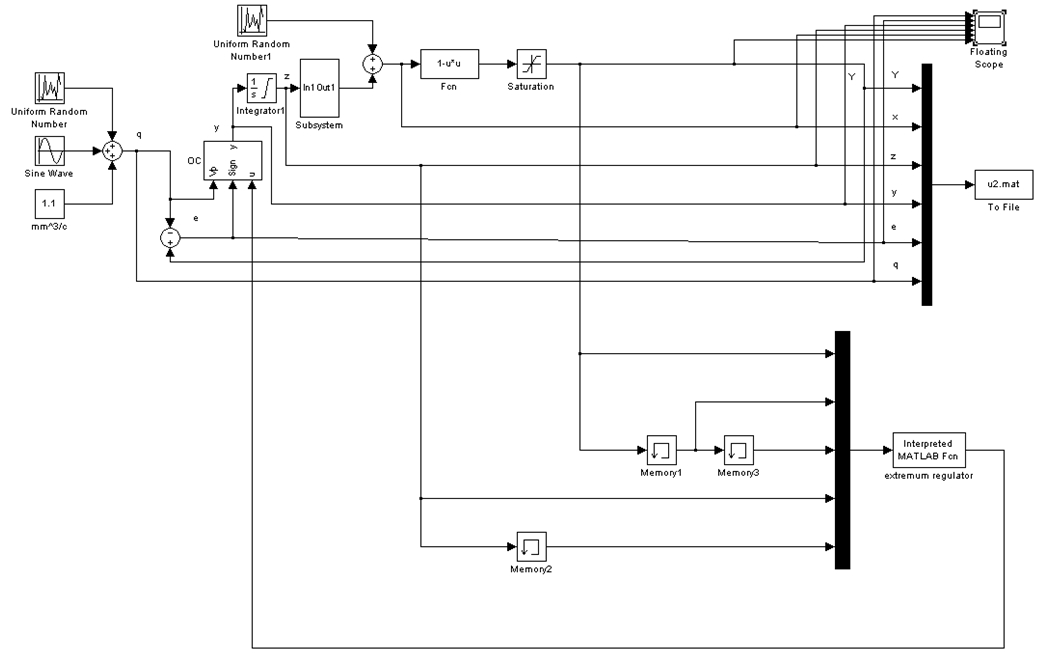
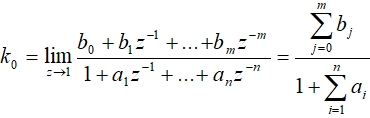 (4) Для проверки алгоритма соберем Simulink-модель в системе MatLab. Модель представлена на рисунке 3.
(4) Для проверки алгоритма соберем Simulink-модель в системе MatLab. Модель представлена на рисунке 3.
Рис. 3 – Модель системы экстремального регулирования с реализованным алгоритмом по РМНК
Анализ полученных результатов позволяет сделать вывод, что даже при действии сильных помех, уровень которых соизмерим с уровнем входного сигнала, система экстремального регулирования удерживает координаты объекта в области экстремальных значений его целевой функции. Несмотря на высокий уровень помех, отклонение системы от точки экстремума не превышает 12%, что подтверждает эффективность предлагаемого алгоритма.
Список литературы
Фомин В.Н. Адаптивное управление динамическими объектами / В.Н.Фомин, А.Л. Фрадков, В.А. Якубович. - М.: Высшая школа, 1981. – 448 с.
Изерман Р. Цифровые системы управления. – М.: Мир, 1984. – 541 с.