СРАВНЕНИЕ МЕТОДОВ АГЕНТНОГО МОДЕЛИРОВАНИЯ НА ПРИМЕРЕ ИГРЫ В РАЗНОВИДНОСТЬ ПОКЕРА «ТЕХАССКИЙ ХОЛДЕМ»
СРАВНЕНИЕ МЕТОДОВ АГЕНТНОГО МОДЕЛИРОВАНИЯ НА ПРИМЕРЕ ИГРЫ В РАЗНОВИДНОСТЬ ПОКЕРА «ТЕХАССКИЙ ХОЛДЕМ»
Научная статья
Лаврик А.Е.1, *, Тропченко А.А.2
Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики, Санкт-Петербург, Россия
* Корреспондирующий автор (56111[at]mail.ru)
АннотацияМетоды агентного обучения стремительно набирают популярность в исследованиях, но поиски новых методов для практического применения в задачах с неполной информацией все еще активно ведутся. Игра в разновидность покера “Техасский холдем” является одной из самых удобных задач для проведения исследования т.к. все еще является нерешенной и является показательным примером мультиагентной системы с неполной информацией. В данной статье проводится сравнительный анализ методов агентного моделирования при помощи обучения алгоритмов игре в разновидность покера «Техасский холдем». Данное исследование ставит своей целью показать слабые и сильные стороны различных подходов в обучении агента. В исследовании применяются алгоритмы использующие нейронные сети для обучения и численные методы решения задач. Результатом исследования является данные по скорости обучения и результатам игры с шагом по эпохам обучения.
Ключевые слова: Нейронные Сети, обучение с подкреплением, Агент, Покер.
A COMPARISON OF AGENT-BASED MODELING METHODS VIA TEXAS HOLD 'EM
Research article
Lavrik A.E.1, *, Tropchenko A.A.2
ITMO University, Saint Petersburg, Russia
* Corresponding author (56111[at]mail.ru)
AbstractAgent-based learning methods are rapidly gaining popularity in research, but the search for new methods for practical application in problems with incomplete information is still actively underway. Playing the Texas Hold'em poker is one of the most convenient tasks for conducting research, as it is still unsolved and is a good example of a multi-agent system with incomplete information. The current study presents a comparative analysis of the methods of agent-based modeling by teaching algorithms to play Texas Hold'em poker. This study aims to demonstrate the strengths and weaknesses of different approaches to agent training with the help of algorithms that use neural networks for training and numerical methods for solving problems. The results of the study are presented in the form of data on the learning rate and the results of the game in epoch increments.
Keywords: Neural Networks, Reinforcement learning, Agent, Poker.
ВведениеЦелью данной работы является повышение эффективности прогнозирования игровых ситуаций мультиагентными системами с использованием технологий искусственного интеллекта.
Искусственный интеллект стремительно совершенствуется. За последние два десятилетия алгоритмы машинного обучения превзошли лучших мировых игроков таких играх, как: нарды, шашки, шахматы, «Своя Игра» (Jeopardy!), видеоигры Atari [1]. Известная победа в Го, стала одним из главных прорывов в области машинного обучения в играх за последние годы. Решения данных задач приводит к открытию новых методов работы с данными и обучения ИИ, что очень важно для науки, поэтому ежегодно проводится множество соревнований для машин, где люди пытаются совершенствовать алгоритмы, внедрять новейшие подходы, исследовать и сравнивать существующие методы работы с данными.
Показательным примером сложной среды со всеми описанными нами свойствами является игра в покер [2]. В ней есть и неполнота информации о картах, и стратегии участвующих игроков, и элемент случайности, связанный с раздачей карт, и другие описанные нами трудности, возникающие во время игры. Более того, количество возможных состояний игры, характеризующих игровые ситуации, огромно.
Несмотря на кажущуюся мало применимость покерных ботов к реальным задачам, их развитие принесло множество методов, которые с карточной игры можно перенести на практику. Алгоритмы современных покерных ботов, одолевающих лучших человеческих игроков, универсальны и в целом направлены на обучение агентов в средах с неполной и асимметричной информацией [3]. Их можно перенести на множество приложений, где требуется принятие решений в аналогичной по сложности среде: от безопасности до маркетинга, в котором можно симулировать торги за аудиторию.
Исторически люди были основными участниками многоагентных ситуаций, однако c развитием ИИ появилась возможность ввести алгоритмы в повседневную жизнь как равноправных участников и агентов, с которыми можно взаимодействовать. Прямо сейчас подобные компьютерные агенты решают множество задач: от простых и безобидных как автоматические телефонные системы, до критически важных как управление безопасностью и даже управление автономным транспортом [4]. Это позволяет существенно автоматизировать многие повседневные процессы, перенося принятие решений на алгоритмы и тем самым снижая нагрузку на человека.
Особенностью многих задач, где мы применяем компьютерных агентов, является большое количество ограничений реального мира, сказывающееся на сложности их программирования [5]. А самое важное для компьютерных агентов – доступ ко всей необходимой для принятия решений информации. Игры с асимметрией и неполнотой информации требуют значительно более сложных подходов к принятию решений по сравнению с аналогичными по размерам играми с идеальной информацией, полностью доступной в любое время. Оптимальное решение в любой момент времени зависит от знания стратегии противников, зависящей от скрытой для нас и доступной только им информации, оценить которую можно только по их прошлым действия. Однако и их предыдущие действия тоже зависят от скрытой от них информации о наших действиях и того, как наши действия эту информацию раскрывали. Этот рекурсивный процесс показывает основную сложность в построении эффективных алгоритмов принятия решений.
Для проведения исследования в техасском холдеме был проведен ряд исследований для вычисления эффективности каждого алгоритма. Исследования проводились на следующих методах:
- Монте-Карло — общий игровой алгоритм, позволяющий найти лучший ход из любого игрового состояния любой игры [6].
- Q-learning - алгоритм обучения на основе политики с аппроксиматором функции в виде Q-таблицы [7].
- Deep Q-Learning —регрессионная модель, которая обычно выводит значения для каждого из наших возможных действий. Эти значения будут являться непрерывными плавающими Q-значениями [8].
- Asynchronous Advantage Actor Critic - асинхронная модель «субъект-критик»
В данной реализации будут разработаны 2 агента. Первый из них использует обычный Deep Q-Learning алгоритм, второй будет использовать Double Deep Q-Learning, их отличие заключает в том, что Double Deep Q-Learning будет использовать 2 слоя нейронной сети для обучения, что должно позволить производить более глубокое обучение сети.
В качестве платформы для проведения игр использовалась pyPockerEngine [9].
Все алгоритмы на основе нейронных сетей были разработаны с применением библиотеки TensorFlow [10].
Исследование
Для обучения было сыгранно 1000 игровых сессий по 100 раздач в каждой. Все агенты обучались параллельно, а также вместе с ними были применены 2 алгоритма без обучения со статичной стратегией. Первый всегда соглашается на повышение ставки, а второй основан на методике расчета аутов для выбора оптимальной тактики.
После обучения было проведено 100 игровых сессий со следующими условиями игры:
- Начальное число фишек: 1000;
- Малый/Большой блайнд: 1/2 фишка;
- За столом играют все алгоритмы + 2 игрока со статическим поведением;
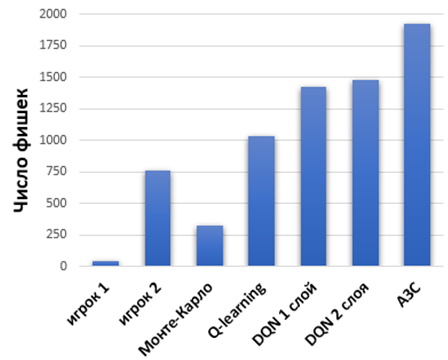
Каждый агент имел равные стартовые условия для сравнения эффективности рассматривается средний остаток фишек у игроков после 100 проведенных сессий отображенный на рисунке 1.
Рис. 1 – Результаты игры после обучения
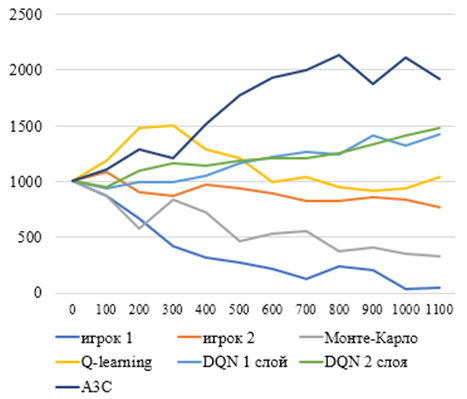
Следующим этап исследования был проанализирован весь процесс обучения с шагом в 100 партий, чтобы понять на каком этапе различные методы были более эффективны, результаты можно увидеть на рисунке 2:
Рис. 2 – Эффективность алгоритмов на разных этапах обучения
Скорость обучения не менее важный фактор при обучении агентов. Не всегда есть возможность производить обучение на мощном компьютере, но часто необходимо быстро обучаться на конкретных задачах. В данном исследовании обучение производилось на следующей конфигурации железа:
- Intel i7-3630QM 2.40 ГГц;
- Nvidia Geforce GT 640m 2 Гб;
- ОЗУ 8 Гб.
Исследование проводилось при игре каждого отдельного алгоритма с двумя статичными для того, чтобы была возможность рассчитать время для каждого агента по отдельности.
Для исследования использовался следующий объем обучения:
- 1000 игровых сессий;
- 100 игровых партий в сессии.
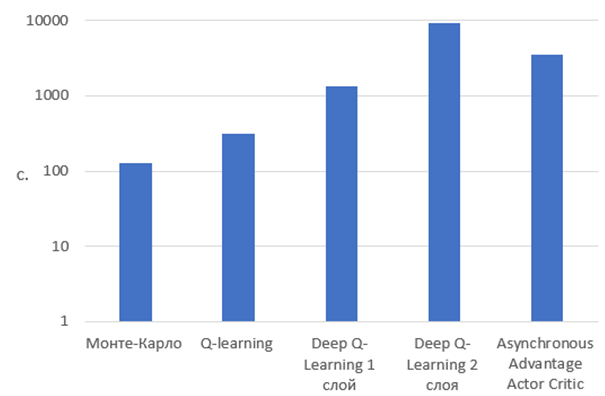
Результаты исследования представлены на рисунке 3.
Рис. 3 – Сравнение скорости обучения алгоритмов
В ходе проведенных исследований алгоритм Asynchronous Advantage Actor Critic показал лучшую способность к обучению в данной задаче, т.к. смог сохранить больше всего фишек в ходе игры в техасский холдем, но в тоже время он был одним из самых сложных в разработке и на его обучение затрачивалось больше времени чем на большинство других. Алгоритмы Монте-Карло и Q-learning оказались самыми простыми и быстрыми в обучении, но в то же время показали одни из самых низких результатов. Так как оказались не способны эффективно приспосабливаться к динамически изменяющимся условиям игры.
Алгоритм Deep Q-learning показал один из лучших результатов, но оказался очень сложным в реализации. Использование второго слоя нейронной сети не смогло показать явных преимуществ в игре техасский холдем, но сильно замедлило скорость обучения. Несмотря на это при исследовании агентов в задаче торговых ботов применение второго слоя нейронной сети показало положительное влияние на результат.
В результате было выявлено, что все алгоритмы имеют свои преимущества и недостатки и могут быть применены к многоагентным системам для решения различных задач с неполной информацией.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Russell Stuart J. Artificial Intelligence / Stuart J. Russell, Peter Norvig // A Modern Approach (Third ed.). Prentice Hall. - 2010. - P.649
- ИИ для покера: как научить алгоритмы блефовать [Электронный ресурс]. — URL: https://habr.com/ru/company/sberbank/blog/337264 (дата обращения 02.03.2018).
- Shteingart H. The role of first impression in operant learning / Shteingart, Hanan; Neiman, Tal; Loewenstein, Yonatan. // Journal of Experimental Psychology: General. 142 (2): 476–488. 2013.
- Hessel M. Rainbow: Combining Improvements in Deep Reinforcement Learning / M. Hessel, J. Modayil, H. van Hasselt et al. // ArXiv e-prints. – 2017.
- Van Hasselt H. Deep Reinforcement Learning with Double Q-learning / H. van Hasselt, A. Guez, and D. Silver. // ArXiv e-prints. 2015.
- Van Hasselt H. Learning values across many orders of magnitude / H. van Hasselt, A. Guez, M. Hessel et al. // ArXiv e-prints, 2016.
- Wang Z. Dueling Network Architectures for Deep Reinforcement Learning / Z. Wang, T. Schaul, M. Hessel et al. // ArXiv e-prints 2015.
- Silver D. Mastering the game of Go without human knowledge / D. Silver, J. Schrittwieser, K. Simonyan // USA, Nature – 2017 - P. 354–359
- PyPokerEngine [Electronic resource]. – URL: ishikota.github.io/PyPokerEngine (accessed: 29.04.2020).
- TensorFlow [Electronic resource]. – URL: https://www.tensorflow.org/ (accessed 02.03.2018).
Список литературы на английском языке / References in English
- Russell Stuart J. Artificial Intelligence / Stuart J. Russell, Peter Norvig // A Modern Approach (Third ed.). Prentice Hall. - 2010. - P.649
- II dlja pokera: kak nauchit' algoritmy blefovat' [AI for poker: how to teach algorithms to bluff] [Electronic resource]. – URL: https://habr.com/ru/company/sberbank/blog/337264 (accessed: 02.03.2020).
- Shteingart H. The role of first impression in operant learning / Shteingart, Hanan; Neiman, Tal; Loewenstein, Yonatan. // Journal of Experimental Psychology: General. 142 (2): 476–488. 2013.
- Hessel M. Rainbow: Combining Improvements in Deep Reinforcement Learning / M. Hessel, J. Modayil, H. van Hasselt et al. // ArXiv e-prints. – 2017.
- Van Hasselt H. Deep Reinforcement Learning with Double Q-learning / H. van Hasselt, A. Guez, and D. Silver. // ArXiv e-prints. 2015.
- Van Hasselt H. Learning values across many orders of magnitude / H. van Hasselt, A. Guez, M. Hessel et al. // ArXiv e-prints, 2016.
- Wang Z. Dueling Network Architectures for Deep Reinforcement Learning / Z. Wang, T. Schaul, M. Hessel et al. // ArXiv e-prints 2015.
- Silver D. Mastering the game of Go without human knowledge / D. Silver, J. Schrittwieser, K. Simonyan // USA, Nature – 2017 - P. 354–359
- PyPokerEngine [Electronic resource]. – URL: ishikota.github.io/PyPokerEngine (accessed: 29.04.2020).
- TensorFlow [Electronic resource]. – URL: https://www.tensorflow.org/ (accessed 02.03.2018).