ПОСТРОЕНИЕ ГРАФОАНАЛИТИЧЕСКИХ ОДНОЯЧЕЕЧНЫХ ПРОСТРАНСТВЕННЫХ НОМОГРАММ НИЗКОЧАСТОТНЫХ И ВЫСОКОЧАСТОТНЫХ ЗОН ПОЛОГОСТИ ВОЛНЫ
Левкин Ю.С.1, Лушкин И.А.2
1Соискатель, 2кандидат технических наук,
Тольяттинский государственный университет ТГУ
ПОСТРОЕНИЕ ГРАФОАНАЛИТИЧЕСКИХ ОДНОЯЧЕЕЧНЫХ ПРОСТРАНСТВЕННЫХ НОМОГРАММ НИЗКОЧАСТОТНЫХ И ВЫСОКОЧАСТОТНЫХ ЗОН ПОЛОГОСТИ ВОЛНЫ
Аннотация
В настоящей работе показана связь графической иллюстрации с экспериментально-расчетными её характеристиками. Отсутствие проекционной связи между плоскостями пространственной модели с геометрической ей продукцией, хоть и лишает рассматриваемую номограмму некоторых преимуществ, однако оперативность построения базовой программы MS Excel показывает связь графически и аналитики. В работе даны, физиографические и графоаналитические, анализы номографической пространственной аксонометрической модели, которая определяет физику генезиса эксперимента. Графически и аналитически описаны низкочастотная и высокочастотная зоны. Особое место в работе занимает переходная зона. Эта зона имеет аномальную характеристику точечных замеров. Графическое решение этого случая невозможно т.к. рассмотрение неразрывной струи не предполагает нарушение её структуры. Безусловно, выброс капель из области гребня в зону воздушной фазы, лишает возможности плавного перехода пологости волны, при плавном варьировании вибрационных параметров. Этот случай рассмотрен в работе при совершенно другой структуре газожидкостного вибрационного режима [8, С.39-44]. Получены эмпирические формулы, характеризующие влияние вибрационных параметров, как при низкочастотных, так и при высокочастотных колебаниях.
Ключевые слова: графоаналитическая одноячеечная пространственная номограмма, низкочастотные и высокочастотные колебания, начертательная геометрия, косая плоскость, геометрические образы, поверхность, экспериментальные и расчётные характеристики.
Levkin Yu.S.1 Lushkin I.A.2
1External Doctorate Student, 2PhD in Engineering,
Togliatti State University TSU
CONSTRUCTION OF GRAPHOANALYTICAL SINGLE-CELL SPATIAL NOMOGRAMS OF LOW-FREQUENCY AND HIGH-FREQUENCY ZONES OF WAVE FLATNESS
Abstract
In this paper, we show the relationship between a graphic illustration and its experimentally calculated characteristics. The lack of a projection relationship between the planes of the spatial model with geometric products deprives the nomogram of some advantages, but the efficiency of creating a basic MS Excel program shows a link graphically and analytically. The work contains physiographic and graphoanalytical analysis of the nomographic spatial axonometric model, which determines the physics of the genesis of the experiment. Low-frequency and high-frequency zones are graphically and analytically described. Special place in the work is given to the transition zone. This zone has an anomalous characteristic of point measurements. The graphical solution of this case is impossible as the consideration of an inseparable jet does not imply the violation of its structure. The ejection of drops from the region of the crest into the air phase zone excludes the possibility of smooth transition of wave flatness with a smooth variation of the vibration parameters. The work considers this case with a completely different structure of the gas-liquid vibration regime [8, P.39-44]. Empirical formulas characterizing the influence of vibration parameters are obtained, both for low-frequency and high-frequency oscillations.
Keywords: graphoanalytical single-column spatial nomogram, low-frequency and high-frequency oscillations, descriptive geometry, oblique plane, geometric images, surface, experimental and design characteristics.
В 1906-1908 годах впервые в Росси начал заниматься вопросами номографии Н.М. Герсеванов. Большая заслуга в деле развития теории номограмм и организации номографирования инженерных расчетов принадлежит Н.А. Глаголеву, возглавившему советскую номографическую школу [11, С. 3].
Номограммы используются в прикладных дисциплинах, таких как в медицине – номограмма для определения площади тела, в литературе акростих – номограмма, в строительстве – номограмма для определения количества автомобилей и т.д. [3, С.7].
На базе начертательной геометрии [1, С. 15], [12, С. 7], [4, С. 18], [5, С. 9] при успешном развитии современных компьютерных технологий, создалась ситуация при которой, сложные геометрические образы являются определяющим фактором оценки физической сути эксперимента. Несмотря, на отсутствие визуальной проекционной ортогональной связи между плоскостями пространственной модели с геометрической их продукцией, номограммы подобного типа могут быть востребованы при программировании.
Одним из ключевых параметров гидрогазодинамики является определение структур двухфазных потоков, в решении которых помогает одноячеечная пространственная номограмма. Вибрационное поле некоторых частот аномально негативно воздействует на структуры газожидкостных потоков. Такая зона становится аналитически не контролируемой в рамках рассматриваемой структуры. Только номографическая развёртка позволяет видеть физическую ситуацию проводимого эксперимента [8, С. 39–44].
В гидравлике открытых водоёмов, как пологость, так и обратная ей крутизна волны являются относительными величинами, которые зависят от силы ветра, фронта волны, глубины водоёма и других физических характеристик. В замкнутых гидравлических системах, нами рассматриваемых, эти величины характеризуют несколько иной физический смысл. Изучение трансформации таких параметров связано с формированием новых структур двухфазных потоков. Вибрационная длина волна (λв) это производная от частоты вибрации (fв), а вибрационные ускорение (nв) варьирует высоту волн двухфазных потоков (hв) и (hг) [6, С. 169-175.].
Для построения одноячеечной пространственной номограммы необходимо провести аналитические расчёты в программе MS Excel.
По результатам проведённого анализа экспериментальных данных табл. 1 видно, что в области частот fв = 30÷60 (Гц) числовые данные могут быть аппроксимированы семейством прямых. [14, С.113].
По той же табл. 1. области частот fв = 90÷200 (Гц) носит более сложный характер, однако закономерность прослеживается, и они могут быть рассмотрены. В указанных областях превалируют различные динамические механизмы возникновения и распространения волны.
В переходной области fв = 70÷80 (Гц) процесс образования волн происходит нестабильно, однако и такой механизм волнообразования будет оптимальным, т.к. определяется случайными факторами. Эту область из рассмотрения исключаем, т.к. течение газожидкостного потока, не имеющего структуры неразрывной струи, лишено его закономерностей.
Переходная зона fв = 70÷80 (Гц) при вибрационных ускорениях nв = 7÷5 (g) подробно описана [8, С 39–44.], где она является слабо дисперсной структурой. Аномалии, связанные с пологостью волны объясняются выбросом капель в газообразную фазу.
Таблица 1 – Зависимость влияния вибрации на пологость волны (λ/h) жидкой фазы псевдоламинарного потока. Экспериментальные данные [7, С. 107-111]
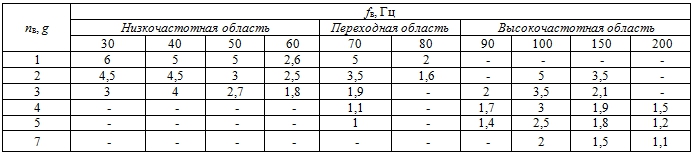
Таблица 2 – Зависимость влияния вибрации на пологость волны (λ/h) жидкой фазы псевдоламинарного потока. Результаты расчета по (89) и (25)
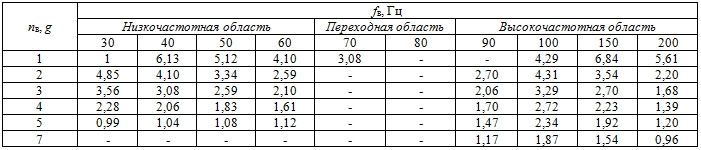
В таблицах 1 и 2 приведены результаты экспериментальных и расчётных данных [10, С. 69], на базе чего построен рис. 1 – зависимость низкочастотной области вибрации на пологость волны.
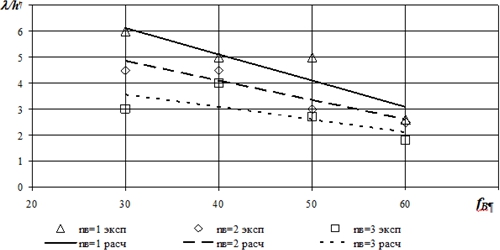
Рис. 1 – Влияние частоты вибрации fв (Гц) на пологость волны псевдоламинарного двухфазного потока. Соответствие расчета эксперименту в низкочастотной области
Физиографический анализ номограммы низкочастотных колебаний
Перед всесторонним анализом номограммы дадим характеристику её осей. Ось аппликат, как правило, является функциональной осью (λ/h), варьируемые переменные параметры, лежат на рабочей горизонтальной плоскости, с определяющими её аргументирующими осями fв (Гц) и nв (g).
- Номографическая пространственная модель (рис. 2) является графической зависимостью изменений пологости волны псевдоламинарного двухфазного потока в низкочастотной области от вибрационных параметров частоты fв (Гц) вибрации и вибрационных ускорений nв (g).
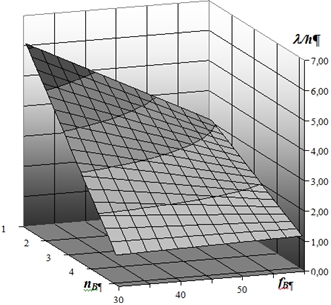
Рис. 2 – Зависимость изменений пологости волны λ/h двухфазного псевдоламинарного потока низкочастотных вибрационных параметров
- Рассматриваемая область номографической пространственной модели варьирует в диапазоне 30 ÷ 60 (Гц) на горизонтальной плоскости.
- Зависимость изменений пологости волны λ/h псевдоламинарного двухфазного потока в низкочастотной области от вибрационных параметров характеризуется плоскостью двойного параллелизма (фронтальной и профильной).
- Прямые принадлежащие плоскости и параллельные фронтальной плоскости характеризуют плоскость, как плоскость фронтального параллелизма и демонстрируют линейку данных, которая предусматривает, при постоянных вибрационных ускорениях nв (g), изменения частоты вибрации fв (Гц), каждая траектория точек прямых соответствует траекториям точек функциональным значениям пологости волны λ/h.
- Прямые принадлежащие плоскости и параллельные профильной плоскости характеризуют плоскость, как профильную плоскость параллелизма и демонстрируют линейку данных, которая предусматривает, при постоянных частотах вибрации fв (Гц), изменения вибрационных ускорений nв (g), каждая траектория точек прямой соответствует траекториям точек функциональным значениям пологости волны λ/h.
- Траектории точек кривых, равно удаленных от горизонтальной плоскости, и принадлежащие плоскости параллелизма пересекают сетку взаимно параллельных прямых, позиционируют себя как кривые уровня. На рис. 2. эти кривые показывают раздел между тонами штриховок. Каждый цвет штриховки проградуирован сеткой взаимно пересекающихся прямых, которая является ценой деления параметра λ/h.
Кривые пересекающие сетку косой плоскости, являются плоскостями уровня, которые соответствуют функциональным значениям одного аппликатного замера, а воображаемые перпендикуляры, исходящие из этих точек, проецируясь на горизонтальную плоскость показывают при каких вибрационных параметрах fв (Гц) и nв (g) возникают те или иные графические решения определения пологости волны λ/h.
Безусловно, рассматриваемый способ, не претендует на безукоризненную точность определения найденной функции. Его оценочные характеристики, при оптимально допустимой точности позволяют использование номографических иллюстраций. Произвольно взятые вибрационные параметры fв (Гц) и nв (g) на горизонтальной плоскости, при помощи восстановленного перпендикуляра, дадут встречу с косой плоскостью двойного параллелизма, однако эта встреча не может являться обязательно с плоскостью уровня. Такая ситуация требует построение, из этой точки пересечения, плоскости уровня методом интерполяции.
Графоаналитический анализ номограммы низкочастотных колебаний, в программе MS Excel
Образующие профильной плоскости параллелизма при постоянных частотах фиксируют обратно пропорциональную зависимость вибрационных ускорений от пологости волны. Образующие фронтальной плоскости параллелизма при постоянных вибрационных ускорениях направлены также обратно пропорционально пологости волн псевдоламинарного двухфазного потока.
Таблица 3 – Коэффициенты линейных уравнений
| nв (g) | А | Б |
| 1 | 9,24 | 0,102 |
| 2 | 7 | 0,075 |
| 3 | 5,08 | 0,049 |
Аппроксимация данных низкочастотной области fВ = 30÷60(Гц). Данные табл. 1. аппроксимируются удовлетворительно, прямыми линиями рис. 1. Зависимость коэффициентов табл. 3. от числа nв также хорошо описывается линейными уравнениями [14, рис. 2.6.6. и 2.6.7, С.70]. Коэффициенты (C, m, k) [14, рис. 2.6.5 – 2.6.7, С.71] хорошо описываются линейными уравнениями прямых где y – соответствующий коэффициент; х – вибрационное ускорение nв. Перейдя к экспериментальным обозначениям величин, получим эмпирическую формулу (1) определения пологости волны низкочастотной области λ/h:
![]() (1)
(1)
ІІІ. Физиографический анализ высокочастотной номограммы
Как и в предыдущем анализе, номограмма рис. 2. даёт характеристику осям рис. 3. Ось аппликат является функциональной осью (λ/h) Переменные параметры лежат, на рабочей горизонтальной плоскости, с определяющими её аргументирующими осями fв (Гц) и nв (g). Расчетные и экспериментальные кривые (рис. 3) идентичны:
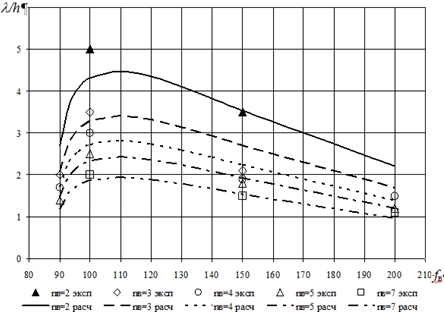
Рис. 3 – Зависимость пологости волны l/h псевдоламинарного двухфазного потока от высокочастотной вибрации
- Максимальные значения пологости волны на рис. 3. фиксируются в диапазоне fв = 100÷120 Гц.
- Увеличение частоты вибрации приводит к уменьшению пологости волн.
- Графически зоны с низко и высокочастотных колебаний выражены совершенно разными геометрическими образами (рис. 2 и 4).
- Низкочастотная область представлена косой плоскостью параллелизма. Высокочастотная область представлена поверхностью.
- Область высокочастотных колебаний рис. 4. имеет все свойства и признаки, которые имеет номограмма низкочастотных колебаний рис. 2.
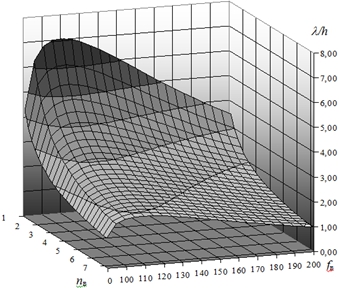
Рис. 4 – Зависимость изменений пологости волны /h псевдоламинарного двухфазного потока в высокочастотной области от вибрационных параметров fв (Гц) и nв (g) для высокочастотной области
VІ. Графоаналитический анализ номограммы высокочастотных колебаний, в программе MS Excel
Аппроксимация данных высокочастотной области fв = 90÷200 (Гц) (рис. 3), при nв = 7, 5 и 4 (g), есть максимум при fв = 100 (Гц). Подобный максимум имеется и при меньших значениях вибрационного ускорения,
В табл. 4. дана высокочастотная область. Интерполируем недостающие точки по имеющимся экспериментальным данным (интерполированные точки показаны в табл. 4. жирным).
Таблица 4 – Аппроксимация данных высокочастотной области

Перейдя к безразмерной частоте F при условии, что максимуму λ/h (fв) при fв =100 (Гц) соответствует F = 1, и добавив фиктивную точку Б пересечения с осью абсцисс получаем
![]() (3)
(3)
Наилучшее соответствие эксперименту получено при Б = 89.
Значения коэффициентов формулы (2) для каждого вибрационного ускорения представлены в табл. 5. Данные получены с использованием надстройки «Поиск решения» программы MS Excel [13, С.111-116].
Коэффициенты m и k изменяются незначительно и незакономерно, поэтому в окончательной формуле берем их средние значения.
Коэффициент С изменяется закономерно и хорошо аппроксимируется выражением.
![]() (4)
(4)
Окончательно на основании уравнений (2-4) и средних значений табл. 5, перейдя к принятым обозначениям величин, получим эмпирическую формулу (5) определения пологости волны λ/h высокочастотной области
fв = 90÷200 (Гц):
![]() (5)
(5)
Таблица 5 – Значения коэффициентов в формуле (2)

Выводы:
- Переходная зона является характерной чертой зависимости пологости волны от вибрационных параметров, в которую укладываются частоты 70÷110 (Гц). Между этими параметрами существуют совершенно разные (рис. 2 и рис. 4) зависимости, первая из которых – косая плоскость, вторая – поверхность.
- Преимущества этих моделей – всеобъемлющее решение задач, связанных с нахождением пологости, присущей тем или иным параметрам вибрации.
- Горизонтальные плоскости уровня (кривые на рис. 2), являются функциональными параметрами определения пологости волны.
Список литературы / References
- Гордон В.О. Курс начертат6ельной геометрии. [Текст] / В.О. Гордон, М.А. Семенцов – Огиевский // - М. - 1988, 2002. - С. 272.
- Грановский В.А. Методы обработки экспериментальных данных при измерениях [Текст] / В.А. Грановский. // Сирая. – Л.: Энергоатомиздат, Ленингр. отд., - 1990. – С. 288.
- Глаголев Н.А. Курс номографии учебное пособие [Текст] / Н.А Глаголев.// Высшая школа, - 2-е издание - М - 1961. - 270с.
- Климухин А.Г. Начертательная геометрия. [Текст] / А.Г Климухин. М.. - 1973. - С. 368.
- Колотов С.М. Начертательная геометрия [Текст] / С.М. Колотов, М.Ф. Вестефеев, В.Е. Мехайленко и др.// Киев: Вища школа, - 1975. - 262с.
- Левкин Ю.С. Метод определения высоты волны псевдоламинарного двухфазного потока от вибрационных воздействий [Текст]/ Ю.С. Левкин // Экология и безопасность жизнедеятельности промышленно-транспортных комплексов. - Т 4. – Тольятти, - 2011. – С. 169-175.
- Левкин Ю.С. Визуально-логическая характеристика совместного истечения жидкости и газа в трубах с поперечной вибрацией. [Текст] / Ю.С. Левкин // Известия Самарского научного центра Российской академии наук: - Специальный выпуск ”ELPIT” - Том 2. - 2005. - С107-111.
- Левкин Ю.С. Режим слабой дисперсности. [Текст] / Ю.С. Левкин // Труды ХI Международной научно-практической конференции Водоснабжение водоотведение качество и эффективность Кемерово - 2008. - С. 39–44.
- Левкин Ю.С. Некоторые структуры газожидкостных потоков в поле вибрации [Текст] /Ю.С. Левкин // - 200 экз. – Монография. – 2016. - С113.
- Левкин. Ю.С. Псевдоламинарный двухфазный режим. [Текст] / Ю.С. Левкин // - 200 экз. – Монография. – Самарский государственный авиационный университет - 2013. - С 94.
- Зуева Н.М. Номограммы МБОУ– 2013. -15с .
- Начертательная геометрия [Текст] / Четверухин Н.Ф., Левицкий В.С., Прянникова З.И., и др. М.: Высшая школа, 1963.
- Хрипунов Н.В. Применение EXCEL для обработки результатов инженерного эксперимента [Текст] / Н.В. Хрипунов, О.Я. Асанова, Е.В. Панюкова // Проведение научных исследований в области машиностроения. Сборник материалов Всероссийской научно-технической конференции с элементами научной школы для молодежи. -ТГУ- 3ч. - Тольятти - 2009 - С.111-116.
- Хрипунов Н.В. Компьютерные технологии в науке и производстве. [Текст]/ Н.В. Хрипунов, Д.И Панюков // – ТГУ, Тольятти, - 2013. – С.113.
Список литературы на английском языке / References in English
- Gordon V.O. Kurs nachertatelnoi geometrii. [Course of Descriptive Geometry.] / V.O. Gordon, M.A. Sementsov - Ogievsky // - M. - 1988, 2002. - P. 272. [In Russian]
- Granovskii V.A. Metody obrabotki eksperimentalnykh dannykh pri izmereniyakh [Methods for Processing Experimental Data in Measurements] / V.A. Granovsky. // Siraya. - L.: Energoatomizdat, Leningr. otd., - 1990. - P. 288. [In Russian]
- Glagolev N.A. Kurs nomografii. Uchebnoe posobie [Course of Nomographs. Textbook] / N.A. Glagolev.// Vysshaya Shkola, - 2nd edition - M - 1961. - 270p. [In Russian]
- Klimukhin A.G. Nachertatelnaya geometriya. [Descriptive Geometry.] / A.G. Klimukhin. M. - 1973. - P. 368. [In Russian]
- Kolotov S.M. Nachertatelnaya geometriya [Descriptive Geometry.] / S.M. Kolotov, M.F. Vestefeev, V.E. Mekhailenko and others. Kyiv: Vyshcha Shkola, - 1975. - 262p. [In Russian]
- 6 Levkin Yu.S. Metod opredeleniya vysoty volny psevdolaminarnogo dvukhfaznogo potoka ot vibratsionnykh vozdeistvii [Method for Determining the Height of a Wave of a Pseudo-Laminar Two-Phase Flow from Vibration Influences] / Yu.S. Levkin // Ecology and Life Safety of Industrial Taansport Complexes. - V. 4. - Togliatti, - 2011. - P. 169-175. [In Russian]
- Levkin Yu.S. Vizualno-logicheskaya kharakteristika sovmestnogo istecheniya zhidkosti i gaza v trubakh s poperechnoi vibratsiei. [Visually-Logical Characteristic of the Joint Outflow of Liquid and Gas in Pipes with Transverse Vibration.] / Yu.S. Levkin // News of the Samara Scientific Centre of the Russian Academy of Sciences: - Special Issue of "ELPIT" - Volume 2. - 2005. - P.107-111. [In Russian]
- Levkin Yu.S. Rezhim slaboi dispersnosti. [Mode of Weak Dispersion.] / Yu.S. Levkin // Proceedings of the XI International Scientific and Practical Conference Water Supply Water Disposal Quality and Efficiency. Kemerovo - 2008. - P. 39-44. [In Russian]
- Levkin Yu.S. Nekotorye struktury gazozhidkostnykh potokov v pole vibratsii [Some Structures of Gas-Liquid Flows in the Field of Vibration] / S. Levkin // - 200 copies. - Monograph. - 2016. - P.113. [In Russian]
- Yu.S. Psevdolaminarnyi dvukhfaznyi rezhim. [Pseudo-Laminar Two-Phase Mode.] / Yu.S. Levkin // - 200 copies. - Monograph. - Samara State Aviation University - 2013. - P. 94. [In Russian]
- Zueva N.M. Nomogrammy MBOU [Nomograms of Municipal Budget Educational Institution] – 2013. -15 p. [In Russian]
- Nachertatelnaya geometriya [Descriptive Geometry] / Chetverukhin N.F., Levitsky V.S., Spryannikova Z.I., et al. M.: Vysshaya Shkola, 1963. [In Russian]
- Khripunov N.V. Primenenie EXCEL dlia obrabotki rezultatov inzhenernogo eksperimenta [Application of EXCEL for Processing the Results of an Engineering Experiment] / N.V. Khripunov, O.Ya. Asanova, E.V. Panyukova // Conducting Scientific Research in the Field of Mechanical Engineering. Collection of Materials of the All-Russian Scientific and Technical Conference with Elements of a Scientific School for Youth. -TSU-3 p. - Togliatti - 2009 - P.111-116. [In Russian]
- Khripunov N.V. Kompiuternye tekhnologii v nauke i proizvodstve. [Computer Technologies in Science and Production.] / N.V. Khripunov, D.I. Panyukov // - TSU, Togliatti, - 2013. - P.113. [In Russian]
