ОБРАТНАЯ ЗАДАЧА О НАХОЖДЕНИИ МЕСТА СОПРЯЖЕНИЯ НЕОДНОРОДНОГО СТЕРЖНЯ
Акмадиева Т.Р.1, Захарова М.А.2, Потанина О.В.3
1Старший преподаватель, Уфимский государственный нефтяной технический университет,
2Старший преподаватель, Уфимский государственный нефтяной технический университет,
3Кандидат педагогических наук, доцент, Уфимский государственный нефтяной технический университет
ОБРАТНАЯ ЗАДАЧА О НАХОЖДЕНИИ МЕСТА СОПРЯЖЕНИЯ НЕОДНОРОДНОГО СТЕРЖНЯ
Аннотация
В работе проводится анализ статей о различных деформациях однородных стержней, а также приводятся те области науки и техники, где могут быть применены результаты исследований. Основным пунктом работы является решение новой задачи, в которой рассматривается неоднородный стержень, закрепленный на одном конце. На незакрепленный конец этого стержня действует сила нагрузки, в результате чего этот конец отклоняется. Решена задача о нахождении оптимального места сопряжения этого стержня, чтобы отклонение незакрепленного конца было наименьшим. Ранее задача о неоднородном стержне изучалась мало и результаты, полученные в работе, имеют широкое применение в промышленном производстве, строительстве, авиастроении, в нефтегазовой отрасли.
Ключевые слова: стержень, прогиб, место сопряжения, функция нагрузки, дифференциальные уравнения.
Akmadieva T.R. 1, Zakharova M.A. 2, Potanina O.V.3
1Ufa State petroleum technological University,
2Ufa State petroleum technological University,
3PhD in Pedagogy, Associate professor,
Ufa State petroleum technological University,
INVERSE PROBLEM OF FINDING CONJUNCTION PLACE OF INHOMOGENEOUS CORE
Abstract
The work analyzes a series of articles on various deformations of homogeneous cores, provides the areas of science and technology where this knowledge can be applied. The main point of the work is to solve a new problem which considers an inhomogeneous core fixed at one end. The loose end of the core is impacted by the load force which causes the deviation of the end. The problem of finding optimal location of the core conjunction in order to reduce the deviation of the loose end as much as possible has been solved. Previously, the problem of an inhomogeneous core has not been studied properly. The results provided in this work can be widely applied in industrial production, construction, aviation, oil and gas industries.
Keywords: core, deflection, conjunction place, load function, differential equations.
Чем быстрее идет вперед развитие техники, тем большие требования предъявляются к ее качеству. Перед серийным выпуском каждая новая модель тестируется на долговечность ее технических систем. При массовом производстве нельзя обнаружить неисправности в системе, прибегая к ее разборке, так как, тем самым, можно уменьшить срок ее службы. С развитием такой науки, как математическая физика, стало возможным разработать акустические методы диагностики неисправностей системы. Процессы, протекающие в механизмах, являются источниками шума. По характеру этого шума можно судить и о процессах, протекающих в любом объекте исследования. Благодаря этому возникла наука – акустическая диагностика. С помощью методов, разработанных этой наукой, обнаруживают дефекты в судовых механизмах, в авиационных и автотракторных двигателях. По звучанию шпал стало возможным устанавливать потерю контакта с насыпью, что может приводить к железнодорожной катастрофе. Исследования и решения вышеизложенных проблем были рассмотрены в работах [1, 2, 3, 4].
Еще один метод обнаружения дефектов носит название - интегральный метод свободных колебаний. Его применяют при проверке качества посуды, железнодорожных колес и других объектов, издающих характерный звон, вызываемый механическим ударом. Дефект обнаруживают в результате смещения собственной частоты звука. Но, не только по уровню звука можно определить скрытый дефект в объекте исследования.
Под воздействием внешних факторов объект может совершать колебания, по виду которых можно определить какой дефектологический процесс происходит внутри этого объекта. Возникает задача отыскания таких закреплений, которые обеспечивали бы безопасный диапазон частот колебаний. Для решения таких задач используют метод восстановления краевых условий. Эти задачи относятся к обратным задачам математической физики. Именно таким задачам посвящена наша работа. Все эти задачи являются корректно поставленными.
Задача является корректно поставленной на паре пространств S и T, если верны условия:
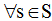 решение задачи существует;
решение задачи существует;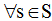 решение задачи единственно;
решение задачи единственно;- решение задачи
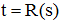 непрерывно зависит от исходных данных S, где
непрерывно зависит от исходных данных S, где 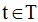 .
.
Задачи, рассмотренные в этой работе, относятся к типу граничных обратных задач. В этих задачах по значениям прогибов в нескольких точках восстанавливают краевые условия и определяют нагрузки, действующие на механическую систему. Такие задачи являются обратными задачами Ильгамова. В работе [5] был рассмотрен однородный стержень определенной длины. Под стержнем понимают одномерное упругое тело (два размера малы по сравнению с третьим), обладающее конечной жесткостью на растяжение, кручение, сжатие и изгиб. Продольные колебания такого тела описывает дифференциальное уравнение вида:
![]() .
.
Колебания изгиба этого тела описываются уравнением:
![]() ,
,
где J –момент инерции относительно оси ОУ.
Упругая опора этого стержня недоступна для визуального осмотра. По краевым условиям и условиям сопряжения в точке хС, где расположена пружина упругой опоры, была произведена диагностика всей системы. Было выявлено, что по этим условиям однозначно устанавливаются местоположение пружины и коэффициент ее жесткости. Также установлено, что достаточно знать значения прогибов в двух точках этого стержня, чтобы определить оптимальное положение этой упругой опоры. Стержни, которые рассматриваются в этих задачах, однородные.
В работе [6] также был рассмотрен однородный стержень, закрепленный на обоих концах. На него действует сила, и в двух точках расположены пружины с известной жесткостью, которые этот стержень удерживают. По этим условиям была решена задача определения коэффициентов жесткости С1, С2 и величины нагрузки, чтобы прогибы стержня были заданными величинами. Результат, полученный при решении этой задачи может быть применен в машиностроении, строительстве, проектировке нефтепроводов и газопроводов. Если в качестве стержня рассмотреть трубопровод, то можно определить величину максимального прогиба, который бы не привел к выходу из строя всей системы. Появляется возможность отслеживать местоположение дефектного участка.
Очень часто приходится сталкиваться с задачами отыскания трещины в балке. Каковы должны быть данные, чтобы решить эту задачу? В работе [7] были определены эти условия. Зная величины прогибов балки в двух точках слева и справа от возможного места дефекта можно определить величину этой трещины С.
К причинам, приводящим к выходу из строя механической системы относятся изгиб и кручение отдельных частей этой системы. Если отождествить элемент, подвергающийся этим воздействиям со стержнем, можно рассмотреть задачу о продольно-поперечном изгибе стержня. В работе [8] эта задача была решена. Формулы, полученные в этой работе, позволяют диагностировать интенсивность поперечных нагрузок и надежность закрепления балок по значениям их прогибов в доступных для осмотра местах. Результаты применяются в строительстве. По ним можно определить возможность обрушения конструкции. Во всех рассмотренных задачах [9, 10, 11, 12, 13, 14] мы имеем дело с однородными стержнями.
Особый интерес представляют обратные задачи для определения места сопряжения и функции нагрузки для неоднородных стержней. Такой тип задач мало изучен, поэтому представляет интерес для исследования. В данной работе рассмотрим такую задачу.
Дан неоднородный стержень, жестко закрепленный на левом конце. На стержень действуют нагрузки у1 и у2, под действием которых правый конец стержня отклоняется на заданную величину. Требуется найти оптимальное место сопряжения этого стержня, чтобы величина отклонения незакрепленного конца была наименьшей. Данная задача ранее не рассматривалась.
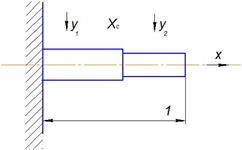
Рис. 1 - Закрепленный стержень без воздействия нагрузки
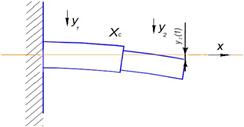
Рис. 2 - Закрепленный стержень под воздействием нагрузки
Для стержня длины l заданы характеристики: B, H, - размеры сечения закрепленного конца стержня, b, h - размеры сечения свободного (незакрепленного) конца стержня и моменты инерции ![]() .
.
Даны краевые условия 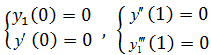
и условия сопряжения 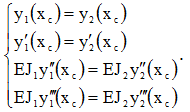 .
.
Решим сначала прямую задачу.
Пусть известны все характеристики стержня ![]() , а также место сопряжения хС, где q1 - полином, выражающий интенсивность распределенной нагрузки на одной части стержня, q2 - полином, выражающий интенсивность нагрузки на другой его части , E – модуль упругости Юнга, J – момент инерции относительно оси изгиба. По этим условиям нужно найти функцию отклонения правого конца этого стержня.
, а также место сопряжения хС, где q1 - полином, выражающий интенсивность распределенной нагрузки на одной части стержня, q2 - полином, выражающий интенсивность нагрузки на другой его части , E – модуль упругости Юнга, J – момент инерции относительно оси изгиба. По этим условиям нужно найти функцию отклонения правого конца этого стержня.
Пусть ![]() , где
, где ![]() .
.
Имеем систему дифференциальных уравнений четвертого порядка 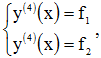 ,
,
общее решение которой задается системой
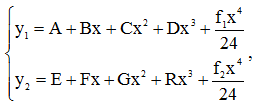
где A, B, C, D, E, F, G, R - неизвестные числовые коэффициенты.
Рассмотрим начальные условия 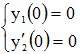 . Исходя из краевых условий, следует, что
. Исходя из краевых условий, следует, что 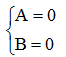 и, значит,
и, значит, ![]() . Аналогично
. Аналогично 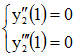 . Так как
. Так как 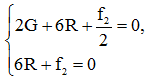 то
то 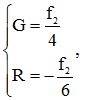 откуда получим
откуда получим
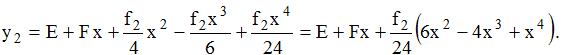 .
.
Рассмотрим условия сопряжения в точке ![]() :
:
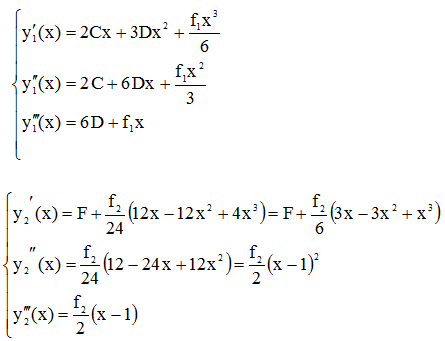
Получим систему уравнений для определения числовых коэффициентов C, D, E, F. Подставим в первое уравнение условий сопряжения ![]()
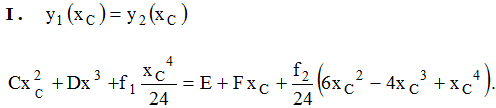
Аналогично, подставим данные в оставшиеся условия.
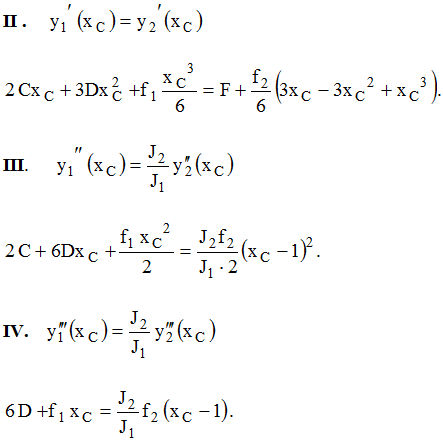
Из IV имеем
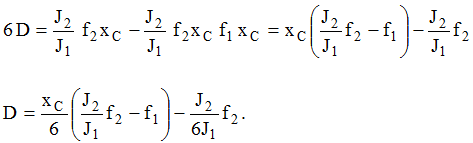
Из III имеем
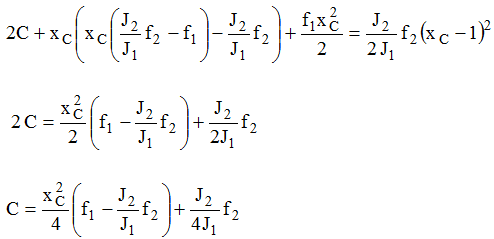
Из II
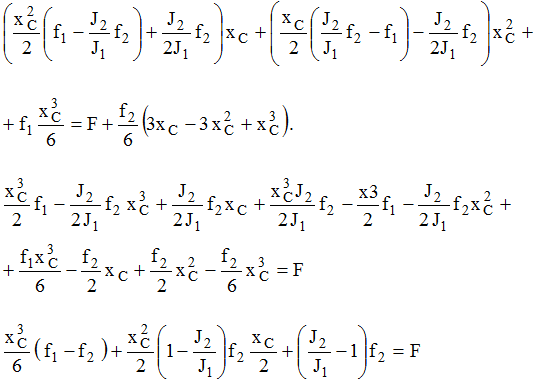
Подставим в I
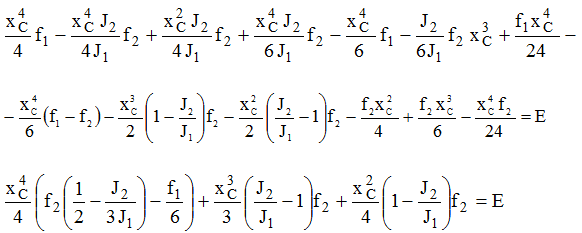
Таким образом, получим выражения, позволяющие определить функции прогибов.
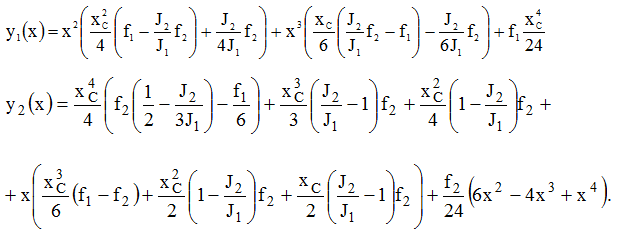
С учетом краевых условий получим значение функции прогиба на правом конце стержня:
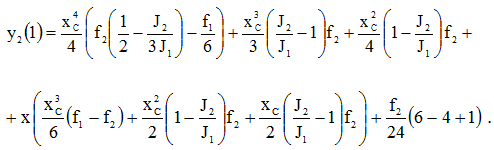
Дальнейшие преобразования этого выражения позволяют определить окончательный вид функции прогиба у2(1).
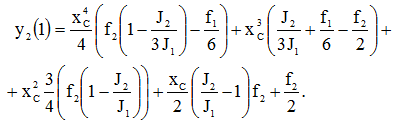
Исходя из полученной формулы видно, что значение прогиба правого конца зависит только от места сопряжения xC и значений нагрузок f1 и f2, зная которые определяется величина у2(х). Значит, зная величину прогиба и значения функций нагрузки f1 и f2 можно определить место сопряжения, то есть решить обратную задачу.
Рассмотрим задачу на конкретном примере. Расчеты проведем в безразмерных единицах.
Пусть 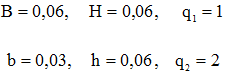
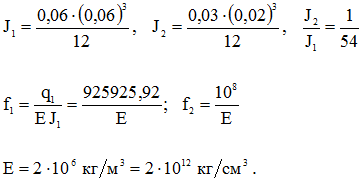
Пусть ![]()
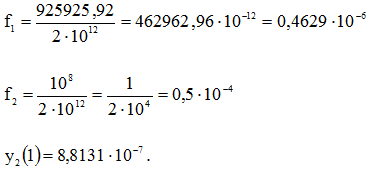
Прямая задача решена. Решим обратную задачу. Известна величина прогиба у2(1) правого конца стержня. Необходимо определить место сопряжения хС.
Пусть ![]()
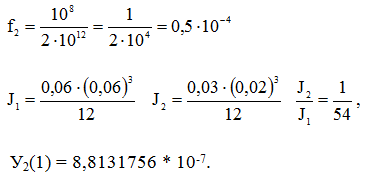
Решив уравнение четвертой степени относительно неизвестной xC, получили xC = 0,1, единственный корень, который удовлетворяет условию ![]() .
.
Результаты, полученные при решении этой задачи могут быть применены в строительстве, машиностроении, нефтегазовой отрасли. Зная место сопряжения, можно будет оптимизировать отклонение незакрепленного конца балки , что не будет приводить к деформации объектов. Важность рассмотрения задач диагностики систем выходят на первый план в связи с увеличением техногенных катастроф и опасностями, связанными с изношенностью основных частей механизмов. Методы обнаружения трещин, определения форм и размеров дефектов достаточно хорошо разработаны. Большое значение уделяется разработкам методов виброзащиты. Колебания систем или их отдельных частей приводят к некомфортным условиям работы, а в некоторых случаях эти колебания находятся в опасном для здоровья диапазоне. Поэтому задача отыскания таких закреплений системы , которые обеспечивали бы безопасный диапазон частот выходят на первый план. По этой причине результаты, полученные в ходе решения задачи о неоднородном стержне имеют большое практическое значение и актуальны в настоящее время.
Список литературы / References
- Кузьмин Р.В. Дифектация судовых механизмов. / Кузьмин Р.В. – М.: Транспорт.1967. – 174 с.
- Бухтияров И.Д. Исследования по акустической диагностике цилиндро-поршневой системе ДВС / Бухтияров И.Д. , Аллилуев В.А. // Труды СибВИМа. – Новосибирск, 1968. – Вып.4. – С. 378-879.
- Диагностика автотракторных двигателей / Под ред. Н.С.Ждановского. – Л.: Колос, 1977. – 264 с.
- Васильев Н.А. Экспериментальные исследования колебательных характеристик железнодорожных шпал / Васильев Н.А., Дворников С.И. // Акустический журнал. – 2000. – Т.46, №3. – С. 424-426.
- Захарова М.А. Статическая задача определения нагрузки, действующей на стержень и жесткости его упругой опоры. / Захарова М.А. // Академический журнал Западной Сибири. – 2010. - №2. – С.50-52.
- Ахтямов А.М. Обратная задача об определении условий сопряжений и величин постоянной нагрузки, действующих на стержень / Ахтямов А.М., Захарова М.А. // В мире научных открытий. - 2010. - № 4-13. - С. 142-145.
- Захарова М.А. Определение коэффициентов жесткости пружины при продольно-поперечном изгибе стрежня / Захарова М.А., Ахтямов М.А. // В сборнике: Математическое и компьютерное моделирование естественнонаучных и социальных проблем. //V Международная научно-техническая конференция молодых специалистов, аспирантов и студентов. - 2011. - С.65-68
- Ахтямов А.М. Обратная задача для продольно-поперечного изгиба стержня / Ахтямов А.М., Захарова М.А. // Строительная механика инженерных конструкций и сооружений. - - № 4. - С. 31-33.
- Акмадиева Т.Р. Статическая задача об определении величины постоянной нагрузки, действующей на балку, и величины коэффициента С, характеризующего дефект балки / Акмадиева Т.Р., Захарова М.А. // В мире научных открытий . - 2015. - №12.1(72). - С.351-355.
- Ахтямов А.М. Идентификация местоположения и коэффициента жесткости пружины упругой опоры стержня / Ахтямов А.М., Захарова М.А. // В сборнике: Математическое моделирование и краевые задачи. // Труды седьмой Всероссийской научной конференции с международным участием. - - С. 42-44.
- Ахтямов А.М. Статическая задача об определении величины постоянной нагрузки, действующей на балку, и величины коэффициента С, характеризующего дефект балки / Ахтямов А.М., Захарова М.А. // Обозрение прикладной и промышленной математики. - 2010. - Т. 17. № 6. - С. 838.
- Ахтямов А.М. Обратная задача об установлении параметра дефекта жесткой балки / Ахтямов А.М., Захарова М.А. // В книге: Фундаментальная математика и ее приложения в естествознании. // Тезисы докладов Международной школы – конференции для студентов, аспирантов и молодых ученых. - - С. 11.
- Захарова М.А. Статическая задача определения нагрузки, действующей на стержень и жесткости его упругой опоры / Захарова М.А. // Академический журнал Западной Сибири. - 2010. - № 2. - С. 50-52.
- Ахтямов А.М. Обратная задача об определении условий сопряжения и величины постоянной нагрузки, действующей на стержень / Ахтямов А.М. , Захарова М.А. // В книге: Фундаментальная математика и ее приложения в естествознании. // Тезисы докладов Международной школы – конференции для студентов, аспирантов и молодых ученых. - - С. 33.
Список литературы на английском языке / References in English
- Kuz'min R.V. Difektacija sudovyh mehanizmov [Defectate ship machinery] / Kuz'min R.V. – M.: Transport.1967. – 174 р. [in Russian]
- Buhtijarov I.D. Issledovanija po akusticheskoj diagnostike cilindro-porshnevoj sisteme DVS [Research on acoustic diagnostics of cylinder-piston system of internal combustion engines / Buhtijarov I.D. , Alliluev V.A. // Trudy [Proceedings] SibVIMa. – Novosibirsk, 1968. – V.4. [ release 4] – Р. 378-879. [in Russian]
- Diagnostika avtotraktornyh dvigatelej [Diagnosis of automotive engines] / Pod red. N.S.Zhdanovskogo. – L.: Kolos, 1977. – 264 р. [in Russian]
- Vasil'ev N.A. Jeksperimental'nye issledovanija kolebatel'nyh harakteristik zheleznodorozhnyh shpal [Experimental study of the vibrational characteristics of railway sleepers] / Vasil'ev N.A., Dvornikov S.I. / / Akusticheskij zhurnal [Acoustic journal] – 2000. – T.46, №3. – р. 424-426. [in Russian]
- Zaharova M.A. Staticheskaja zadacha opredelenija nagruzki, dejstvujushhej na sterzhen' i zhestkosti ego uprugoj opory. [The static problem of determining the load acting on the rod and of stiffness of the elastic support] / Zaharova M.A. // Akademicheskij zhurnal Zapadnoj Sibiri. [Academic journal of Western Siberia] – 2010. - №2. – Р.50-52. [in Russian]
- Ahtjamov A.M., Obratnaja zadacha ob opredelenii uslovij soprjazhenij i velichin postojannoj nagruzki, dejstvujushhih na sterzhen'. [The inverse problem concerning the determination of the terms of the mates and the values of the permanent load acting on the rod] / Ahtjamov A.M., Zaharova M.A. // V mire nauchnyh otkrytij [In the world of scientific discovery] - 2010. - № 4-13. - Р. 142-145. [in Russian]
- Zaharova M.A. Opredelenie kojefficientov zhestkosti pruzhiny pri prodol'no-poperechnom izgibe strezhnja . [Determination of the stiffness of the spring in longitudinal-transverse bending of the rod] / Zaharova M.A., Ahtjamov M.A. // V sbornike: Matematicheskoe i komp'juternoe modelirovanie estestvennonauchnyh i social'nyh problem. [In the book: Mathematical and computer modeling of natural-science and social problems] // V Mezhdunarodnaja nauchno-tehnicheskaja konferencija molodyh specialistov, aspirantov i studentov. [V international scientific-technical conference of young specialists, postgraduates and students] - 2011. - Р.65-68 [in Russian]
- Ahtjamov A.M. Obratnaja zadacha dlja prodol'no-poperechnogo izgiba sterzhnja. [The inverse problem for the longitudinal-transverse bending of the rod] / Ahtjamov A.M., Zaharova M.A. // Stroitel'naja mehanika inzhenernyh konstrukcij i sooruzhenij [Structural mechanics of engineering constructions and buildings] - 2011. - № 4. - Р. 31-33. [in Russian]
- Akmadieva T.R. Staticheskaja zadacha ob opredelenii velichiny postojannoj nagruzki, dejstvujushhej na balku, i velichiny kojefficienta S, harakterizujushhego defekt balki. [The static problem of determining the value of the permanent load acting on the beam, and the magnitude of the coefficient C, characterizing the defect beams] / Akmadieva T.R., Zaharova M.A. // V mire nauchnyh otkrytij [In the world of scientific discovery] - 2015. - №12.1(72). - Р.351-355. [in Russian]
- Ahtjamov A.M. Identifikacija mestopolozhenija i kojefficienta zhestkosti pruzhiny uprugoj opory sterzhnja. [Identification of the location and the stiffness coefficient of the spring elastic support of the rod] / Ahtjamov A.M., Zaharova M.A. // V sbornike: Matematicheskoe modelirovanie i kraevye zadachi. [In the book: Mathematical modeling and boundary problems] // Trudy sed'moj Vserossijskoj nauchnoj konferencii s mezhdunarodnym uchastiem. [Proceedings of the seventh Russian scientific conference with international participation] - 2010. - Р. 42-44. [in Russian]
- Ahtjamov A.M. Staticheskaja zadacha ob opredelenii velichiny postojannoj nagruzki, dejstvujushhej na balku, i velichiny kojefficienta S, harakterizujushhego defekt balki. [The static problem of determining the value of the permanent load acting on the beam, and the magnitude of the coefficient C, characterizing the defect beams / Ahtjamov A.M., Zaharova M.A. // Obozrenie prikladnoj i promyshlennoj matematiki. [Review of applied and industrial mathematics] - 2010. - T. 17. № 6. - Р. 838. [in Russian]
- Ahtjamov A.M. Obratnaja zadacha ob ustanovlenii parametra defekta zhestkoj balki. [Inverse problem of finding parameter of the defect rigid beam] / Ahtjamov A.M., Zaharova M.A. // V knige: Fundamental'naja matematika i ee prilozhenija v estestvoznanii. [In the book: Fundamental mathematics and its applications in the natural Sciences] // Tezisy dokladov Mezhdunarodnoj shkoly – konferencii dlja studentov, aspirantov i molodyh uchenyh. [Abstracts of the International school – conference for students, postgraduates and young scientists] - 2010. - Р. 11. [in Russian]
- Zaharova M.A. Staticheskaja zadacha opredelenija nagruzki, dejstvujushhej na sterzhen' i zhestkosti ego uprugoj opory. [The static problem of determining the load acting on the rod and of stiffness of the elastic support] / Zaharova M.A. // Akademicheskij zhurnal Zapadnoj Sibiri. [Academic journal of West Siberia] - 2010. - № 2. - Р. 50-52. [in Russian]
- Ahtjamov A.M. Obratnaja zadacha ob opredelenii uslovij soprjazhenija i velichiny postojannoj nagruzki, dejstvujushhej na sterzhen'. [The inverse problem concerning the determination of the conditions of conjugation and magnitude of the permanent load acting on the rod] / Ahtjamov A.M., Zaharova M.A. // V knige: Fundamental'naja matematika i ee prilozhenija v estestvoznanii [In the book: Fundamental mathematics and its applications in the natural Sciences] // Tezisy dokladov Mezhdunarodnoj shkoly – konferencii dlja studentov, aspirantov i molodyh uchenyh. [ Abstracts of the International school – conference for students, postgraduates and young scientists] - 2009. - Р. 33. [in Russian]
