ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ ТЕОРИИ ВОЗВРАТОВ ПУАНКАРЕ С ИСПОЛЬЗОВАНИЕМ ОТОБРАЖЕНИЙ АРНОЛЬДА
ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ ТЕОРИИ ВОЗВРАТОВ ПУАНКАРЕ С ИСПОЛЬЗОВАНИЕМ ОТОБРАЖЕНИЙ АРНОЛЬДА
Научная статья
Ильичев В.Ю.*
ORCID: 0000-0003-1017-5544,
Калужский филиал Московского государственного технического университета имени Н.Э. Баумана, Калуга, Россия
* Корреспондирующий автор (patrol8[at]yandex.ru)
АннотацияЦелью работы является разработка программы для реализации классического и модифицированного методов отображений Арнольда, позволяющей исследовать влияние начальных параметров отображений на факт возникновения или отсутствия возвратов, трактуемых соответствующей теоремой Пуанкаре.
Программа предназначена для работы с изображениями, поэтому для создания её кода выбран язык Python с подключением дополнительных модулей, хорошо зарекомендовавший себя при проведении предыдущих исследований автора и демонстрирующий удобство обработки матриц, сформированных из пикселей изображений.
Приводятся результаты, полученные с использованием разработанной программы; выработаны рекомендации по сферам применения рассмотренных алгоритмов обработки изображений. Созданная программа выложена в свободном доступе на сайте автора.
Ключевые слова: возвраты Пуанкаре, отображение Арнольда, синергетика, топология, язык Python, модуль Numpy, теория хаоса.
NUMERICAL IMPLEMENTATION OF POINCARÉ RECURRENCE THEORY USING ARNOLD MAPPINGS
Research article
Ilyichev V.Yu.*
ORCID: 0000-0003-1017-5544,
Kaluga Branch of Bauman Moscow State Technical University, Kaluga, Russia
* Corresponding author (patrol8[at]yandex.ru)
AbstractThe purpose of the work is to develop a program for implementing classical and modified Arnold mapping methods, which allows to investigate the effect of initial mapping parameters on the fact of the occurrence or absence of returns interpreted by the corresponding Poincaré theorem.
The program is designed to work with images, so to create its code, the Python language is chosen with the connection of additional modules, which has proven itself in previous studies of the author and demonstrates the convenience of processing matrices formed from image pixels.
The results obtained using the developed program are presented; recommendations were made on the scope of application of the considered image processing algorithms. The created program is freely available on the author's website.
Keywords: Poincaré returns, Arnold mapping, synergy, topology, Python language, Numpy module, chaos theory.
IntroductionOne of the most promising and rapidly developing fields of science is synergetics [1], which aims to find an explanation for the phenomena of the self-organization of systems in conditions of seeming chaos. Despite the fact that such phenomena are observed in a huge number of processes of the surrounding reality, from a mathematical and physical point of view they began to be seriously considered only over the past two centuries (earlier this sphere belonged to philosophical and theosophical issues). Scientific and technological progress has now come to a point when it is impossible to investigate the behavior of many complex systems without attracting synergetics. In this regard, many hypotheses and theories appear that consider processes in the complex and form a close connection of sciences (in particular, physics, mathematics, biology, sociology, philosophy). The time has come to unite many scientific industries based on the knowledge of the new universal laws. At the same time, the laws and dependencies already used are not rejected, but there is an understanding of the limited conditions in which they can be applied.
Synergetics uses the principles of topology [2], which considers from the point of view of mathematics the conditions for the transition of systems from one external form to another. One of the greatest scientists, the ancestor of topology, is Henri Poincaré.
This work is a contribution to the study of problems that are the subject of synergetics and computational topology, and are within the scope of scientific interests of the author [3]. Within its framework, it is necessary to develop a tool for studying some laws of Poincaré recurrence theory [4]. This theory states that with some transformations of systems, almost any phase trajectory emanating from a given starting point will pass an infinite number of times in a close neighborhood of the original state.
It should be noted that the returnability of systems in general is one of the main ideas of modern science. The study of such returns allows not only a better understanding of the laws of nature, but also a more accurate prediction of the behavior of complex systems of various kinds (which are currently based on statistics).
For a visual demonstration of this theory (but not to prove it), the so-called Arnold mapping [5] in some cases can be successfully used - a mathematical description of such a transformation of the coordinates of the points of an object, in which for a number of recounts visible chaos of the system forms, but as a result the system returns to its original state. This mapping is a special case of the Poincaré described homeomorphism (continuous mapping of topological spaces), which is a hyperbolic mapping of the torus [6].
Thus, the goal of the work was formulated - the creation of program code that implements different types of Arnold mapping in application to the processing of image files, and the study of the effect of the initial parameters of the mathematical model on the course and result of the mapping, on the possibility and speed of returning to the original image.
MethodsTwo Arnold mapping methods are considered, suitable for images having equal dimension (resolution, number of pixels) along the x and y coordinate axes:
- classical, in which at each iteration of calculations, the transformation of the coordinates of image pixels (and in the general case, the coordinates of any numerical data forming a matrix) is carried out according to the formulas:
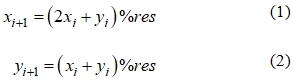
where xi and yi, xi+1 and yi+1 are pixel coordinates on the i-th and (i+1)-th iterations;
% res is the remainder of the integer division by the image resolution value.
- modified, in which conversion is carried out according to the formulas:
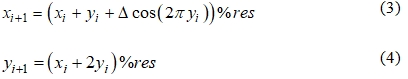
To use the above transformations, a program in the Python programming language [7] was compiled and posted for free use on the author's website [8]. The program consists of the following units:
- Importing Matplotlib library functions [9] to generate an array of pixel values from the original image, a Numpy module for processing arrays, and a Math module for using mathematical functions found in equations (1-4).
- Assigning values to the original parameters (Δ, total number of iterations t and respectively intermediate generated images, image resolution).
- Reading an image file and converting it to an array of pixel values.
- Creating arrays to fill with pixel coordinates (before iteration xi and yi, and after iteration xi+1 and yi+1). In the case of obtaining a non-integer coordinate value (which is possible, for example, when calculating by formula (3) at some Δ or due to accumulation of calculation error), the fractional part is discarded when generating the pixel coordinate of the image (but in further calculations a full value is used, without discarding the fractional part).
- Organizing a transformation cycle that is executed a specified number of times t. After each iteration, the Matplotlib function converts the new pixel matrix to an image file whose name displays the iteration number. Thus, by viewing the received images, you can see the result of each iteration.
Results
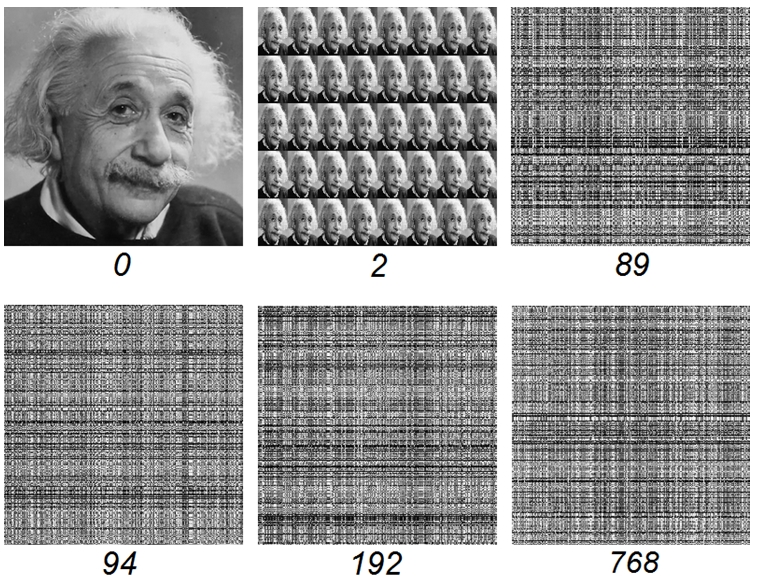
For the numerical experiment, an image file with a resolution of 256x256 pixels was selected. This image, as well as the graphics obtained after some iterations using the classic Arnold mapping, are given in Figure 1.

Fig. 1 – Source and intermediate images generated by the program with iteration numbers
Based on the presented results, it can be concluded that the classical Arnold mapping in the case of working with the 256x256 array leads to the return after 192 iterations. Intermediate iterations visually demonstrate a different measure of chaos. In most of them, the original appearance of the image cannot be recognized in any way. From this we can draw the practical conclusion that the above conversion can be successfully used to encrypt image files or other data arrays [10]. The results of using the modified mapping are highly dependent on the parameter Δ included in formulas (3, 4). Numerous calculations using the program (up to 50 thousand iterations for each Δ) showed the following:- with Δ equal to 0 and other integers, results identical to the classical transformation are obtained.
- values increases the number of iterations required to receive a return to 768. The intermediate results of the transformations are very similar to those formed at Δ=0.
- with other values of Δ, it was not possible to achieve a return to the original image even in 50 thousand iterations. All intermediate results, except the very first iterations, almost identical in structure. Figure 2 shows for example the results of iterations at Δ=0.33.
Fig. 2 – Results of iterations in implementation of modified Arnold mapping and intermediate values of Δ
- Calculation is carried out at random (but varying in the range from 0 to 1 and multiples of 0.1) values of Δ, changing at each iteration. As expected, no return occurred to the original image. Therefore, this case is not suitable for the visual demonstration of Poincaré returns.
- For processing, png files with compression were used, so the volume of image files containing ordered images (such as iterations 0, 2, 94, 192 in Figure 1) is tens or even hundreds of times smaller than image files perceived as noise (iterations 89, 94, 192, 768 in Figure 2, forming png files of approximately equal size).
Discussion
From the results obtained, it can be concluded that Poincaré returns are fully performed when implementing the classic Arnold mapping algorithm. For a modified mapping, returns are not performed with all initial values of variables - perhaps they would be possible with more iterations than 50 thousand, but to prove this it will require the creation of a special program and very long calculations. At the described stage of research, such a task was not set.
The second conclusion is that when performing the classical mapping algorithm, the number of iterations to achieve a return of the image to the original view is not a smooth function of the resolution of the image used (Figure 3).
Fig. 3 – The number of iterations required to return to the original image depends on the resolution of the image.
Since the resolution values were chosen, multiples of 50 (which, moreover, are even numbers), for the final conclusion of the revealed pattern, it is also necessary to carry out a "through" calculation at all intermediate resolution values. The developed program allows to perform such a calculation, but it is extremely labor-intensive. However, even for selected discrete resolution levels, you can see that the number of iterations required for return increases on average with increasing image resolution (in Figure 3, a linear trend line is built for this).
In general, the image transformation considered can be characterized simultaneously as having both chaotic and logical (returnability) properties, which is just characteristic of the behavior of many complex systems and forms the basis of chaos theory.
Conclusion
As a result of the work, the following tasks were solved:
- some of the questions posed to the new science - synergetics - are described and specific goals achieved in the course of the ongoing research are highlighted;
- an algorithm and program code in Python were compiled to demonstrate Poincaré recurrence theory using Arnold mapping methods by processing image files;
- results showing the work of the program and the features of the two mapping methods;
- conclusions were drawn on the prospects of using the developed program for further research.
The created program can also be used to teach the basics of synergetics, chaos theory, topology, to prepare presentations and further improve image transformation processes using additional Python language modules.
| Благодарности Благодарю коллектив редакции. | Acknowledgement Thanks to the editorial staff. |
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Negmatov I. Sinergetics as a new methodological direction in modern times / I. Negmatov // Test Engineering and Management. - 2020. - Vol. 83. - № 5-6. - P. 1798-1802.
- Porter J.E. 50th spring topology and dynamical systems conference contributed problems in set-theoretic topology / J.E. Porter // Topology Proceedings. - 2017. - P. 351-368.
- Ilichev V.Y. Development of program for determination of fractal dimensions of images / V.Y. Ilichev // International Research Journal. - 2021. - № 4-1 (106). - P. 6-10.
- Anishchenko V.S. Poincaré recurrence theory and its applications to nonlinear physics / V.S. Anishchenko, S.V. Astakhov // Physics-Uspekhi. - 2013. - Vol. 56. - № 10. - P. 955-972.
- Hasegawa H.H. Spectral decomposition of the stretching dynamics of the Arnold cat map / H.H. Hasegawa, D.J. Driebe, C.B. Li // Physics Letters A. - 2003. - Vol. 319. - № 3-4. - P. 290-298.
- Banakh T.O. Ergodic deformations of nonlinear Hamilton systems and local homeomorphism of metric spaces / T.O. Banakh, A.K. Prykarpatsky // Journal of Mathematical Sciences. - 2019. - Vol. 241. - № 1. - P. 27-35.
- Prokopiev M.S. Development of a programming course for students of a teacher training higher education institution using the programming language Python / M.S. Prokopiev, E.Z. Vlasova, T.V. Tretyakova et al. // Propositos y representaciones. - 2020. - Vol. 8. - № 3. - P. 15.
- Program for demonstration Poincaré recurrence theory using Arnold mappings. [Electronic resource] URL: http://turbopython.ru/poincare (accessed 04.05.2021).
- Ilichev V.Yu. Development of procedure for determination of characteristics of heated polycarbonate greenhouses / V.Yu. Ilichev // International Research Journal. - 2021. - № 2-1 (104). - P. 132-135.
- Minati Mishra. High security image steganography with modified Arnold cat map / Minati Mishra, Ashanta Ranjan Routray, Sunit Kumar. // International Journal of Computer Applications. - 2012. – V. 37. - № 9. – P. 16-20.