МЕТОДИКА ОПРЕДЕЛЕНИЯ СУММАРНОЙ ДЛИНЫ ВЕРТИКАЛЬНЫХ СКВАЖИН ДЛЯ ГЕОТЕРМАЛЬНЫХ ТЕПЛОВЫХ НАСОСОВ
МЕТОДИКА ОПРЕДЕЛЕНИЯ СУММАРНОЙ ДЛИНЫ ВЕРТИКАЛЬНЫХ СКВАЖИН ДЛЯ ГЕОТЕРМАЛЬНЫХ ТЕПЛОВЫХ НАСОСОВ
Научная статья
Псаров С.А.1, *, Шумилин Е.В.2, Каменчуков А.В.3
1 ORCID: 0000-0002-4368-7848;
2 ORCID: 0000-0002-3210-1469;
3 ORCID: 0000-0001-7997-3195;
1, 2, 3 Тихоокеанский государственный университет, Хабаровск, Россия
* Корреспондирующий автор (006212[at]pnu.edu.ru)
АннотацияВ работе предложена методика определения требуемой длины геотермальных скважин для тепловых насосов типа «грунт» − «вода» на основе трех составляющих: среднегодового потребления тепловой мощности, среднемесячного потребления тепловой мощности в наиболее холодный месяц и пикового потребления тепловой мощности в расчетный период (например, наиболее холодную пятидневку с обеспеченностью 0,92). Проведено моделирование работы теплового насоса и поля геотермальных скважин для среднемесячных климатических условий г. Хабаровска для одноэтажного жилого дома площадью 105 м2. Показано, что в климатических условиях г. Хабаровска треть скважин необходимы для обеспечения безаварийной работы теплового насоса в течение многолетнего периода, треть скважин необходимы для обеспечения работы насоса в наиболее холодный месяц и треть скважин необходимы для обеспечения пиковых нагрузок в течение наиболее холодной пятидневки. Предложенная методика позволяет провести анализ составляющих требуемой суммарной длины скважин с целью ее уменьшения, что приводит к уменьшению стоимости обустройства теплоснабжения на базе геотермальных тепловых насосов и увеличению их экономической привлекательности.
Ключевые слова: геотермальный тепловой насос, геотермальная скважина, термическое сопротивление геотермальной скважины, g-функция.
METHOD FOR DETERMINING THE TOTAL LENGTH OF VERTICAL WELLS FOR GEOTHERMAL HEAT PUMPS
Research article
Psarov S.A.1, *, Shumilin E.V.2, Kamenchukov A.B.3
1 ORCID: 0000-0002-4368-7848;
2 ORCID: 0000-0002-3210-1469;
3 ORCID: 0000-0001-7997-3195;
1, 2, 3 Pacific National University, Khabarovsk, Russia
* Corresponding author (006212[at]pnu.edu.ru)
AbstractThe study proposes a method for determining the required length of geothermal wells for the soil-water heat pumps on the basis of three components: the average annual heat power consumption, the average monthly heat power consumption in the coldest month, and the peak heat power consumption in the calculation period (for example, the coldest five-day period with a supply of 0.92). The research includes a simulation of the heat pump and geothermal field operation for the average monthly climatic conditions of Khabarovsk for a one-story residential building with an area of 105 m2. The study illustrates that in the climatic conditions of Khabarovsk, a third of wells are necessary to ensure a trouble-free operation of the heat pump over a multi-year period, a third of wells are necessary to ensure pump operation in the coldest month, and a third of wells are necessary to ensure peak loads during the coldest five-day period. The proposed method makes it possible to analyze the components of the required total length of wells in order to reduce it, which leads to a reduction in the cost of arranging heat supply based on geothermal heat pumps and an increase in their economic attractiveness.
Keywords: geothermal heat pump, geothermal well, geothermal well thermal resistance, g-function.
ВведениеДля работы теплового насоса необходим энергоемкий источник низкопотенциальной теплоты естественного или искусственного происхождения. К таким источникам можно отнести наружный воздух, грунт, подземные или поверхностные воды, сбросные воды, удаляемый воздух систем вентиляции и другие. Наибольшее распространение получили тепловые насосы, использующие в качестве источника теплоты наружный воздух («воздух» - «вода» или «воздух» - «воздух») или грунт («грунт» - «вода» с вертикальными скважинами) [1]. Это связано с относительной доступностью данных источников теплоты и отсутствием проблем с выполнением законов о защите земных недр при обустройстве геотермальных скважин до первого водного горизонта (до 30 ÷ 50 метров). Горизонтальные геотермальные контуры для тепловых насосов «грунт» - «вода» получили меньшее распространение из-за большого объема земляных работ [2]. Следует отметить, что оба типа тепловых насосов: «воздух» - «вода» и «грунт» - «вода» имеют свои преимущества и недостатки, поэтому сделать однозначный выбор между ними невозможно.
Например, у воздушных тепловых насосов при температурах наружного воздуха ниже минус 15 оС существенно уменьшаются коэффициент трансформации теплоты и мощность. А тепловые насосы, получающие тепловую энергию из грунта, могут работать в узком диапазоне температур от минус 3 до плюс 8 оС. Поэтому все элементы системы теплоснабжения и горячего водоснабжения на базе теплового насоса должны хорошо соответствовать друг другу по мощности, температуре и остальным параметрам. Неправильный выбор геотермального контура для отбора тепловой энергии грунта может привести к отключению или выходу из строя теплового насоса [2]. При этом обустройство геотермальных скважин является одной из наиболее затратных составляющих теплоснабжения на базе тепловых насосов. Увеличение глубины или количества скважин приводит к экономической нецелесообразности данного вида теплоснабжения. Поэтому корректная оценка требуемой глубины и количества скважин является важной задачей.
В данной работе предложена методика определения требуемой длины вертикального геотермального контура, которая учитывает среднюю годовую тепловую нагрузку на тепловой насос и геотермальный контур, среднемесячную нагрузку и пиковую тепловую нагрузку при расчетных параметрах (например, в наиболее холодную пятидневку с обеспеченностью 0,92).
Теоретические положения
Линейная плотность теплового потока от грунта к геотермальной скважине может быть определена по формуле [3]:
![]() (1)
(1)
![]() (2)
(2)
где t – время, Tg – температура грунта вдали от геотермальных скважин может быть принята плюс 8 оС, Tb – температура поверхности обсадной трубы геотермальной скважины, Rq(t) – термическое сопротивление теплопередаче от грунта к геотермальной скважине, λg – теплопроводность грунта, ag – температуропроводность грунта, H – глубина скважин, rb – наружный диаметр скважины.
Функция g(t) является безразмерным термическим сопротивлением поля геотермальных скважин и называется g-функцией [3]. При расчете g-функции геометрические параметры нормируются на глубину скважин H, а временные параметры на характерное время ts = H2/(9ag).
На рисунке 1 приведены зависимости g-функции от времени для одной геотермальной скважины и квадратного поля геотермальных скважин с размерами 2х2, 4х4, 8х8 скважин. Глубина скважин 40 м, наружный диаметр обсадной трубы скважин 150 мм, температуропроводность грунта ag = 10−6 м2/с, расстояние между скважинами по обеим координатам 7,5 м.
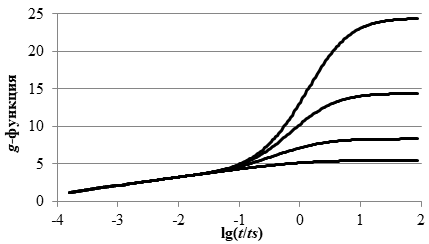
Рис. 1 – Безразмерное термическое сопротивление (g-функция) одиночной геотермальной скважины (нижняя кривая) и поля геотермальных скважин (снизу вверх) 2х2, 4х4, 8х8 скважин
На рисунке 1 видно, что термическое сопротивление скважин увеличивается со временем, при этом можно выделить три характерных временных диапазона.
В диапазоне от нуля до момента времени ts/10 (ближняя асимптотика) термическое сопротивление скважин не зависит от геометрии поля скважин, то есть отдельные скважины не влияют друг на друга. Данный период крайне важен для анализа, поскольку при указанных параметрах характерное время ts составляет 5,5 лет. Соответственно ближняя асимптотика занимает временной диапазон до 0,55 года, что приблизительно равно отопительному периоду для климатических условий большей части России.
Во втором временном диапазоне от ts/10 до 10ts (переходный период от 0,55 до 55 лет) происходит основное увеличение термического сопротивления поля геотермальных скважин. Например, для поля размером 8х8 скважин безразмерное термическое сопротивление после первого отопительного сезона составит приблизительно 4,8, а после второго отопительного сезона уже 7,8. То есть термическое сопротивление увеличится, а теплоотдача от скважин уменьшится в 1,6 раза.
В третьем временном диапазоне (дальняя асимптотика, более 10ts или более 55 лет) термическое сопротивление практически не изменяется и для поля размером 8х8 скважин равняется 25, что в 5 раз больше термического сопротивления после первого отопительного периода.
Учитывая вышесказанное, расчет длины геотермальных скважин должен учитывать среднегодовое потребление тепловой энергии, среднемесячное потребление тепловой энергии в месяц наибольшего потребления и максимальное теплопотребление при расчетных параметрах. В данной работе предложено следующее выражение:
![]() (3)
(3)
где Qy - среднегодовая мощность скважины; Qm - среднемесячная мощность скважины в месяц наибольшего теплопотребления; Qh - мощность скважины при пиковом расчетном теплопотреблении; Ry - термическое сопротивление поля скважин для среднегодового потребления; Rm - термическое сопротивление поля скважин для среднемесячного потребления; Rh - термическое сопротивление поля скважин для расчетного периода; Rb - термическое сопротивление, учитывающее внутреннюю конфигурацию скважины; Tгр - температура грунта вдали от скважинного поля; Tcin - минимально допустимая температура антифриза внутри скважины по условиям безаварийной работы теплового насоса.
Очевидно, что для среднемесячного теплопотребления и пикового теплопотребления термическое сопротивление должно приниматься за месяц эксплуатации и за расчетный период (например, пятидневку). При этом термическое сопротивление будет находиться в области ближней асимптотики, для которой существует инженерная формула [3]. Например, для пятидневки и месячного периода значения g-функции равны gh = 1,242, gm = 3,426.
Для определения Rb можно использовать следующую формулу [6], [7], [8]
где λгр - теплопроводность грунта; λp - теплопроводность материала труб с антифризом, Вт/(моС); db - диаметр скважины; dpн - наружный диаметр труб с антифризом; dpв - внутренний диаметр труб с антифризом; s - расстояние между центрами U-образной трубы с антифризом, м.
Термическое сопротивление грунта для среднегодового потребления тепловой энергии можно принимать для дальней асимптотики (см. рисунок 1), так как многие производители гарантируют безаварийную эксплуатацию тепловых насосов в течение длительного периода (от 20 до 50 лет), а срок эксплуатации геотермальных скважин часто принимают еще больше (от 60 до 80 лет).
Пример расчета
В качестве примера был выполнен подбор теплового насоса и расчет поля геотермальных скважин для одноэтажного жилого дома площадью 105 м2, расположенного в пригороде г. Хабаровска. Расчетные условия приняты для г. Хабаровска: температура воздуха наиболее холодной пятидневки с обеспеченностью 0,92 минус 29оС; продолжительность отопительного периода 204 суток; средняя температура отопительного периода минус 9,5оС. Воздухообмен принимался равным однократному воздухообмену в жилых комнатах и составил приблизительно 205 м3/ч. Для горячего водоснабжения (ГВС) принимался электрический бойлер с электронагревателем мощностью 2 кВт. При расчете среднемесячного потребления энергии на горячее водоснабжение общий расход воды принимался равным 20 м3/мес на четверых проживающих. Нагрев горячей воды осуществляется в баке-накопителе до температуры внутреннего контура теплового насоса, затем в электрическом бойлере до температуры 65оС. Расчетная тепловая нагрузка на систему отопления с учетом рекуперации теплоты удаляемого вентиляционного воздуха составила 6,39 кВт. Среднемесячная тепловая нагрузка на тепловой насос для горячего водоснабжения составила 0,47 кВт.
Таким образом, пиковое теплопотребление для наиболее холодной пятидневки с обеспеченностью 0,92 составляет 6860 Вт. Для наиболее холодного месяца средняя нагрузка на систему отопления и ГВС составит 4915 Вт. Среднегодовая нагрузка на систему отопления и ГВС с учетом теплопоступлений составляет 2570 Вт.
По результатам расчета тепловых потерь жилого дома были подобраны электрические парокомпрессионные геотермальные тепловые насосы DanHeat D&S-9 (HC) или аналог SPRSUN CGD-9 (HC). Оба тепловых насоса представляют собой моноблочные конструкции и имеют сходные характеристики: номинальную мощность нагрева 9,9 кВт; охлаждения 8,4 кВт; потребляемую электрическую мощность в режиме нагрева 1,92 кВт, в режиме охлаждения 1,7 кВт; температурный диапазон наружного контура (температура антифриза, поступающего в теплообменный аппарат) от минус 3 оС до плюс 30 оС; максимальная температура нагрева плюс 60оС. На сайте производителя приведены все характеристики, необходимые для расчета, проектирования и моделирования работы тепловых насосов в указанных диапазонах температур.
Как было указано, среднегодовая нагрузка на систему отопления и ГВС с учетом теплопоступлений составляет 2570 Вт. При расчетном коэффициенте преобразования тепловой энергии равном 4,2 среднегодовая мощность, потребляемая из скважин, составит 2570 × (4,2 - 1) / 4,2 = 1960 Вт. Среднегодовая нагрузка на систему кондиционирования (при тепловом насосе отопление / охлаждение и установленных фанкойлах) составит 345 Вт, поэтому при расчетном коэффициенте охлаждения 4,0 получим среднегодовую мощность, возвращаемую в скважину, равной 345 × (4,0 + 1) / 4,0 = 430 Вт. Таким образом, в среднем за год из скважин будет потребляться мощность 1530 Вт.
Аналогичным образом можно получить, что для наиболее холодного месяца среднемесячная тепловая мощность, потребляемая из скважины, составит 3740 Вт. Пиковая тепловая мощность, потребляемая из скважины, составит 5220 Вт.
При приведенных параметрах и теплопроводности грунта 1,7 Вт/(моС) требуемая длина скважины согласно формуле составит
Из расчета видно, что для обеспечения работы теплового насоса необходимо восемь скважин по 40 м каждая. При этом в условиях климата г. Хабаровска треть скважин необходимы для обеспечения работы теплового насоса в течение длительного периода, треть скважин необходимы для обеспечения работы насоса в наиболее холодный месяц и треть скважин необходимы для обеспечения пиковых нагрузок в течение наиболее холодной пятидневки.
Отметим, что часто для расчета требуемой длины геотермальной скважины используется упрощенная методика, основанная на величине удельного теплосъема 50 Вт/м [1], [2]. Согласно данной методике, требуемая длина скважины для теплового насоса DanHeat D&S-9 (HC) составит (9900 – 1900) / 50 = 160 м, то есть в 2 раза меньше.
Нами было выполнено моделирование температуры для поля из четырех геотермальных скважин прямоугольной формы 2 х 2 и для поля из восьми геотермальных скважин 2 х 4. Глубина каждой скважины составляла 40 м в обоих случаях. Суммарная длина скважин в первом случае составила 160 м, во втором – 320 м.
Моделирование проведено для тридцатилетнего периода с усреднением всех параметров по месяцам. Начальным месяцем моделирования был октябрь 2009 года. Среднемесячные параметры наружного воздуха для первых 10 лет принимались фактическими для г. Хабаровска (с 2009 по 2019 год), для следующих 20 лет среднемесячными по СП «Строительная климатология». Результаты моделирования приведены на рисунках 2 и 3.
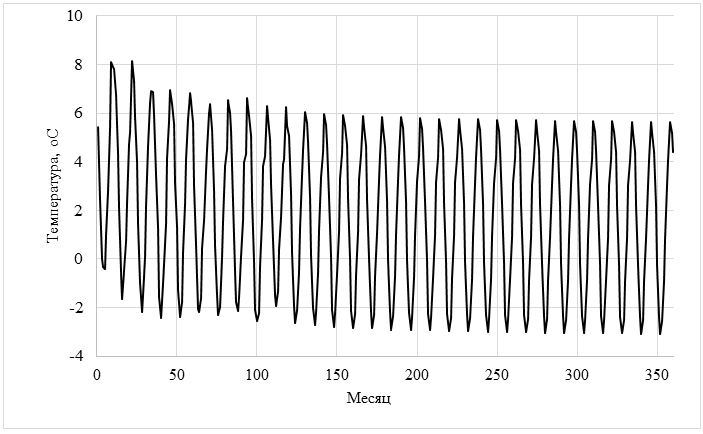
Рис. 2 - Температура скважин в зависимости от месяца эксплуатации для поля скважин 2 х 2. Скважины имеют длину 40 м каждая
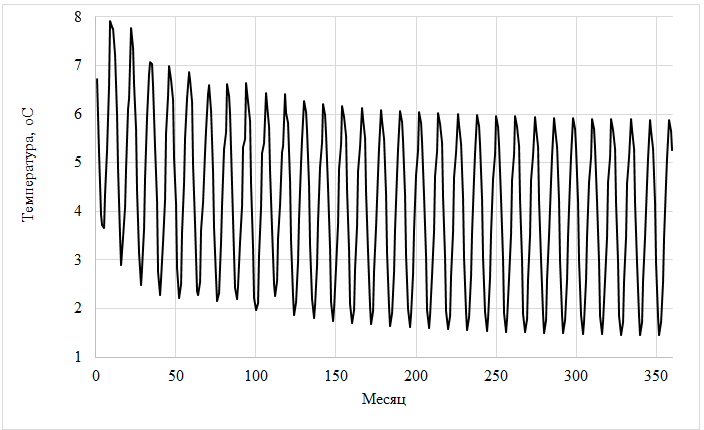
Рис. 3 - Температура скважин в зависимости от месяца эксплуатации для поля скважин 2 х 4. Скважины имеют длину 40 м каждая
На рисунке 2 видно, что при суммарной длине скважин 160 м температура антифриза в первый же отопительный сезон опускается ниже 0 оС. Как было указано выше, минимальная температура скважины составляет минус 3 оС. Поэтому при пиковом потреблении тепловой энергии в наиболее холодный период января аварийное отключение теплового насоса может произойти уже в первый отопительный сезон. Что и случилось с несколькими геотермальными насосами, установленными в пригороде г. Хабаровска в 2016 – 2018 годах.
При суммарной длине скважин 320 м сохраняется запас по температуре скважин 4,5 оС, который обеспечит бесперебойную работу теплового насоса в течение многолетнего периода эксплуатации.
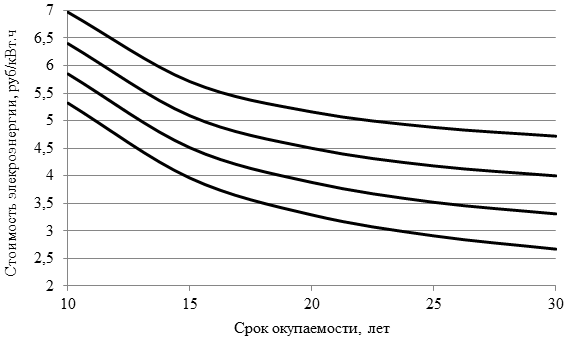
На рисунке 4 приведены дисконтированные сроки окупаемости теплового насоса в зависимости от стоимости электрической энергии для норм дисконта от 5% (безрисковая составляющая нормы дисконта) до 11% (безрисковая и инфляционная составляющие нормы дисконта). Сравнение было проведено для отопления рассмотренного выше жилого дома с помощью теплового насоса DanHeat D&S-9 (HC) и электрического котла ZOTA-9 «Lux».
Рис. 4 - Требуемая стоимость электрической энергии в зависимости от срока окупаемости для норм дисконта 5% (нижняя кривая), 7%, 9% и 11% (верхняя кривая)
Из графиков, приведенных на рисунке 4, видно, что срок окупаемости геотермальных тепловых насосов при благоприятном инвестиционном климате (норме дисконта 5%) и текущей стоимости электрической энергии составляет не менее 15 лет.
Срок окупаемости тепловых насосов можно существенно уменьшить, если проводить мероприятия по восстановлению теплоты грунта в летний период. В этом случае в формуле (5) первое слагаемое будет равно нулю, и требуемая суммарная длина скважин уменьшится на 111,7 м и составит около 210 м. Это приведет к уменьшению первоначальных инвестиций в устройство геотермального теплового насоса на 200 тысяч рублей.
Использование мероприятий по восстановлению теплоты грунта в летний период является на данный момент актуальным направлением исследований [9], [10]. После отопительного периода грунт имеет температуру около 0 °С. Поэтому для восстановления теплоты грунта в летний период могут быть использованы вакуумные солнечные коллекторы, плоские солнечные коллекторы, открытые солнечные коллекторы [10], воздушные отопительные агрегаты типа Volcano, установленные снаружи здания, и другие. На первый взгляд открытые солнечные коллекторы и воздушные отопительные агрегаты кажутся наиболее перспективными, так как имеют невысокую стоимость и могут работать круглосуточно, нагревая грунт за счет температуры наружного воздуха даже в ночные часы. Однако, анализ совместной работы геотермальных тепловых насосов и устройств, восстанавливающих теплоту грунта в летний период, требует проведения дополнительных исследований.
Заключение
В данной работе предложена методика определения требуемой длины геотермальных скважин для тепловых насосов типа «грунт» − «вода» на основе трех составляющих: среднегодового потребления тепловой мощности, среднемесячного потребления тепловой мощности в наиболее холодный месяц и пикового потребления тепловой мощности в расчетный период (например, наиболее холодную пятидневку с обеспеченностью 0,92). К достоинствам предложенной методики можно отнести следующее. Во-первых, методика позволяет провести анализ составляющих требуемой длины. Например, данная методика позволяет оценить: насколько уменьшится требуемая длина скважин при использовании резервного источника тепловой энергии в пиковом режиме потребления; насколько уменьшится требуемая длина скважин при восстановлении теплоты грунта в летний период. Во-вторых, для расчета требуемой длины скважин используются достаточно простые инженерные формулы, не требующие годового моделирования работы скважин и теплового насоса. Исключение составляет только расчет термического сопротивления грунта для периода 10 и более лет, который может быть проведен с использованием библиотеки для языка программирования Python [4].
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Крылов Э. Г. Комбинированная система отоплении здания в сельской местности с применением тепловых насосов / Э. Г. Крылов, З. С. Саидова // Международный научно-исследовательский журнал. – 2015. − № 3 (34), часть 1. – С. 78 – 80.
- Москаленко И.В. Тепловые насосы. Практический опыт внедрения и проблемы рынка / И.В. Москаленко // Сантехника, отопление, кондиционирование. – 2018. − № 3. – С. 54-67.
- Eskilson P. Thermal analysis of heat extraction boreholes / P. Eskilson. – Sweden: University of Lund, Department of Mathematical Physics, 1987. – 222 p.
- Cimmino M. pygfunction: an open-source toolbox for the evaluation of thermal response factors for geothermal borehole fields / M. Cimmino // The Canadian Chapter of the International Building Performance Simulation Association : Proceedings of eSim 2018, the 10th conference of IBPSA, Canada, May 9-10, 2018. – Canada, Montreal. – P. 492-501.
- Cimmino, M. Fast calculation of the g-functions of geothermal borehole fields using similarities in the evaluation of the finite line source solution / M. Cimmino // Journal of Building Performance Simulation. – 2018. − 11(6). − P. 655-668.
- Xuedan Zhang Comparison of Four Methods for Borehole Heat Exchanger Sizing Subject to Thermal Response Test Parameter Estimation / Xuedan Zhang, Tiantian Zhang, Bingxi Li, Yiqiang Jiang // Energies. – 2019. − № 12, 4067.
- Rolando, D. A Web Application for Geothermal Borefield Design / D. Rolando, J. Acuna, M. Fossa // Proceedings World Geothemal Congress, Australia, Melbourne, 19-25 April, 2015. – P. 1-10. [Electronic resource] – URL: https://www.kth.se/polopoly_fs/1.571174.1550157681!/rolando%20et%20%20al%20web%20application.pdf (accessed 01.10.2020).
- Claesson, J. An analytical method to calculate borehole fluid temperatures for time-scales from minutes to decades / J. Claesson, S. Javed // ASHRAE Transactions. – 2011. − vol. 117(2), P. 279-288.
- Lei Xia Performance Simulation of a Ground Source Heat Pump System Integrated with Solar Photovoltaic Thermal Collectors for Residential Applications / Lei Xia, Zhenjun Ma, G. Kokogiannakis // Building Simulation 2017 : Proceedings of the 15th IBPSA Conference San Francisco, CA, USA, Aug. 7-9, 2017. – USA, 2017. – P. 839-847.
- Bertram E. Heat Pump Systems with Vertical Ground Heat Exchanger and Uncovered Solar Thermal Collectors / E. Bertram. – Umschlag: MV-Verlag, 2015. – 258 p.
Список литературы на английском языке/ References in English
- Krylov Je. G. Kombinirovannaja sistema otoplenii zdanija v sel'skoj mestnosti s primeneniem teplovyh nasosov [The combined heating system of building in countryside with heating pumps] / Je. G. Krylov, Z. S. Saidova // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Research Journal]. – 2015. − № 3 (34), part 1. – P. 78 – 80. [in Russian]
- Moskalenko I.V. Teplovye nasosy. Prakticheskij opyt vnedrenija i problemy rynka [Heating pumps. Practical experience of application and market problems] / I.V. Moskalenko // Santehnika, otoplenie, kondicionirovanie [Sanitary engineering, heating, air conditioning]. – 2018. − № 3. – P. 54-67. [in Russian]
- Eskilson P. Thermal analysis of heat extraction boreholes / P. Eskilson. – Sweden: University of Lund, Department of Mathematical Physics, 1987. – 222 p.
- Cimmino M. pygfunction: an open-source toolbox for the evaluation of thermal response factors for geothermal borehole fields / M. Cimmino // The Canadian Chapter of the International Building Performance Simulation Association : Proceedings of eSim 2018, the 10th conference of IBPSA, Canada, May 9-10, 2018. – Canada, Montreal. – P. 492-501.
- Cimmino, M. Fast calculation of the g-functions of geothermal borehole fields using similarities in the evaluation of the finite line source solution / M. Cimmino // Journal of Building Performance Simulation. – 2018. − 11(6). − P. 655-668.
- Xuedan Zhang Comparison of Four Methods for Borehole Heat Exchanger Sizing Subject to Thermal Response Test Parameter Estimation / Xuedan Zhang, Tiantian Zhang, Bingxi Li, Yiqiang Jiang // Energies. – 2019. − № 12, 4067.
- Rolando, D. A Web Application for Geothermal Borefield Design / D. Rolando, J. Acuna, M. Fossa // Proceedings World Geothemal Congress, Australia, Melbourne, 19-25 April, 2015. – P. 1-10. [Electronic resource] – URL: https://www.kth.se/polopoly_fs/1.571174.1550157681!/rolando%20et%20%20al%20web%20application.pdf (accessed 01.10.2020).
- Claesson, J. An analytical method to calculate borehole fluid temperatures for time-scales from minutes to decades / J. Claesson, S. Javed // ASHRAE Transactions. – 2011. − vol. 117(2), P. 279-288.
- Lei Xia Performance Simulation of a Ground Source Heat Pump System Integrated with Solar Photovoltaic Thermal Collectors for Residential Applications / Lei Xia, Zhenjun Ma, G. Kokogiannakis // Building Simulation 2017 : Proceedings of the 15th IBPSA Conference San Francisco, CA, USA, Aug. 7-9, 2017. – USA, 2017. – P. 839-847.
- Bertram E. Heat Pump Systems with Vertical Ground Heat Exchanger and Uncovered Solar Thermal Collectors / E. Bertram. – Umschlag: MV-Verlag, 2015. – 258 p.