СВОЙСТВО ХОРОШЕГО ОТОБРАЖЕНИЯ
Научная статья
Терновых И.И.
Воронежский государственный университет, Воронеж, Россия
Аннотация
В данной статье рассматривается устойчивость нечеткой дискретной системы, проводится анализ устойчивости в зависимости от вида матрицы отношений, выводится устойчивость на основе свойства хорошего отображения.
Ключевые слова: свойство хорошего отображения, устойчивость решения нечеткой дискретной системы, функция принадлежности
Мы рассматривали нечеткую дискретную систему с матрицей отношений , полученную последовательностью импликаций длинной равной 1. Рассмотрим теперь длину
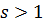
. Пусть
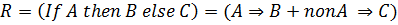
. Представим элементы матрицы R следующим образом:
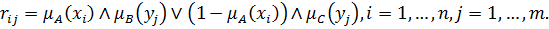
Если мы выберем в качестве компонентов матрицы отношений произвольные нечеткие множества A, B, C , тогда мы не всегда получим следующие равенства
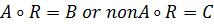
.
Рассмотрим следующий пример:
Пример 3.
Пусть
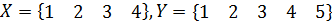
,
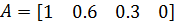
,

,
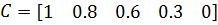
,
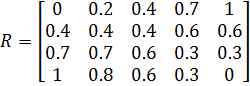
.
Получим
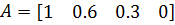
, но
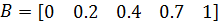
.
Тогда
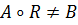
. Тоже самое получим для

.
Определение 2. Пусть дана матрица
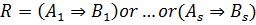
. Тогда скажем, что матрица R обладает свойством хорошего отображения, если и только если для каждого
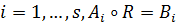
.
Свойство хорошего отображения матрицы R зависит от выбора нечетких множеств A
i, B
i. Рассмотрим теперь свойства нечетких множеств A
i, B
i для определения наличия или отсутствия свойства хорошего отображения.
Утверждение 1. Пусть дана матрица нечеткого отношения
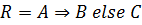
. Тогда
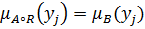
при условии, что
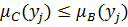
и
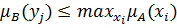
.
Доказательство.
Очевидно, что
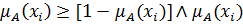
. Объединяя это с предположением
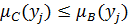
, получим следующее:
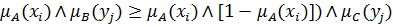 .
.
Отметим, что
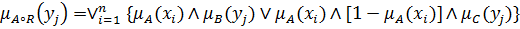
,
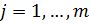
.
Принимая во внимание предыдущее неравенство, получим
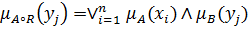
, но это значит, что
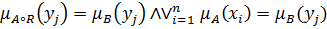
. Видно, что это равенство является последним предположением утверждения 1:
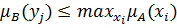
. В примере 3
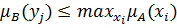
верно для любого y, и выполнено следующее:
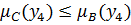
,
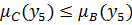
. В соответствии с утверждением 1 мы видим на рисунке (), что
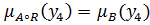
и
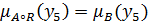
. Стоит отметить также, что
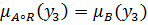
, но
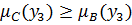
. Это обозначает, что обратная импликация в утверждении 1 не выполнена.
Утверждение 1 можно симметрично формулировать для случая с нечеткими множествами вида:
non A, C.
Утверждение 2.



Список литературы / References
- Glas M. Theory of fuzzy systems.//Fuzzy sets and systems. – 1983. – 10. – P. 65-77
- Е.В. Ивохин, С.О.Волчков. Исследование динамики нечетких дискретных систем //System research & Information Technologies. – 2005. – 4. – P. 94 – 105
- Леденева Т.М. Обработка нечеткой информации. – Воронеж.:ВГУ, 2006. – 233 с.
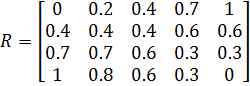 .
Получим
.
Получим
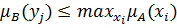 . В примере 3
. В примере 3 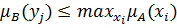 верно для любого y, и выполнено следующее:
верно для любого y, и выполнено следующее: 


