РОЛЬ АТМОСФЕРНОЙ ТУРБУЛЕНТНОСТИ В ГЕНЕРАЦИИ ЗАВИХРЕННОСТИ ТАЙФУНОВ И ТОРНАДО
Маслов С.А.1, Смирнов В.А.2, Харчевский А.А.3
1ORCID: 0000-0001-8440-2821, младший научный сотрудник,
Объединенный институт высоких температур РАН, г. Москва;
2ORCID: 0000-0002-3853-3369, аспирант,
3ORCID: 0000-0002-4404-4203, аспирант,
Московский технологический университет (МИРЭА), г. Москва
Исследование проводилось при финансовой поддержке РФФИ (проект № 16-31-00456 мол_а)
РОЛЬ АТМОСФЕРНОЙ ТУРБУЛЕНТНОСТИ В ГЕНЕРАЦИИ ЗАВИХРЕННОСТИ ТАЙФУНОВ И ТОРНАДО
Аннотация
На основе двумасштабной гидродинамической модели, учитывающей влияние турбулентных пульсаций на средний поток, построен механизм генерации завихренности тайфунов и торнадо за счет атмосферной турбулентности. Проведен вейвлет-анализ флуктуаций давления в реальных атмосферных вихрях – торнадо и ураганах Айрин и Андреа. Найдены характерные частоты флуктуаций атмосферного давления, а также получены оценки влияния турбулентных пульсаций на усиление завихренности в тайфунах и торнадо. Вклад турбулентного механизма может быть сравним с влиянием растяжения вихревых линий.
Ключевые слова: вейвлет-анализ, турбулентность, тайфун, торнадо.
Maslov S.A.1, Smirnov V.A.2, Kharchevsky A.A.3
1ORCID: 0000-0001-8440-2821, Junior researcher,
Joint Institute for High Temperatures (JIHT), RAS, Moscow
2ORCID: 0000-0002-3853-3369, Postgraduate student,
3ORCID: 0000-0002-4404-4203, Postgraduate student,
2,3Moscow Technological University (MIREA), Moscow
This study was supported by the Russian Foundation for Basic Research (Project No. 16-31-00456 Mol_a)
ROLE OF AIR TURBULENCE IN GENERATION OF VORTICITY OF TYPHOONS AND TORNADO
Abstract
Based on a two-scale hydrodynamic model considering the influence of turbulent pulsations on the average flow, a mechanism is developed for generating vorticity of typhoons and tornadoes due to atmospheric turbulence. A wavelet-analysis of pressure fluctuations in real atmospheric vortexes, tornadoes and hurricanes, Irene and Andrea is conducted in the paper. The characteristic frequencies of atmospheric pressure fluctuations are found, also the estimates of the influence of turbulent pulsations on the enhancement of vorticity in typhoons and tornadoes are obtained. The contribution of the turbulent mechanism can be compared with the effect of the stretching of the vortex lines.
Keywords: wavelet-analysis, turbulence, typhoon, tornado.
Торнадо (смерч) и тайфун (тропический ураган) – наиболее интенсивные атмосферные вихри. Радиус тайфуна составляет 500 – 1000 км, максимальная азимутальная скорость – до 90 м/с. Скорость вращения торнадо, несмотря на меньшие, чем у тайфуна, поперечные размеры (10 – 1500 м), может превышать 150 м/с [1, С. 186]. Вследствие больших скоростей потока в атмосферных вихрях имеют место сильные перепады атмосферного давления: в ядре тайфуна и торнадо давление иногда на 15 – 20% ниже, чем на периферии.
Большие градиенты скорости и давления в атмосферных вихрях обусловливают трудности их численного моделирования. Кроме того, на генерацию завихренности оказывают влияние различные факторы – как термогидродинамические [2, С. 125], [3, C. 466], так и электромагнитные [4, C. 34], [5, C. 56]. В атмосферных вихрях также имеет место интенсивная турбулентность потока. Для оценки частоты турбулентных пульсаций давления и скорости необходимо проводить натурные наблюдения и применять методы обработки экспериментальных данных – Фурье- или вейвлет-анализ [6, C. 33]. Первая методика, основанная на использовании преобразования Фурье, отражает частотные закономерности процессов, а вейвлет-анализ позволяет выявить как частотные, так и пространственно-временные закономерности, поэтому больше подходит для исследования нестационарных процессов таких, как интенсивные атмосферные вихри.
В настоящей статье предлагается турбулентный механизм генерации завихренности в тайфунах и торнадо. Оценки, полученные с помощью вейвлет-анализа данных натурных наблюдений, показывают, что турбулентные пульсации давления и скорости могут оказывать существенное влияние на интенсификацию завихренности.
Рассмотрим турбулентное движение воздуха в интенсивных атмосферных вихрях. Среду полагаем несжимаемой, так как характерная скорость потока в тайфунах и торнадо обычно меньше скорости звука. Следуя [7, C. 191], будем описывать турбулентное движение несжимаемой среды системой уравнений неразрывности и Навье – Стокса:
![]() (1)
(1)
![]()
Здесь ![]() – турбулентные пульсации скорости и давления, для которых справедливо
– турбулентные пульсации скорости и давления, для которых справедливо
![]() (2)
(2)
а треугольные скобки ![]() в формулах (1) – (2) обозначают операцию осреднения, которую для произвольной физической характеристики f в момент времени t0 определим как
в формулах (1) – (2) обозначают операцию осреднения, которую для произвольной физической характеристики f в момент времени t0 определим как
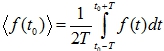 (3)
(3)
где T – промежуток времени, малый по сравнению со временем жизни атмосферного вихря (тайфуна или торнадо) и большой в сравнении с периодом турбулентных пульсаций. Предполагается, что характерный размер пульсаций ![]() существенно меньше пространственного масштаба R среднего потока.
существенно меньше пространственного масштаба R среднего потока.
Из уравнения Навье – Стокса путем взятия ротора от обеих частей второго уравнения (1) получаем уравнение завихренности [8, C. 41]:
![]() (4)
(4)
где ![]() – завихренность потока, для которой также справедливо разложение на среднюю
– завихренность потока, для которой также справедливо разложение на среднюю ![]() и пульсационную
и пульсационную ![]() составляющие:
составляющие:
![]()
Поставляя последнее разложение в уравнение (4) и применяя операцию осреднения, определяемую формулой (3), получаем выражение для средней завихренности:
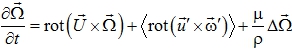 (5)
(5)
где первый член правой части отражает влияние растяжения вихревых линий, второй – воздействие атмосферной турбулентности. Для оценки вклада турбулентных пульсаций оценим отношение величин первых двух слагаемых правой части (5):
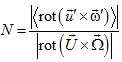 (6)
(6)
Обозначим характерные скорость и завихренность среднего потока как U, Ω, пульсации величин – соответственно ![]() . Числитель и знаменатель (6) имеют порядки
. Числитель и знаменатель (6) имеют порядки ![]() и UΩ/R соответственно,
и UΩ/R соответственно, ![]() . Кроме того, характерную пульсационную завихренность можно оценить как
. Кроме того, характерную пульсационную завихренность можно оценить как ![]() , где частота флуктуаций
, где частота флуктуаций![]() находится посредством вейвлет-анализа данных натурных наблюдений. Из (5) – (6) следует, что относительный вклад турбулентности в генерацию завихренности тайфунов и торнадо приближенно определяется величиной
находится посредством вейвлет-анализа данных натурных наблюдений. Из (5) – (6) следует, что относительный вклад турбулентности в генерацию завихренности тайфунов и торнадо приближенно определяется величиной
![]() (7)
(7)
Для оценки частоты пульсаций проведено сравнение частотно-временной эволюции атмосферного давления на земной поверхности в следующих типичных случаях атмосферных вихрей: торнадо [9] (Пратт, Канзас, США, 07.05.2002), тайфунов Айрин [10] (15 – 29.08.2011, США) и Андреа [11] (06.2013, США). Давление вблизи торнадо измерялось с использованием закрепленного на земной поверхности зонда HITPR [9], оцифровка экспериментальных данных в области прохождения торнадо производилась с частотой 10 Гц. Измерение давления в ураганах проводилось в штате Северная Каролина (США) 26 – 28.08.2011 с применением наземных экспериментальных установок NOAA [10], [11]. Обработка экспериментальных данных проводилась на языке MATLAB с использованием вейвлета Хаара, успешность применения которого для плазменных и атмосферных процессов отмечалась в [12].
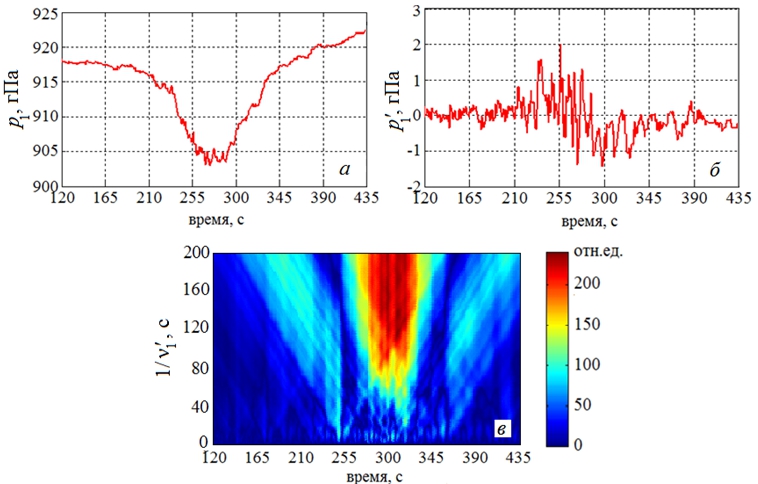
На рис. 1 – 2 приведены результаты измерения атмосферного давления и вейвлет-анализа его флуктуаций для торнадо и тайфунов. Вейвлет-анализ показывает сильный рост флуктуаций давления в периоды его существенного отклонения от нормального (т.е. вблизи ядра торнадо или глаза тайфуна): на 210 – 345 секундах с момента начала эксперимента в торнадо (рис. 1а), в районе 08:00 – 16:00 27.08.2011 г. (по местному времени) в тайфуне Айрин и в 10:00 – 20:00 06.06.2013 г. в урагане Андреа. Абсолютное изменение давления в атмосферных вихрях составляло 15 – 50 гПа (рис. 1 – 2). Характерная частота колебаний давления, а следовательно, и турбулентных пульсаций завихренности, для торнадо в Канзасе имела порядок ![]() (рис. 1в), максимальная азимутальная скорость потока U1=31 м/с, давление резко изменялось в интервале времени 210 – 345 с [9]. В дальнейшем индекс «1» будем использовать для обозначения характеристик торнадо, индексы «2» и «3» - для тайфунов Айрин и Андреа. Если считать, что скорость поступательного перемещения воронки около 10 м/с, то радиус торнадо имеет порядок 500 м. Радиус ядра полагаем равным R1=250 м. Из соотношения (7) получаем, что для торнадо в Канзасе N1 ~ 0,25.
(рис. 1в), максимальная азимутальная скорость потока U1=31 м/с, давление резко изменялось в интервале времени 210 – 345 с [9]. В дальнейшем индекс «1» будем использовать для обозначения характеристик торнадо, индексы «2» и «3» - для тайфунов Айрин и Андреа. Если считать, что скорость поступательного перемещения воронки около 10 м/с, то радиус торнадо имеет порядок 500 м. Радиус ядра полагаем равным R1=250 м. Из соотношения (7) получаем, что для торнадо в Канзасе N1 ~ 0,25.
Рис. 1 – Эволюция давления в торнадо (Пратт, Канзас, 7.05.2002) (а), флуктуации атмосферного давления (б), вейвлет-спектр флуктуаций давления (в)
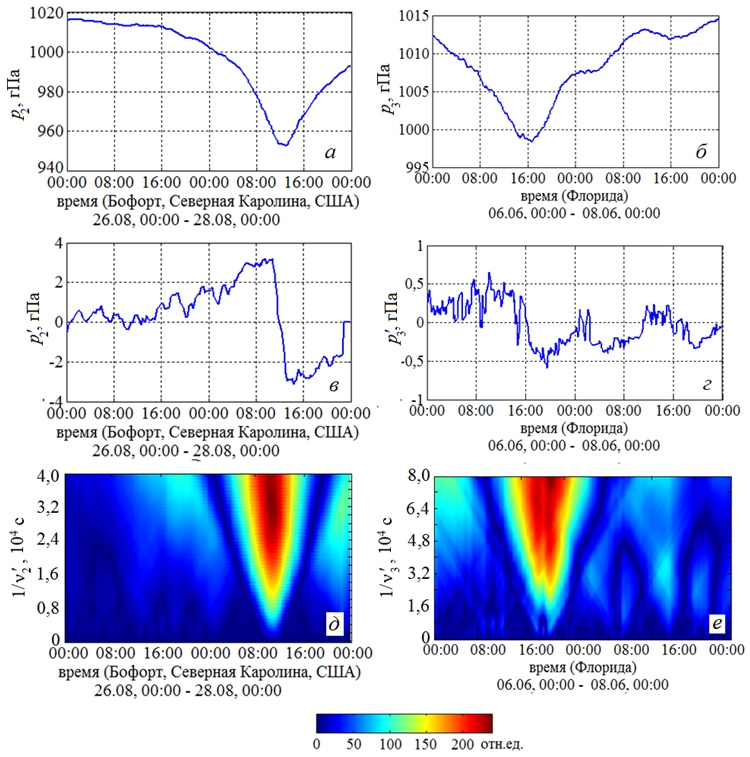
Влияние турбулентности на генерацию завихренности в тайфунах также оцениваем по формуле (7). Характерные частоты турбулентных пульсаций составляют![]() ,
, ![]() (рис. 2 д,е). Размер урагана обычно имеет порядок 500 – 1000 км, радиус глаза считаем равным R2=R3~ 100 км. Максимальные азимутальные скорости в тайфунах равнялись U2=54 м/с [10], U3=35 м/с [11]. Формула (7) дает следующие оценки относительного влияния турбулентности: N2~0,34, N3~0,13. Следовательно, вклад турбулентности в интенсификацию завихренности потока может быть сравним с влиянием растяжения вихревых линий.
(рис. 2 д,е). Размер урагана обычно имеет порядок 500 – 1000 км, радиус глаза считаем равным R2=R3~ 100 км. Максимальные азимутальные скорости в тайфунах равнялись U2=54 м/с [10], U3=35 м/с [11]. Формула (7) дает следующие оценки относительного влияния турбулентности: N2~0,34, N3~0,13. Следовательно, вклад турбулентности в интенсификацию завихренности потока может быть сравним с влиянием растяжения вихревых линий.
Рис. 2 – Изменение давления в тайфунах Айрин (а) и Андреа (б), флуктуации давления в тайфунах (в, г), вейвлет-спектры флуктуаций давления в ураганах Айрин (д) и Андреа (е)
На основе гидродинамических уравнений исследован механизм генерации завихренности тайфунов и торнадо за счет атмосферной турбулентности. С помощью вейвлет-анализа натурных данных определена характерная частота турбулентных пульсаций. Получено, что в исследованных вихрях вклад турбулентности в завихренность среднего потока составляет до 35% от влияния растяжения вихревых линий. Таким образом, показано, что ролью турбулентности в генерации завихренности нельзя пренебрегать в ходе теоретического исследования интенсивных атмосферных вихрей.
Список литературы/References
- Наливкин Д.В. Ураганы, бури и смерчи. Географические особенности и геологическая деятельность / Д.В. Наливкин. – Л.: Наука, 1969. – 487 с.
- Арсеньев С.А. Теория мезомасштабной турбулентности. Вихри атмосферы и океана / С.А. Арсеньев, В.А. Бабкин, А.Ю. Губарь и др.; под общ. ред. Г.С. Голицына. – М. – Ижевск: Институт компьютерных исследований, НИЦ «Регулярная и хаотическая динамика», 2010. – 308 с.
- Курганский М.В. Генерация спиральности во влажной атмосфере / М.В. Курганский // Известия РАН. Серия Физика атмосферы и океана. – 1993. – Т. 29. – № 4. – С. 464 – 469.
- Натяганов В.Л., Маслов С.А. Ломоносов и загадки природного электричества. Часть 4. Электромагнитные механизмы формирования торнадоподобного смерча / В.Л. Натяганов, С.А. Маслов // Вестник Московского университета. Серия 1, Математика. Механика. – 2014. – № 2. – С. 32 – 38.
- Маслов С.А. Электрические механизмы усиления завихренности в воронке торнадо / С.А. Маслов // Вестник Московского университета. Серия 1, Математика. Механика. – 2015. – №6. – С. 54 – 58.
- Добеши И. Десять лекций по вейвлетам / И. Добеши. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2004. – 464 с.
- Маслов А.К., Маслов С.А., Панфилов Д. Влияние мелкомасштабной турбулентности на крупномасштабную завихренность / А.К. Маслов, С.А. Маслов, Д. Панфилов // Современные проблемы прикладной математики, теории управления и математического моделирования: материалы IV Международной научной конференции. – Воронеж: Издательско-полиграфический центр ВГУ, 2011. – С. 190 – 192.
- Алексеенко С.В., Куйбин П.А., Окулов В.Л. Введение в теорию концентрированных вихрей / С.В. Алексеенко, П.А. Куйбин, В.Л. Окулов. – Новосибирск: Институт теплофизики СО РАН, 2003. – 504 с.
- Samaras T.M., Lee J.J. Pressure measurements within a large tornado [Electronic resource] / T.M. Samaras, J.J. Lee. – URL: https://ams.confex.com/ams/pdfpapers/74267.pdf (accessed: 24.11.2017).
- Hurricane Irene August 26 – 27, 2011. [Electronic resource]. – URL: http://www.weather.gov/mhx/Aug272011EventReview (accessed: 24.11.2017).
- Tropical Storm Andrea Event Summary. [Electronic resource]. – URL: http://www.weather.gov/tae/event-201306_andrea (accessed: 24.11.2017).
- Maslov S.A. Wavelet analysis of the parameters of edge plasma fluctuations in the L-2M stellarator [Electronic resource]/ S.A. Maslov, D.G. Vasilkov, Yu.V. Kholnov and others// Journal of Physics. Conference Series. – 2016. – V. 666(1). – P. 012009. – URL: http://iopscience.iop.org/article/10.1088/1742-6596/666/1/012009 (accessed: 24.11.2017).
Список литературы на английском языке/References in English
- Nalivkin D.V. Uragany, buri i smerchi. Geograficheskie osobennosti i geologicheskaja dejatel'nost' [Hurricanes, storms and tornadoes. Geographical specialities and geological activity] / D.V. Nalivkin. – L.: Nauka, 1969. – 487 p. [in Russian]
- Arsen'ev S.A. Teorija mezomasshtabnoj turbulentnosti. Vihri atmosfery i okeana [Theory of mesoscale turbulence. Vortices of atmosphere and Ocean] / S.A. Arsen'ev, V.A. Babkin, A.Ju. Gubar' and others; edited by G.S. Golitsyn. M. – Izhevsk: Institut komp'juternyh issledovanij, NIC «Reguljarnaja i haoticheskaja dinamika», 2010. – 308 p. [in Russian]
- Kurganskij M.V. Generacija spiral'nosti vo vlazhnoj atmosfere [Spirality generation in a moist atmosphere] / M.V. Kurganskij // Izvestija RAN. Serija Fizika atmosfery i okeana. [Izvestiya. Atmospheric and Oceanic Physics Series]. – 1993. – V. 29. – N 4. – P. 464 – 469. [in Russian]
- Natjaganov V.L., Maslov S.A. Lomonosov i zagadki prirodnogo jelektrichestva. Chast' 4. Jelektromagnitnye mehanizmy formirovanija tornadopodobnogo smercha [Lomonosov and the enigma of natural electricity. Part 4. Electromagnetic mechanisms of forming a tornado-like whirlwind] / V.L. Natjaganov, S.A. Maslov // Vestnik Moskovskogo universiteta. Serija 1, Matematika. Mehanika [Bulletin of the Moscow University. Series 1. Mathematics. Mechanics]. – 2014. – N 2. – P. 32 – 38. [in Russian]
- Maslov S.A. Jelektricheskie mehanizmy usilenija zavihrennosti v voronke tornado [Electric mechanisms of vorticity amplification in the funnel of a tornado] / S.A. Maslov // // Vestnik Moskovskogo universiteta. Serija 1, Matematika. Mehanika [Bulletin of the Moscow University. Series 1. Mathematics. Mechanics]. – 2015. – N 6. – P. 54 – 58. [in Russian]
- Dobeshi I. Desjat' lekcij po vejvletam [Ten lectures on wavelets] / I. Dobeshi. – Izhevsk: NIC «Reguljarnaja i haoticheskaja dinamika», 2004. – 464 p. [in Russian]
- Maslov A.K., Maslov S.A., Panfilov D. Vlijanie melkomasshtabnoj turbulentnosti na krupnomasshtabnuju zavihrennost' [The influence of small-scale turbulence on large-scale vorticity] / A.K. Maslov, S.A. Maslov, D. Panfilov // Sovremennye problemy prikladnoj matematiki, teorii upravlenija i matematicheskogo modelirovanija: materialy IV Mezhdunarodnoj nauchnoj konferencii. [Modern Problems of Applied Mechanics, Control Theory and Mathematical Modelling: Proceedings of the Fourth International Conference]. – Voronezh: Izdatel'sko-poligraficheskij centr VGU, 2011. – pp. 190 – 192. [in Russian]
- Alekseenko S.V., Kujbin P.A., Okulov V.L. Vvedenie v teoriju koncentrirovannyh vihrej [Introduction to theory of concentrated vortices] / S.V. Alekseenko, P.A. Kujbin, V.L. Okulov. – Novosibirsk: Institut teplofiziki SO RAN, 2003. – 504 p. [in Russian]
- Samaras T.M., Lee J.J. Pressure measurements within a large tornado [Electronic resource] / T.M. Samaras, J.J. Lee. – URL: https://ams.confex.com/ams/pdfpapers/74267.pdf (accessed: 24.11.2017).
- Hurricane Irene August 26 – 27, 2011. [Electronic resource]. – URL: http://www.weather.gov/mhx/Aug272011EventReview (accessed: 24.11.2017).
- Tropical Storm Andrea Event Summary. [Electronic resource]. – URL: http://www.weather.gov/tae/event-201306_andrea (accessed: 24.11.2017).
- Maslov S.A. Wavelet analysis of the parameters of edge plasma fluctuations in the L-2M stellarator [Electronic resource] / S.A. Maslov, D.G. Vasilkov, Yu.V. Kholnov and others// Journal of Physics. Conference Series. – 2016. – V. 666(1). – P. 012009. – URL: http://iopscience.iop.org/article/10.1088/1742-6596/666/1/012009 (accessed: 24.11.2017).