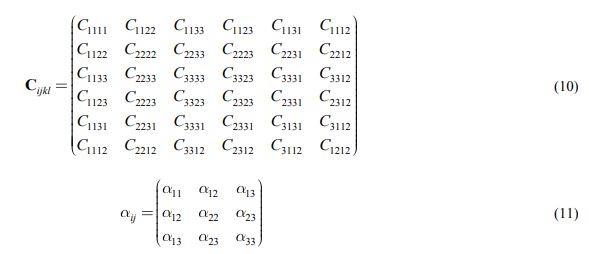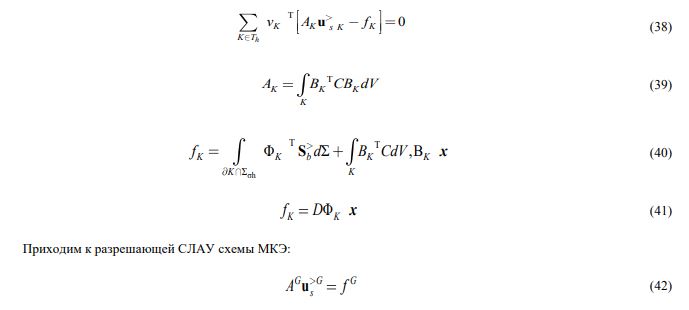РЕШЕНИЕ ЗАДАЧИ ПОЛЗУЧЕСТИ КРИВОЛИНЕЙНО-АНИЗОТРОПНЫХ СРЕД МЕТОДОМ РУНГЕ—КУТТА—ФЕЛЬБЕРГА 5-6 ПОРЯДКА
РЕШЕНИЕ ЗАДАЧИ ПОЛЗУЧЕСТИ КРИВОЛИНЕЙНО-АНИЗОТРОПНЫХ СРЕД МЕТОДОМ РУНГЕ—КУТТА—ФЕЛЬБЕРГА 5-6 ПОРЯДКА
Научная статья
Димитриенко Ю.И.1, Юрин Ю.В.2, Гумиргалиев Т.Р.3, Краснов Г.А.4, *
4 ORCID: 0000-0002-4577-9922;
1, 2, 3, 4 Московский государственный технический университет им. Н.Э. Баумана, Москва, Россия
* Корреспондирующий автор (krasnov14107[at]mail.ru)
АннотацияВ данной работе предложен способ для предварительного анализа на состав и оценку динамики слоев горных пластов глубокого залегания, физических знаний о которых недостаточно или не может быть получено экспериментальным путем без этапа разработки и запуска скважин, рудников и карьеров. Данный способ основан на моделировании напряженно-деформированного состояния горных пород с учетом блочно-криволинейной анизотропии и ползучести. В работе предлагается метод для эффективного численного решения задачи напряженно-деформированного состояния с учетом блочно-криволинейной анизотропиии и ползучести. Предлагается разработанное программное обеспечение на базе Научно-образовательного центра «Суперкомпьютерное инженерное моделирование и разработка программных комплексов» МГТУ им. Н.Э. Баумана для создания, описания, решения, анализа моделей грунта и других математических моделей.
Ключевые слова: горная порода, напряженно-деформированное состояние, уравнения ползучести, анизотропия, численные методы, метод конечных элементов.
SOLUTION TO THE PROBLEM OF CREEP OF CURVILINEAR-ANISOTROPIC MEDIA BY THE RUNGE-KUTTA-FEHLBERG METHOD OF 5-6 ORDER
Научная статья
Dimitrienko Yu.I.1,Yurin Yu.V.2, Gumirgaliev T.R.3, Krasnov G.A.4, *
4 ORCID: 0000-0002-4577-9922;
1, 2, 3, 4 Bauman Moscow State Technical University, Moscow, Russia
* Corresponding author (krasnov14107[at]mail.ru)
Abstract
The article proposes a method for preliminary analysis of the composition and assessment of the dynamics of layers of deep-lying rock formations, physical knowledge of which is insufficient or cannot be obtained experimentally without the stage of development and launch of wells, mines and quarries. This method is based on modeling the stress-strain state of rocks taking into account block-curved anisotropy and creep. The paper proposes a method for an effective numerical solution of the stress-strain state problem taking into account block-curved anisotropy and creep. The developed software is offered on the basis of the Scientific and Educational Center "Supercomputer engineering modeling and development of software complexes" of the Bauman Moscow State Technical University to create, describe, solve, analyze soil models and other mathematical models.
Keywords: rock, stress-strain state, creep equations, anisotropy, numerical methods, finite element method.
Введение
В области поиска полезных ископаемых существует значительное количество проблем, связанных с предварительным моделированием и анализом местности, в которой проводятся геолого-разведывательные операции. Одной из самых значительных задач является расчет напряженно-деформированного состояния пород глубокого залегания, знание о которых быстрыми и экономически не затратными способами не может быть получено. Для работ, связанных с моделированием горных пород глубокого залегания требуется понимать характер и картину слоев грунта. Для этого проводится комплекс взрывных мероприятий с использованием тринитротоллуоловых шашек, которые помещаются на необходимые глубины под землю и полученные данные сейсморазведки заносятся в файл. Таких данных, порой, бывает достаточно для того, чтобы определить где стоит производить поисковые мероприятия по добыче полезных ископаемых, но существуют сложные разновидности рельефа и почвы, при которых однозначный ответ на поиск ископаемых дать нельзя. Для таких случаев используется процесс моделирования слоев горных пород, расчет напряженно-деформированного состояния слоев с целью определения состава и динамики этих пород, а также их анализ на предмет содержания веществ со свойствами нефти, газа, угля, прочих скоплений драгоценных материалов или со свойствами похожими на свойства перечисленных полезных ископаемых.
В работе создается геометрическая модель по данным 3-мерной сейсмической миграции. В полученной геометрии выделяются криволинейные блоки с помощью диаграммы Вороного. На полученной геометрии строится тетраэдральная сетка с квадратичной аппроксимацией. С помощью метода конечных элементов, решается задача НДС и находятся перемещения и напряжения, возникающие при давлении на блок горной породы с его граней.
Более подробную информацию по теме данной работы можно изучить в источниках [1], [16].
Концептуальная постановка задачи
Цель — Разработать или использовать существующие численные методы решения систем нелинейных алгебраических уравнений, а также решить задачу напряженно-деформированного состояния горных пород, разбитых на криволинейные кластеры с индивидуальными свойствами трансверсально-изотропного материала и ползучестью в автоматизированном программном комплексе (далее АПК) программ GeoPhysicsCAD, SMCM, разработанных в НОЦ «СИМПЛЕКС» МГТУ им. Н.Э. Баумана.
Задачи:
- Провести расчет напряженно-деформированного состояния горных пород с учетом блочно-криволинейной анизотропии и ползучести методом РКФ - 56 с адаптивным шагом;
- Провести анализ результатов решения задачи НДС, определить напряженно-деформированную картину пластов горных пород и оценить их динамику, проанализировать прирост производительности в решении задачи НДС.
Математическая постановка задачи
Рассмотрим краевую трехмерную задачу с условием ползучести: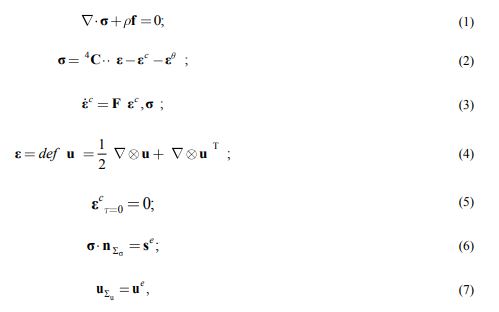 где: (1) — уравнение равновесия сплошной среды; (2) — определяющие соотношения с учетом деформаций ползучести; (3) — соотношения для деформаций ползучести; (4) — соотношение Коши; (5) — начальное условие; (6), (7) — граничные условия; здесь использованы обозначения:
где: (1) — уравнение равновесия сплошной среды; (2) — определяющие соотношения с учетом деформаций ползучести; (3) — соотношения для деформаций ползучести; (4) — соотношение Коши; (5) — начальное условие; (6), (7) — граничные условия; здесь использованы обозначения: Блочно-криволинейная анизотропия и ползучесть
Рассмотрим краевую трехмерную задачу (1)—(7).
Вектор напряжений se на границе блока горной породы, задающий тектонические напряжения, представим линейно изменяющимся с глубиной горной породы:
| (8) |
n — векторнормали к границе блока.
Слои горной породы будем считать анизотропными, а именно — трансверсально-изотропными.
Матрица коэффициентов податливости для трансверсально-изотропного тела:
E1 — модуль упругости в плоскости изотропии;
E2 — модуль упругости в направлении, перпендикулярном плоскости изотропии;
G2— модуль сдвига в плоскостях, перпендикулярных плоскости изотропии;
m1, m2— коэффициенты Пуассона, характеризующие сокращения соответственно в плоскости изотропии и в направлении, перпендикулярном этой плоскости, при растяжении в плоскости изотропии [12].
В трансверсально-изотропном теле все направления в плоскости изотропии и направление, перпендикулярное этой плоскости, являются главными направлениями упругости. Поэтому для такого тела главные оси деформированного состояния совпадают с главными осями напряженного состояния, если одна из главных осей напряженного состояния перпендикулярна плоскости изотропии.
Рассмотрим тензоры модулей упругостиСимметричный тензор модулей упругости ![]() для трансверсально-изотропного тела с плоскостью симметрии свойств X1, X2 выглядит следующим образом:
для трансверсально-изотропного тела с плоскостью симметрии свойств X1, X2 выглядит следующим образом:
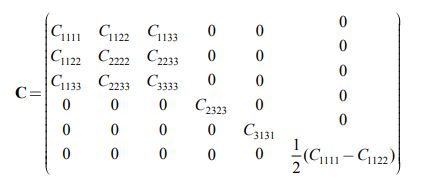 |
(12) |
Матрица коэффициентов теплового расширения ![]() для трансверсально изотропного тела:
для трансверсально изотропного тела:
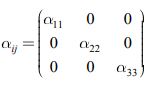 |
(13) |
Выражениями (12), (13) представлен материал с гексагональной симметрией, в которой свойства тела не зависят от поворота системы вокруг оси X , то есть при следующем преобразовании координат:![]()
![]()
Трансверсально-изотропный материал обладает пятью независимыми константами для тензора ![]() (см. (12)) и двумя константами для тензора
(см. (12)) и двумя константами для тензора ![]() (см. (13)) [7].
(см. (13)) [7].
Горная порода, исследуемая в работе, в рамках компьютерной 3D-модели была разделена на шесть типов областей, которые на основании информации об их продольных и поперечных скоростях звука были классифицированы как:
1) сланец песчанистый;
2) известняк;
3) песчаник крупнозернистый;
4) песчаник мелкозернистый;
5) алевролит;
6) галит.
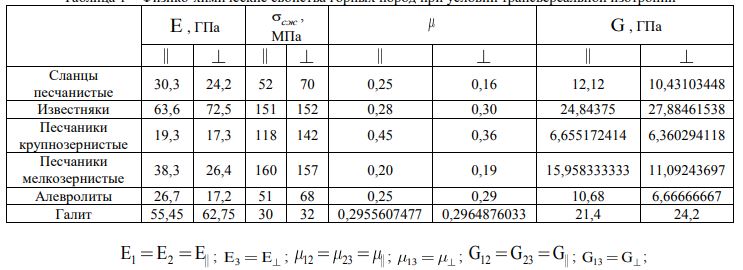
Свойства материалов, рассматриваемых в работе, приведены в таблице 1. Свойства одинаковые в плоскости, параллельной плоскости изотропии C1, C2.
Таблица была составлена, используя источники [2], [5], [6], [7], [9], [13] и др.
Таблица 1 – Физико-химические свойства горных пород при условии трансверсальной изотропии
где![]() — значения модулей сдвига при деформировании в плоскости напластования и по нормали к плоскости напластования соответственно [14].
— значения модулей сдвига при деформировании в плоскости напластования и по нормали к плоскости напластования соответственно [14].
Явный метод Рунге — Кутта — Фельберга 5-6 порядка
При интегрировании данным методом на каждом шаге рассчитываются 7 промежуточных точек – в нашем случае решается 7 задач на нахождение тензоров деформаций и напряжений . Реализация метода предполагает построение неравенства для контроля точности вычислений, которое при правильном выборе погрешности не приводит к дополнительным вычислительным затратам.
Для системы дифференциальных уравнений:
| |
(14) |
Для тензоров и на начальном шаге, учитывая условие (21), имеем:
- Вычисление тензора напряжений:
| |
(26) |
При выборе допустимой погрешности метода следует учесть вероятность непредсказуемого возрастания накопленной ошибки. Точность можно увеличить с помощью специальных способов отображения чисел в памяти компьютера. Следует заметить, что данный алгоритм считается одним из лучших среди методов типа Рунге — Кутта 6-го порядка точности [3].
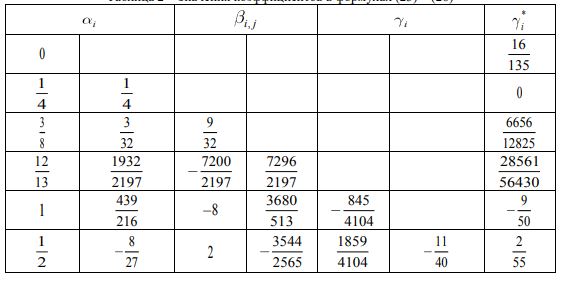
Значения всех коэффициентов приведены в таблице 2:
Таблица 2 – Значения коэффициентов в формулах (23) – (26)
Сравнительный анализ результатов при решении задачи НДС балки аналитически, явным методом Эйлера и методом РКФ – 5-6
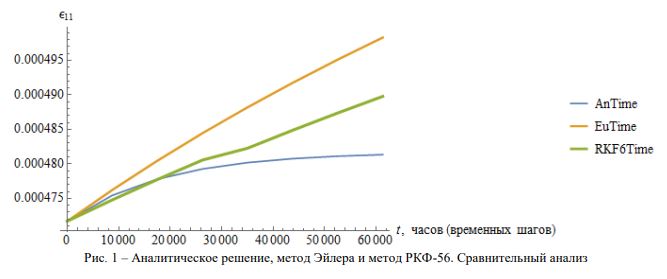
На рисунке 1 приведены графики, показывающие как значение компоненты e11 тензора деформаций e изменяется от количества временных шагов. Видно, что численное решение методом Рунге — Кутта — Фельберга 5-6 порядка располагается ближе к аналитическому решению, чем решение методом Эйлера.
Рис. 1 – Аналитическое решение, метод Эйлера и метод РКФ-56. Сравнительный анализ
Функция ползучести горных пород
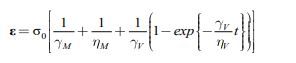 |
(27) |
где y и n — модуль упругости и коэффициенты вязкости; индексы M и V относятся к моделям Максвелла и Войгта.
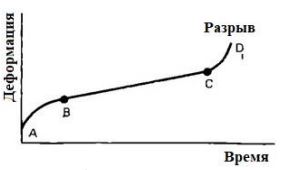
Пока t мало, это уравнение может выражать первичную ползучесть (или переходную ползучесть). При t=o это уравнение выражает упругую деформацию в видеНа рисунке 2 представлен график кривых ползучести.
Рис. 2 — Кривые ползучести:
АВ – первичной; ВС – вторичной;CD – третичной
Метод конечных элементов для решения задачи НДС горных пород
Рассмотрим краевую задачу (1) — (7) и тензор напряжений ![]()
Предполагаем, что тензор модулей упругости 4C удовлетворяет условию положительной определенности — для всякого симметричного тензора второго ранга справедливо неравенство:
| |
(28) |
Производим переход к матричной записи задачи. Для этого записываем компоненты соответствующих тензоров и векторов в декартовых координатах:
Преобразуя интегральное соотношение (33) с учетом (34), (35), (36) и (37), и, раскладывая каждый из интегралов этого соотношения по всей областиСетка из конечных элементов (далее КЭ) содержит в себе 1875293 тетраэдров и 328847 узлов. Каждый тетраэдр рассматривается с квадратичной аппроксимацией — десятиузловой тетраэдр.
Результаты численного моделирования
На данном рисунке представлены диаграммы компонент тензора qs напряжений кластеров горной породы и видна динамика изменений компонент напряжений в зависимости от направления осей ортонормированных базисов анизотропии.
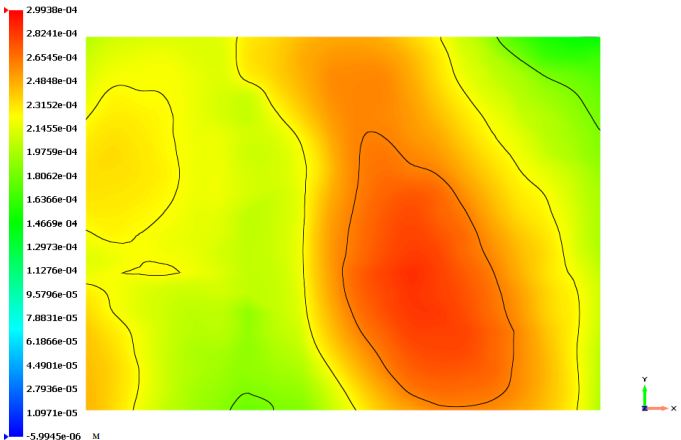 Рис. 3 – 3D Диаграмма перемещений по оси OZ на верхней поверхности
Рис. 3 – 3D Диаграмма перемещений по оси OZ на верхней поверхности
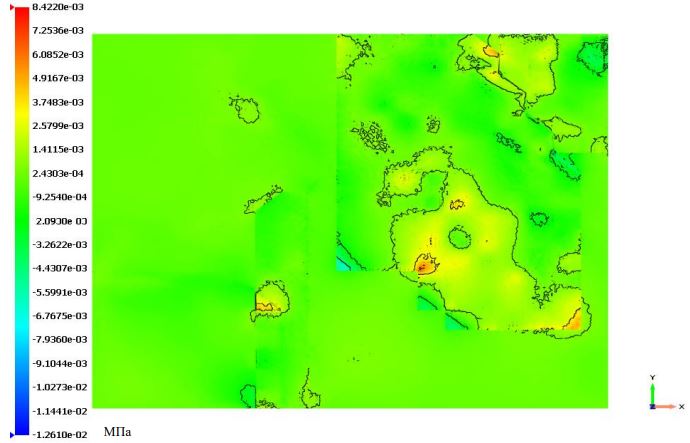 Рис. 4 – 3D Диаграмма сдвиговых напряжений в плоскости XY в собственной СК на верхней поверхности
Рис. 4 – 3D Диаграмма сдвиговых напряжений в плоскости XY в собственной СК на верхней поверхности
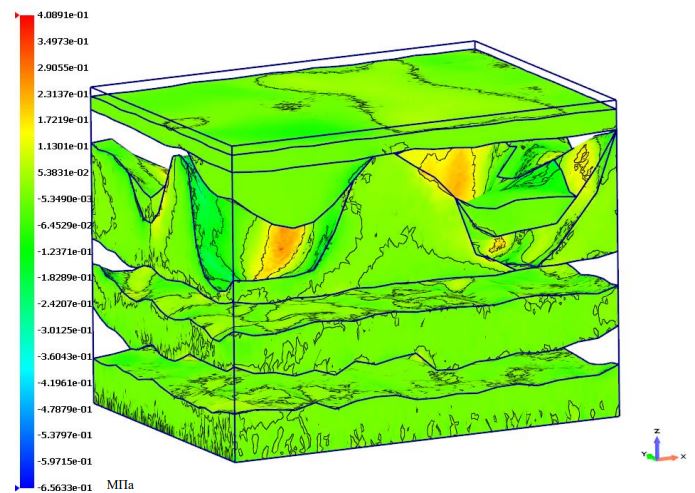 Рис. 5 – 3D Диаграмма сдвиговых напряжений в плоскости XY в собственной СК
Рис. 5 – 3D Диаграмма сдвиговых напряжений в плоскости XY в собственной СК
Заключение
Можно сказать, что, применяя метод РКФ-56 порядка, получилось добиться ускорения решения задачи НДС на 29% для достижения необходимой точности решения, а также уменьшения количества итераций алгоритма в 3.2 раза. Следует заметить, что при решении данной задачи устанавливается условие для точности решения и количество временных шагов формируется для каждого численного алгоритма автоматически исходя из этого условия – с какой невязкой будет решаться задача, если она устойчива и обладает всеми необходимыми начальными и граничными условиями для решения.
На рисунках 3 – 5 представлены диаграммы НДС горной породы, по которым можно сказать как перемещаются пласты породы в зависимости от действующих на них сил и давлений с течением времени, другими словами, оценить динамику и характер напластования горных слоев.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Dimitrienko Yu I Creep Deformations of Curvilinear Anisotropic Media: Finite Element Modeling / Yu I Dimitrienko, Yu V Yurin, T R Gumirgaliev et al. //IOP Journal of Physics: Conference Series1990, 2021. – 8 p.
- Димитриенко Ю.И. Конечно-элементное моделирование напряженно-деформируемого состояния горных пород с учетом ползучести/ Ю.И. Димитриенко, Ю.В. Юрин // Математическое моделирование и численные методы. – М.:МГТУ им. Н.Э. Баумана, 2015, №3, с. 101 –118
- Корягин С.В. Сравнительный анализ методов интегрирования с плавающим шагом/С.В. Корягин, А.А. Яковлев. – М.:CloudofScience, 2016, T.3, №1, – с. 95 – 103
- Димитриенко Ю.И. Универсальные законы механики и электродинамики сплошных сред / Ю.И. Димитриенко. – М.: МГТУ им. Н.Э. Баумана, 2011. – 560 с.
- Гзовский М.В. Основы тектонофизики / М.В. Гзовский. – М.: НАУКА, 1975. – 537 с.
- Ташкинов А.А. Упругость анизотропных материалов. Конспект лекций / А.А. Ташкинов. – 2010. – 49 с.
- Димитриенко Ю.И. Механика сплошной среды. В 4 т. Т. 4: Основы механики твердого тела / Ю.И. Димитриенко. – М.: МГТУ им. Н.Э. Баумана, 2013. – 624 с;
- Зенкевич О. Конечные элементы и аппроксимация / О. Зенкевич, К. Морган. – М.: МИР, 1986. – 320 с.
- Ребецкий Ю.Л. Механизм генерации остаточных напряжений и больших горизонтальных сжимающих напряжений в земной коре внутриплитовых орогенов. Проблемы тектонофизики / Ю.Л. Ребецкий. – М.: ИФЗ РАН, 2008. – с. 431 – 466.
- Скворцов Ю.В. Механика композиционных материалов / Ю.В. Скворцов. – С.: СГАУ им. ак. С.П. Королёва, 2013. – 94 с.
- Карабцев С.Н. Построение диаграммы Вороного и определение границ области в методе естественных соседей / С.Н. Карабцев, С.В. Стуколов. – К.: ИВТ Сибирского отделения РАН, 2008, №3, с. 65 – 80.
- Лехницкий С.Г. Теория упругости анизотропного тела / С.Г. Лехницкий. – М.: Изд. Технико-теоретическойлитературы, 1950. – 300 с.
- Aptukov V. N. Nano-range mechanical characterictics of carnallite, spathic salt and sylvite / V N Aptukov , V Yu Mitin, N E Moloshtanova et al. // Journal of Mining Science 49(3), 2013. –P. 382–387.
- Баклашов И.В. Геомеханика том 2. Геомеханические процессы / И.В. Баклашов, Б.А. Картозия, А.Н. Шашенко, В.Н. Борисов. – М.: Изд. МГГУ, 2004. – 249 с.
- Сегерлинд Л. Применение метода конечных элементов / Л. Сегерлинд. – М.: МИР, 1979. – 390 с.
- Dimitrienko Yu. I. Universal models for effective constitutive relations of laminated composites with finite strains / Yu.I. Dimitrienko, E.A. Gubareva, S.B. Karimov et al. //IOP Journal of Physics: Conference Series 1141(1),2018. – P. 72–93.
Список литературы на английском языке / References in English
- Dimitrienko Yu I Konechno-jelementnoe modelirovanie deformacij polzuchesti krivolinejno-anizotropnyh sred [Creep Deformations of Curvilinear Anisotropic Media: Finite Element Modeling] / Yu I Dimitrienko, Yu V Yurin, T R Gumirgaliev et al. //IOP Journal of Physics: Conference Series1990, 2021. – 8 p.
- Dimitrienko Yu I Konechno-jelementnoe modelirovanie naprjazhenno-deformiruemogo sostojanija gornyh porod s uchetom polzuchesti [Finite element modeling of the intense deformed condition of rocks taking into account creep] / Yu I Dimitrienko, Yu V Yurin. // Matematicheskoe modelirovanie i chislennye metody [Mathematical modeling and Computational methods].3, 2015. – P. 101–118. [in Russian]
- Koryagin S V Sravnitel'nyj analiz metodov integrirovanija s plavajushhim shagom [Comparative analysis of integration methods with a floating step] / S V Koryagin, A A Yakovlev // Cloud of science3(1), 2016. –P. 95–103. [in Russian]
- Dimitrienko Yu I Universal'nye zakony mehaniki i jelektrodinamiki sploshnyh sred [Universal laws of mechanics and electrodynamics of continuous media] / Yu I Dimitrienko. – M: Bauman Moscow State Technical University Publ, 2011. – 560 p. [in Russian]
- Gzovsky M V Osnovy tektonofiziki [Fundamentals of tectonophysics] / M V Gzovsky. – M: SCIENCE Publ., 1975. – 537 p. [in Russian]
- Tashkinov A A Uprugost' anizotropnyh materialov. Konspekt lekcij [Elasticity of anisotropic materials (Lecture)] / A A Tashkinov. – 2010. – 49 p. [in Russian]
- Dimitrienko Yu I Mehanika sploshnoj sredy: Osnovy mehaniki tverdogo tela [Continuum mechanics vol. 4. Fundamentals of solid mechanics] / Yu I Dimitrienko. – M: Bauman Moscow State Technical University Publ., 2013. – 624 p. [in Russian]
- Zenkevich O Konechnye jelementy i approksimacija [Finite elements and approximation] / O Zenkevich, K Morgan. –Moscow: MIR Publ., 1986. – 320 p. [in Russian]
- Rebetsky Yu L Mehanizm generacii ostatochnyh naprjazhenij i bol'shih gorizontal'nyh szhimajushhih naprjazhenij v zemnoj kore vnutriplitovyh orogenov. Problemy tektonofiziki [The mechanism of generation of residual stresses and large horizontal compressive stresses in the earth’s crust of intraplate orogens. Problems of tectonophysics] / Yu L Rebetsky. –Moscow: IPE RAS., 2008. – P. 431–466. [in Russian]
- Skvortsov Yu V Mehanika kompozicionnyh materialov [Mechanics of composite materials] / Yu V Skvortsov. –Samara: SSAU im. ac. S P Koroleva Publ., 2013. – 94 p. [in Russian]
- Karabtsev S N Postroenie diagrammy Voronogo i opredelenie granic oblasti v metode estestvennyh sosedej [Construction of a Voronoi diagram and determination of the boundaries of the region in the method of natural neighbors] / S N Karabtsev, S V Stukolov. –Novosibirsk: ICT SB RAS Publ.3, 2008. – P. 65–80. [in Russian]
- Lekhnitskiy S G Teorija uprugosti anizotropnogo tela [The theory of elasticity of an anisotropic body] / S G Lekhnitskiy. –Moscow: Techno-theoretical literature Publ., 1950. – 300 p. [in Russian]
- Aptukov V. N. Nano-range mechanical characterictics of carnallite, spathic salt and sylvite / V N Aptukov , V Yu Mitin, N E Moloshtanova et al. // Journal of Mining Science 49(3), 2013. –P. 382–387.
- Baklashov I V Geomehanika. Geomehanicheskie processy [Geomechanics vol. 2. Geomechanical processes] / I V Baklashov, B A Kartozia, A N Shashenko et al. –Moscow: MGGU Publ., 2004. – 249 p. [in Russian]
- Segerlind L Primenenie metoda konechnyh jelementov [Application of the finite element method] / L Segerlind. –Moscow: MIR Publ., 1979. – 390 p. [in Russian]
- Dimitrienko Yu. I. Universal models for effective constitutive relations of laminated composites with finite strains / Yu.I. Dimitrienko, E.A. Gubareva, S.B. Karimov et al. //IOP Journal of Physics: Conference Series 1141(1),2018. – P. 72–93.