РАСЧЁТ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ БЕСКОНТАКТНОГО ДВИГАТЕЛЯ С ПОСТОЯННЫМИ МАГНИТАМИ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ

РАСЧЁТ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ БЕСКОНТАКТНОГО ДВИГАТЕЛЯ С ПОСТОЯННЫМИ МАГНИТАМИ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ

Научная статья

Андросов Н.Н.¹, Низовой А.Н.²

^{1, 2}НОУ ВПО «Международный институт компьютерных технологий», Воронеж, Россия

Аннотация

В статье рассматривается задача математического расчета электромагнитного поля бесконтактного двигателя с постоянными магнитами (БДПМ) методом конечных элементов, представлен порядок создания и реализации конечно-элементных моделей. Использование предложенного подхода к проектированию сокращает затраты времени и позволяет решить задачу без создания и испытаний большого количества разных образцов БДПМ, а также сократить затраты на изготовление технологической оснастки.

Ключевые слова: метод конечных элементов , проектирование.

Key words: method final element , designing.

В основе расчета электромагнитного поля бесконтактного двигателя с постоянными магнитами (БДПМ) методом конечных элементов (МКЭ) лежит система уравнений Максвелла. В ходе решения МКЭ эти уравнения реализуются численно, при этом операции над величинами в процессе расчетов производятся с матрицами, соответственно этому и записаны все выражения:

(1)

(2)

(3)

(4)

где  – ротор векторного поля (векторное произведение оператора Гамильтона на вектор);

–  дивергенция  векторного поля (скалярное произведение оператора Гамильтона на вектор);

–   вектор напряженности магнитного поля;

–   вектор, соответствующий полной плотности тока;

–   вектор, соответствующий плотности тока проводимости;

–   вектор, соответствующий плотности тока смещения;

–   вектор, соответствующий плотности тока, возникающего при движении (переноса);

–   вектор электрического смещения;

–   время;

–   вектор напряженности электрического поля;

–   вектор магнитной индукции;

–   объемная плотность электрического заряда.

Из уравнения (1) после применения оператора дивергенции получается выражение:

.                                                                 (5)

В соответствии с последним выражением, для того, чтобы рассчитать картину электромагнитного поля, в качестве нагрузки следует задавать плотность тока, а точнее – плотность тока проводимости .

Уравнения (1)-(4) дополняются выражениями, которые описывают электромагнитные свойства материалов. Для всех материалов, кроме постоянных магнитов, характеристики намагничивания описывается зависимостями вида:

,                                                                                 (6)

где – матрица абсолютных магнитных проницаемостей, выражающая зависимость индукции от напряженности магнитного поля.

В случае наличия постоянных магнитов используется выражение:

,                                                      (7)

где  – магнитная постоянная (магнитная проницаемость вакуума);

– т. н. вектор остаточной внутренней намагниченности материала.

Используя понятие удельного магнитного сопротивления, можно записать выражение (7) иначе:

(8)

где  – матрица удельного магнитного сопротивления, равная ;

– удельное  магнитное сопротивление вакуума, равное .

Аналогичное выражение можно записать и для электрического поля:

;                                                (9)

,                                                                                   (10)

где – матрица удельных проводимостей;

;                                                                   (11)

– матрица диэлектрических проницаемостей;

;                                                                                    (12)

– вектор скоростей;

.                                                                                                            (13)

Решение  уравнений магнитного поля в общем случае достигается с использованием потенциальных функций. Различают две формулировки задачи с использованием потенциальных функций: на основе понятия магнитного векторного потенциала (MVP formulation), либо на основе магнитного скалярного потенциала (MSP formulation). Применять то или другое зависит от характера изменения поля во времени, рассмотрения задачи в двумерной (2D) или трехмерной (3D) постановке, того, как задаются источники тока, от размеров рассматриваемой области и степени дискретизации.

Подход, основанный на использовании магнитного скалярного потенциала, используется только в случае трехмерного анализа (3D). Подход, основанный на использовании магнитного векторного потенциала, применяется как при двумерном, так и при трехмерном анализе. В данной работе используется двумерный анализ.

При составлении уравнений электромагнитного поля для электрической машины, как правило, делаются следующие допущения [1,2, 3,4]:

1. Величина ЭДС электромагнитной индукции несоизмеримо больше любых других ЭДС, например: контактной, Холла, Томпсона и т. д., в связи с чем, последними пренебрегают.
2. Пренебрежимо малы по сравнению с токами проводимости в проводниках: а) токи проводимости в диэлектриках; б) конвекционные токи, возникающие при движении зарядов вместе со средой, в связи с чем последними пренебрегаем.

Так как токи проводимости, смещения и конвекционные в диэлектрике, заполняющем зазор между частями статора и ротора, не учитываются, скорость перемещения диэлектрика (газа или жидкости) в зазоре не оказывает влияния на электромагнитное поле.

3. Пренебрежимо малы токи смещения и запаздывание в распространении электромагнитных волн в пределах области поля, что позволяет считать электромагнитное поле в машине квазистационарным (в [1] А. В. Иванов-Смоленский показал, что условия квазистационарности электромагнитного поля в электрической машине соблюдаются).
4. При рассмотрении поля в неферромагнитной среде относительная магнитная проницаемость этой среды принимается равной единице.

С учетом приведенных допущений, а также отсутствием свободных зарядов, уравнения  (1)-(4) принимают вид:

(14)

(15)

(16)

Решение может быть найдено, если ввести понятие векторного магнитного потенциала, который позволяет описать магнитное поле (B) и электрическое (E) в виде выражений:

,                                                                                                       (17)

,                                                                                   (18)

где  – векторный магнитный потенциал;

– электрический скалярный потенциал.

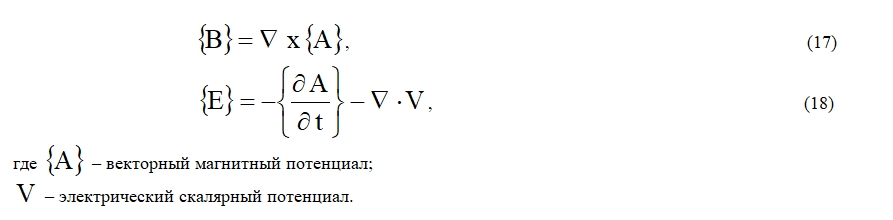
Таким образом, получены выражения, представляющие собой систему проектирования бесконтактных двигателей с постоянными магнитами (БДПМ) методом конечных элементов, предложенный подход к проектированию сокращает затраты времени и позволяет решить задачу без создания и испытаний большого количества разных образцов БДПМ, а также сократить затраты на изготовление технологической оснастки.