ПОПЕРЕЧНЫЕ ВОЛНЫ В НЕУПРУГОЙ НИТИ
ПОПЕРЕЧНЫЕ ВОЛНЫ В НЕУПРУГОЙ НИТИ
Научная статья
Комаров А.Д.
Московский физико-технический институт, Москва, Россия
Аннотация
В работе показывается, что в основе поперечных волн лежит явление качения, когда линейное смещение и поворот неотделимы.
Возьмем гибкую нерастяжимую нить, при помощи которой во всех курсах физики начинается знакомство с волновыми явлениями, но вместо традиционного «малого» возмущения, рассмотрим возмущение в виде плоской кольцеобразной петли, катящейся вдоль нити. Пусть Т - натяжение нити, μ- линейная плотность, гравитация отсутствует. Толщина нити только для понятности рисунка.
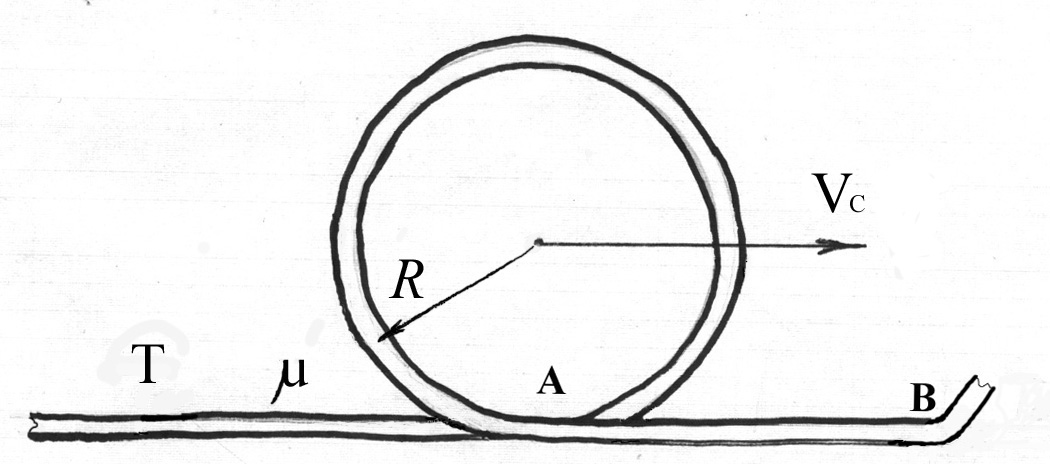
Рис 1. Катящееся кольцо из гибкой нерастяжимой нити.
Такое возмущение может существовать лишь при скорости петли относительно нити 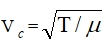 , когда натяжение нити в любой точке петли становится равным натяжению вне петли.
, когда натяжение нити в любой точке петли становится равным натяжению вне петли.
Самый простой и эффективный способ исследования возмущений в гибкой нити заключается в обращении движения. Достаточно рассмотреть вращающийся шкив, который охватывает при своем движении гибкая нерастяжимая нить, и найти ту скорость, при которой нить перестает взаимодействовать с опорой. Интересно, что скорость Vc не зависит ни от радиуса шкива, ни от угла охвата, что позволяет предположить о возможности построения произвольного плоского контура (даже замкнутого и вечного») из нити, движущейся со скоростью Vc. Это явление известно под названием эффекта Эткина-Радингера [1].
К сожалению, в большинстве учебников к распространению поперечных возмущений в нерастяжимой бесконечной нити подходят, как к распространению поперечных колебаний, порождаемых силами упругости. Такой подход не может считаться корректным. В отрезке нити, зажатом с концов, можно говорить о колебаниях и силах упругости, стремящихся вернуть струну в начальное состояние. Но неправильно говорить о «поперечных волнах упругости» в бесконечной нити, в бесконечной нерастяжимой нити нет поперечных сил упругости. Пример с катящимся кольцом говорит, что в волне должны присутствовать два вида энергии – вращательная и энергия поступательного движения, подобно электрической и магнитной составляющим в электромагнитном возмущении. Для каждого вида энергии действуют свои законы сохранения. Периодической перекачки энергии из одного вида в другой, как при колебаниях, не происходит.
Перемещение поперечных возмущений вдоль нерастяжимой нити – типичная волна. Скорость 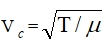 - это скорость поперечных волн в нити.
- это скорость поперечных волн в нити.
Движение волновое, если оно описывается функцией вида U=U(x±ct), которая всегда удовлетворяет волновому уравнению ²U/x²=(1/c²)·²U/t² .
На рис.2 показан участок нити, движущейся со скоростью V вправо вдоль оси x.
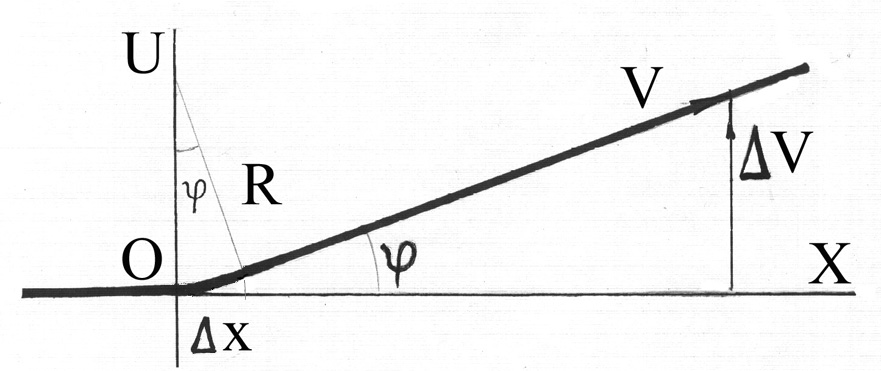
Рис.2 Изменение направления движения нити на угол φ
В начале координат нить за время Δt изменяет направление движения на угол φ и приобретает составляющую скорости ΔV в направлении оси U. Считая угол φ малым, и учитывая, что V= dx/dt=const , можно записать очевидные соотношения:
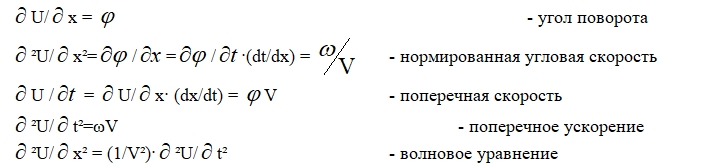
Волновое уравнение в данном случае имеет простой смысл: поперечное ускорение элемента нити пропорционально угловой скорости этого элемента. Коэффициент пропорциональности равен продольной скорости нити.
Масса участка нити, изменившей свое направление за время Δt , равна
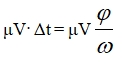
Приравнивая произведение массы 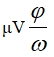 на ускорение ωV к величине вертикальной составляющей силы φТ , можно получить уравнение для определения скорости Vc, при которой нить не должна взаимодействовать с опорой.
на ускорение ωV к величине вертикальной составляющей силы φТ , можно получить уравнение для определения скорости Vc, при которой нить не должна взаимодействовать с опорой.
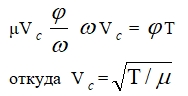
Поскольку нить не взаимодействует с опорой, то остается допустить, что изменение направления движения происходит за счет внутренней, уже имеющейся в нити энергии вращения. Эта энергия легко вычисляется, если учесть, что энергия вращения полного кольца при скорости качения Vc равна πRT. Участок кольца с углом поворота φ обладает запасом энергии вращения 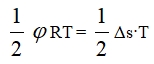 , где Δs длина участка нити, обладающего энергией вращения. Этот же участок имеет импульс вдоль оси U , равный p = Tφ Δt = T/R Δs и момент импульса L=TR Δt = T/ω Δs . Причем этот участок с «вращением» смещается относительно нити влево (на рис.2) со скоростью
, где Δs длина участка нити, обладающего энергией вращения. Этот же участок имеет импульс вдоль оси U , равный p = Tφ Δt = T/R Δs и момент импульса L=TR Δt = T/ω Δs . Причем этот участок с «вращением» смещается относительно нити влево (на рис.2) со скоростью 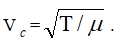
В результате можно утверждать, что распространение возмущений в нити связано с распространением «вращательного» возмущения. То есть вдоль нити смещается момент количества движения и обязательно сопутствующее ему количество поперечного движения. Наиболее близко к описанию данного процесса подходит термин качение, который свидетельствует о неотделимости смещения от поворота. Нельзя сместить нить поперек, не придав ей угла поворота, и нельзя повернуть нить без поперечного смещения. Это чисто кинематическая связь, подобная связи вращения катящегося обруча с его поступательным движением V=ωR . Волновое уравнение – кинематическое уравнение.
Поэтому правильнее говорить о волнах качения или о катящихся волнах в нити.
На рис.3 нарисована треугольная волна, двигающаяся справа налево .
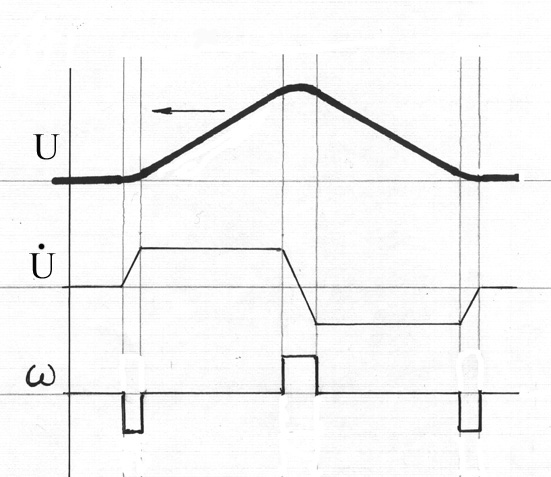
Рис.3 Треугольная волна
Для простоты все углы имеют одинаковый радиус R. Нижний левый угол соответствует схеме на рис.2. Под волной изображены диаграммы вертикальной составляющей скорости и угловой скорости. Понятно, что треугольная волна образуется тремя «катящимися» вдоль нити «вращательными» возмущениями, каждое со своей энергией.
И самое интересное. Из рис.1 можно сделать замечательный вывод. Если очень ловко и быстро разрезать петлю в точке А и склеить отдельно детали кольца и покоящейся нити, то кольцо будет катиться вдоль нити вплоть до точки В, где пути кольца и нити разойдутся. Произойдет «излучение». Другими словами, замкнутая кольцевая петля, катящаяся со скоростью Vc, может существовать независимо от породившей ее нити.
Список литературы / References
- Меркин Д.Р. Введение в механику гибкой нити. – Москва: Наука, 1980
- Сивухин Д.В. Общий курс физики в 5т. Т.1 Механика. Изд. МФТИ. 2004
