ПОЛЬЗОВАТЕЛЬСКИЕ ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ ОДУ 1-ГО ПОРЯДКА
ПОЛЬЗОВАТЕЛЬСКИЕ ФУНКЦИИ VBA EXCEL ДЛЯ ЧИСЛЕННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ ОДУ 1-ГО ПОРЯДКА
Научная статья
Российский государственный университет туризма и сервиса, Пушкино, Россия
* Корреспондирующий автор (oasdv[at]yandex.ru)
АннотацияПриведены основные формулы приближенных решений задачи Коши обыкновенных дифференциальных уравнений 1-го порядка методами Эйлера, Адамса, в котором применяются конечные разности 1-го и 2-го порядка, и Рунге-Кутта четвертого порядка точности. Также приведены программные коды пользовательских функций VBA Excel, реализующие перечисленные методы. Данные пользовательские функции позволяют находить на компьютере в режиме онлайн приближенные решения задачи Коши для обыкновенных дифференциальных уравнений 1-го порядка. Все пользовательские функции имеют описания, поясняющие их назначения. Применение пользовательских функций показано на конкретных задачах, в том числе, когда решение надо найти на конечной последовательности равноотстоящих значений.
Ключевые слова: дифференциальное уравнение, задача Коши, приближенное решение, код, диалоговое окно.
CUSTOM EXCEL VBA FUNCTIONS FOR NUMERICAL SOLUTION OF A FIRST-ORDER CAUCHY ODE
Research article
Sdvizhkov O.A.*
Russian State University of Tourism and Service, Pushkino, Russia
* Corresponding author (oasdv[at]yandex.ru)
AbstractThe current study provides basic formulas for approximate solutions of a Cauchy problem of the first order ordinary differential equations by the methods of Euler, Adams, in which finite differences of the first and second-order, and Runge-Kutta of the fourth order are applied. The program codes of the VBA Excel custom functions that implement these methods are also provided. These custom functions allow finding approximate solutions to the Cauchy problem for the first order ordinary differential equations online. All custom functions have descriptions explaining their purpose. The use of custom functions is shown in solving specific problems, including when the solution must be found on a finite sequence of equidistant values.
Keywords: differential equation, a Cauchy problem, approximate solution, code, dialog box.
ВведениеМетоды приближенного решения задачи Коши обыкновенного дифференциального уравнения 1-го порядка, как известно [1], [2], [8], отличаются большой трудоемкостью. Поэтому, естественно, в информационных технологиях нужны инструменты, позволяющие выполнять эти вычисления автоматически.
Цель данного исследования – разработка на языке программирования VBA Excel [3], [4], [9] программных кодов пользовательских функций [5], которые находят приближенные решения задачи Коши обыкновенного дифференциального уравнения 1-го порядка в режиме онлайн методами Эйлера, Адамса и Рунге-Кутта. Как такие задачи решаются непосредственными вычислениями в Excel показано в [6].
Пользовательские функции VBA Excel [10] применяются в программировании численных методов решения ОДУ 1-го порядка впервые. Они позволяют пользователям Excel решать рассматриваемые задачи в режиме онлайн, заполняя диалоговые окна пользовательских функций.
- Пользовательская функция ЭЙЛЕР
Пусть создана пользовательская функция F, возвращающая f (x, y). Тогда на языке VBA Excel код пользовательской функции ЭЙЛЕР, выполняющей вычисления по формуле (1.2), имеет вид, приведенный в листинге 1.1.
Листинг 1.1. Код функции ЭЙЛЕР и ее описания
Function ЭЙЛЕР(Нач_x, Нач_y, Конеч_x, Шагов)
Dim n As Integer
n = Шагов
h = (Конеч_x - Нач_x) / n
ЭЙЛЕР = Нач_y
For i = 1 To n
ЭЙЛЕР = ЭЙЛЕР + F(Нач_x + h * (i - 1), ЭЙЛЕР) * h
Next
End Function
Sub InstallFunc1()
Application.MacroOptions Macro:="ЭЙЛЕР", Description:= _
"Возвращает у(x), x=Конеч_х, получаемое методом Эйлера"
End Sub
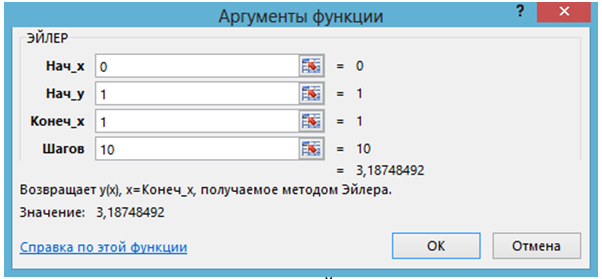
В [7] разбирается пример, в котором методом Эйлера надо найти приближенное решение при х = 1 задачи Коши
разбивая отрезок [0, 1] на 10 равных частей. Пусть создана пользовательская функция F, возвращающая f (x, y) = х + у, и пользовательская функция ЭЙЛЕР. Тогда онлайн-решение поставленной задачи имеет вид:
Рис. 1.1 – Применение функции ЭЙЛЕР в задаче (1.3) при х=1
Подробное решение с применением функции ЭЙЛЕР состоит в следующем.- В диапазон А1:К1 вводятся значения от 0 до 1 с шагом 0,1.
- В ячейку А2 вводится 1.
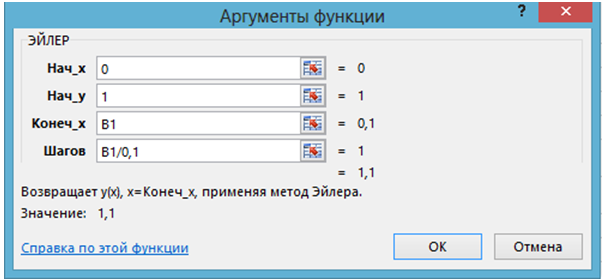
- Выделяется ячейка В2, вызывается функция ЭЙЛЕР и вводятся данные:
Рис. 1.2 – Применение функции ЭЙЛЕР со ссылками на ячейки
- Копирование формулы ячейки В2 в ячейки С2:К2 завершает решение задачи (рис. 1.3).
Рис. 1.3 – Результаты, возвращаемые функцией ЭЙЛЕР
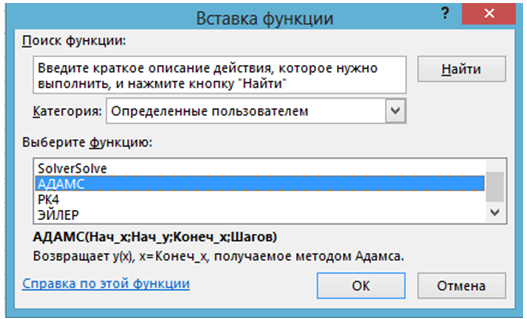
- Пользовательская функция АДАМС
В методе Адамса принимают:
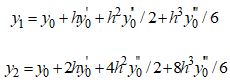 (2.1)
а каждое следующее значение yi вычисляют по формуле:
(2.1)
а каждое следующее значение yi вычисляют по формуле:
Пусть заданы пользовательские функции F, F1, F2, F11, F12, F22, возвращающие , соответственно. Тогда на языке VBA Excel код пользовательской функции АДАМС, выполняющей вычисления по формулам (2.1), (2.2), (2.3), записывается в виде, приведенном в листинге 2.1.
Листинг 2.1. Код функции АДАМС и ее описания
Function АДАМС(Нач_x, Нач_y, Конеч_x, Шагов)
Dim n As Integer
n = Шагов
Dim x(), y(), d(), del(), ddel()
ReDim x(0 To n), y(0 To n), d(0 To n)
x(0) = Нач_x
y(0) = Нач_y
h = (Конеч_x - x(0)) / n
d(0) = F(x(0), y(0))
s = F1(x(0), y(0)) + F2(x(0), y(0)) * d(0)
t = F11(x(0), y(0)) + 2 * F12(x(0), y(0)) * d(0) + F22(x(0), _ y(0)) * d(0) ^ 2 + F2(x(0), y(0)) * s
u = y(0) + d(0) * h + s / 2 * (h ^ 2) + t / 6 * (h ^ 3)
v = y(0) + d(0) * 2 * h + s / 2 * (2 * h) ^ 2 + t / 6 * _
(2 * h) ^ 3
Select Case n
Case 1
АДАМС = u
Case 2
АДАМС = v
Case Is >= 3
ReDim del(0 To n - 1), ddel(0 To n - 2)
For i = 1 To n
x(i) = x(0) + h * i
Next
y(1) = u: y(2) = v
For i = 3 To n
d(i - 2) = F(x(i - 2), y(i - 2))
d(i - 1) = F(x(i - 1), y(i - 1))
del(i - 3) = d(i - 2) - d(i - 3)
del(i - 2) = d(i - 1) - d(i - 2)
ddel(i - 3) = del(i - 2) - del(i - 3)
y(i) = y(i - 1) + d(i - 1) * h + del(i - 2) * h / 2 + _
ddel(i - 3) * 5 * h / 12
Next
АДАМС = y(n)
End Select
End Function
Sub InstallFunc2()
Application.MacroOptions Macro:="АДАМС", Description:= _
"Возвращает у(x), x=Конеч_х, получаемое методом Адамса"
End Sub
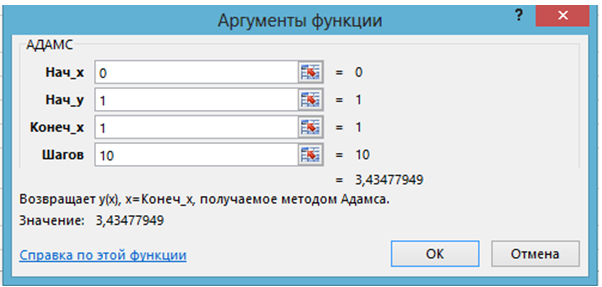
Онлайн-решение задачи (1.3) при х = 1 функцией АДАМС имеет вид:
Рис. 2.1 – Применение функции АДАМС в задаче (1.3) при х=1
Решение на отрезке [0, 1] задачи (1.3) функцией АДАМС показано на рисунке 2.2Рис. 2.2 – Результаты, возвращаемые функцией АДАМС
- Пользовательская функция РК4
В методе Рунге-Кутта четвертого порядка точности [1], [2], [7], которым численно решается задача Коши (1.1), применяется формула:
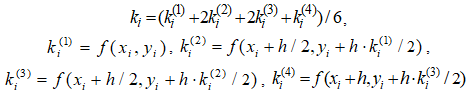 (3.2)
(3.2)
Пусть по правой части уравнения (1.1) создана пользовательская функция F, возвращающая f (x, y). Тогда код пользовательской функции РК4, выполняющей расчеты по формулам (3.1), (3.2), записывается в виде, приведенном в листинге 3.1.
Листинг 3.1. Код функции РК4 и ее описания
Function РК4(Нач_x, Нач_y, Конеч_x, Шагов)
Dim y(), k(1 To 4), n As Integer
n = Шагов
ReDim y(0 To n)
x0 = Нач_x: y(0) = Нач_y
h = (Конеч_x - x0) / n
For i = 1 To n
k(1) = F(x0 + (i - 1) * h, y(i - 1))
k(2) = F(x0 + (i - 1) * h + h / 2, y(i - 1) + h / 2 * k(1))
k(3) = F(x0 + (i - 1) * h + h / 2, y(i - 1) + h / 2 * k(2))
k(4) = F(x0 + (i - 1) * h + h, y(i - 1) + h * k(3))
y(i) = y(i - 1) + h / 6 * (k(1) + 2 * k(2) + 2 * k(3) + k(4))
Next
РК4 = y(n)
End Function
Sub InstallFunc3()
Application.MacroOptions Macro:="РК4", Description:= _
"Возвращает у(x), x=Конеч_х, получаемое методом Рунге-Кутта"
End Sub
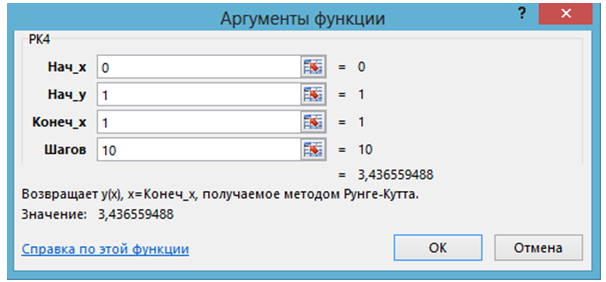
Пусть методом Рунге-Кутта требуется решить задачу (1.3) при х = 1. Тогда применение функции РК4 дает:
Рис. 3.1 – Применение функции РК4 в задаче (1.3) при х=1
Решение задачи (1.3) на отрезке [0, 1] функцией РК4 показано на рисунке 3.2.Рис. 3.2 – Результаты, возвращаемые функцией РК4
Следует заметить, что точное решение задачи (1.3) имеет вид:Рис. 3.3 – Вычисление у(1) в Excel
Поэтому абсолютная погрешность, с которой находится решение задачи (1.3) при х = 1 с помощью функции РК4, составляет менее 10-5.
Выводы- Применение пользовательских функций ЭЙЛЕР, АДАМС, РК4 не вызывает трудностей;
- Функции ЭЙЛЕР, АДАМС, РК4 позволяют самому широкому кругу пользователей ПК, каким является круг пользователей пакета Microsoft Office, численно решать задачи Коши для ОДУ 1-го порядка на компьютере в режиме онлайн;
- Функции ЭЙЛЕР, АДАМС, РК4, избавляющие от рутинных вычислений, будут полезны как в учебном процессе, так и в научных исследованиях, связанных с дифференциальными уравнениями 1-го порядка;
- Размещение листингов функций ЭЙЛЕР, АДАМС, РК4 в одной книге Excel превращают ее в калькулятор по численным методам решения задачи Коши для ОДУ 1-го порядка. Пользователю надо только выбирать и применять нужную функцию (рис. 4.1).
Рис. 4 – Меню пользовательских функций
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Бахвалов Н.С. Численные методы. / Н. С. Бахвалов. – М: Наука, 1975. – 632 с.
- Березин И.С. Методы вычислений, т. II. / И. С. Березин, Н. П. Жидков. – М.: ГИФМЛ, 1959. – 620 с.
- Гарнаев А.Ю. MS Excel 2002: разработка приложений. / А. Ю. Гарнаев. – СПб.: БХВ-Петербург, 2003. – 768 с.
- Джелен Б. Применение VBA и макросов в Microsoft Excel. : Пер. с англ. / Б. Джелен, Т. Сирстад. – М.: Издательский дом «Вильямс», 2006. – 624 с.
- Кузьменко В.Г. VBA 2003. / В. Г. Кузьменко – М: ООО «Бином-Пресс», 2004, 432 с.
- Ларсен Р.У. Инженерные расчеты в Excel: Пер. с англ. / Р. У. Ларсен. – М.: Издательский дом «Вильямс», 2002. – 544 с.
- Пискунов Н.С. Дифференциальное и интегральное исчисления. Для втузов, том второй. / Н. С. Пискунов. – М: Наука, 1970. – 576 с.
- Самарский А.А. Задачи и упражнения по численным методам: Учебное пособие. / А. А. Самарский, П. Н. Вабищевич, Е. А. Самарская. – М.: Эдиториал УРСС, 2000. – 208 с.
- Сдвижков О.А. Excel – VBA. Словарь-справочник пользователя / О. А. Сдвижков. – М.: Эксмо, 2008. – 224 с.
- Сдвижков О.А. DEcode (пользовательские функции) [Электронный ресурс]. – URL: https://oas.ucoz.com/load/odu_polzovatelskie_funkcii/1-1-0-35 (дата обращения: 20.01.2021)
Список литературы на английском языке / References in English
- Bakhvalov N. S. Chislennye metody [Numerical Methods] / N. S. Bakhvalov. – M: Nauka, 1975 – 632 p. [in Russian]
- Berezin I. S. Metody vychislenijj, t. II. [Methods of Calculations, vol. II] / I. S. Berezin, N. P. Zhidkov. – M.: GIFML, 1959 – 620 p. [in Russian]
- Garnaev A. Yu. MS Excel 2002: razrabotka prilozhenijj [MS Excel 2002: Application development] / A. Yu. Garnaev. – St. Petersburg: BKhV-Petersburg, 2003 – 768 p. [in Russian]
- Jelen B. Primenenie VBA i makrosov v Microsoft Excel [VBA and Macros: Microsoft Excel] Translation from English / B. Jelen, T. Sirstad. – M.: Williams, 2006 – 624 p. [in Russian]
- Kuzmenko V. G. VBA 2003 [VBA 2003] / V. G. Kuzmenko. – M: OOO "Binom-Press", 2004, 432 p. [in Russian]
- Larsen R. U. Inzhenernye raschety v Excel [Engineering with Excel] Translation from English / R. U. Larsen. – M.: Vilyams, 2002 – 544 p. [in Russian]
- Piskunov N. S. Differencial'noe i integral'noe ischislenija. Dlja vtuzov, tom vtorojj [Differential and Integral Calculus. For Higher Engineering Institutions, Volume II] / N. S. Piskunov. – M: Nauka, 1970. - 576 p. [in Russian]
- Samarsky A. A. Zadachi i uprazhnenija po chislennym metodam: Uchebnoe posobie [Problems and Exercises in Numerical Methods: A Textbook] / A. A. Samarsky, P. N. Vabishchevich, E. A. Samarskaya. – M.: Editorial URSS, 2000 – 208 p. [in Russian]
- Sdvizhkov O. A. Excel – VBA. Slovar'-spravochnik pol'zovatelja [Excel – VBA. Dictionary and User's Reference] / O. A. Sdvizhkov. – M.: Eksmo, 2008 – 224 p. [in Russian]
- Sdvizhkov O. A. DEcode (pol'zovatel'skie funkcii) [DEcode (custom functions)] [Electronic resource] / O. A. Sdvizhkov. – URL: https://oas.ucoz.com/load/odu_polzovatelskie_funkcii/1-1-0-35 (accessed: 20.01.2021) [in Russian]