ОПТИМИЗАЦИЯ КВАЗИЛИНЕЙНЫХ МОДЕЛЕЙ СИСТЕМ С ДВУМЯ СТРУКТУРАМИ И НЕЗАВИСИМЫМИ ПРИОРИТЕТАМИ
Красий Н.П.
Доцент, кандидат физико-математических наук, Донской государственный технический университет в г. Ростове-на-Дону
ОПТИМИЗАЦИЯ КВАЗИЛИНЕЙНЫХ МОДЕЛЕЙ СИСТЕМ С ДВУМЯ СТРУКТУРАМИ И НЕЗАВИСИМЫМИ ПРИОРИТЕТАМИ
Данная работа выполнена в рамках плана научных работ кафедры высшей математики ДГТУ при поддержке РФФИ (грант № 16-01-00184а)
Аннотация
Представлены обоснование и математическая модель задачи принятия оптимальных решений при распределении независимых приоритетов между двумя конкурирующими структурами, взаимодействующими в единой системе. Исследована модель квазилинейного типа с независимыми приоритетами. Приведены условия существования точек глобального максимума целевой функции арбитра и описание этих точек. Рассмотрены специфические ситуации, когда достаточное условие наличия экстремума не выполняется или выполняется только для одного из приоритетов. Приведен пример для случая постоянных приоритетов.
Ключевые слова: квазилинейная модель, оптимизация, глобальный максимум, случайные приоритеты, максимальная эффективность, взаимодействие структур.
Krasiy N.P.
Associate professor, PhD in Physics and Mathematics, Don State Technical University in Rostov-on-Don
OPTIMIZATION OF QUASI-LINEAR MODELS OF SYSTEMS WITH TWO STRUCTURES AND INDEPENDENT PRIORITIES
Abstract
Explanation and mathematical model of the problem of optimal decision making is presented in the case when two independent priorities are distributed among two competing structures interacting in a single system. A model of quasi-linear type with independent priorities is investigated. Conditions of existence and uniqueness of points of global maximum and description of these points are given. Specific situations where sufficient conditions for the existence of extremum are not fulfilled or are fulfilled for only one of the priorities are considered. An example in the case of constant priorities is given.
Keywords: quasi-linear model, optimization, global maximum, random priorities, maximum efficiency, interaction structures.
Подавляющее большинство организаций состоит из нескольких взаимодействующих между собой структур, цели которых зачастую разнонаправлены. Речь идет об организациях разного уровня – от некоторого отдельно взятого предприятия, до целой отрасли, управляемой министерством. Нередко работники управляющих подразделений – арбитры, принимающие решения по обеспечению деятельности такой организации на основании рекомендаций неких экспертов, сталкиваются с проблемой такого распределения приоритетов между ее внутренними структурами, чтобы вся организация имела при этом максимальную эффективность. Возник вопрос о возможности применения математических методов решения этой задачи. В работах [1], [2] представлена математическая формализация задачи, которая показала, что расставляемые приоритеты логично считать случайными величинами, причем решение оптимизационной задачи зависит как от их характера, так и от количества структур, входящих в систему.
Представляемая модель описывает систему с двумя структурами, целевые функции которых «квазилинейного» вида
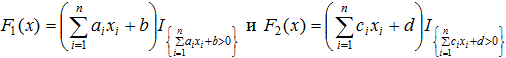
заданы в пространстве Rn, неотрицательны, не обращаются в ноль и дважды непрерывно дифференцируемы на открытых множествах ![]() и
и ![]() соответственно, причём пересечение этих множеств непусто и
соответственно, причём пересечение этих множеств непусто и ![]() .
.
Пусть ![]() — произвольные независимые случайные величины, принимающие значения на некоторых множествах
— произвольные независимые случайные величины, принимающие значения на некоторых множествах ![]() каждая, определенные на некотором вероятностном пространстве
каждая, определенные на некотором вероятностном пространстве ![]() , где
, где ![]() . Естественно предполагать, что
. Естественно предполагать, что
![]() (1)
(1)
Для определения ситуаций, когда существуют точки локальных и глобальных максимумов функции ![]() , найдем ее частные производные:
, найдем ее частные производные:
![]()
возможность дифференцирования под знаком интеграла обосновывается следствием 2.8.7 из [3]). Из того, что ![]() , и из условий (1) вытекает, что
, и из условий (1) вытекает, что ![]() . Таким образом, существование точки
. Таким образом, существование точки ![]() , в которой
, в которой ![]() при всех
при всех ![]() , равносильно выполнению следующих условий:
, равносильно выполнению следующих условий:
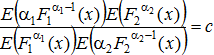 (4)
Для
(4)
Для Начиная с этого момента, будем предполагать, что условие (3) выполнено. Введем в рассмотрение функции:
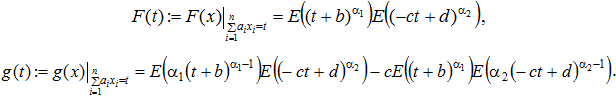
Так как для ![]() выполняются неравенства
выполняются неравенства ![]() , то область определения функций
, то область определения функций ![]() описывается неравенствами
описывается неравенствами ![]() , то есть
, то есть ![]() . Условие непустоты области
. Условие непустоты области ![]() равносильно условию
равносильно условию
![]() (5)
(5)
Итак, доказана следующая
Теорема 1. Для того, чтобы функция ![]() , заданная равенствами (1) и (2), имела стационарные точки, необходимо выполнение условий (3) и (5).
, заданная равенствами (1) и (2), имела стационарные точки, необходимо выполнение условий (3) и (5).
Теорема 2. Пусть выполняются условия (3), (5) и условие
![]() (6)
(6)
Тогда уравнение ![]() имеет единственный корень
имеет единственный корень ![]() и все точки гиперплоскости
и все точки гиперплоскости ![]() являются точками глобального максимума функции
являются точками глобального максимума функции ![]() .
.
Доказательство. Дифференцируя под знаком интеграла (возможность такого дифференцирования опять обосновывается следствием 2.8.7 из [3]), получаем:
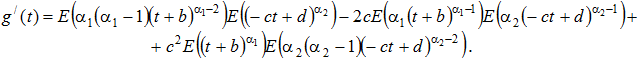
Так как в силу условия ![]() и
и ![]() , а из условия (6) вытекает, что
, а из условия (6) вытекает, что ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() и непрерывная функция
и непрерывная функция ![]() строго монотонно убывает на этом интервале.
строго монотонно убывает на этом интервале.
Покажем теперь, что ![]() . Обозначим
. Обозначим
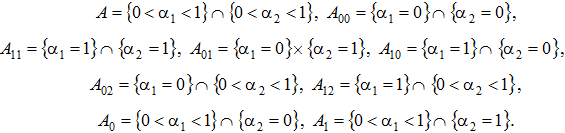 (7)
(7)
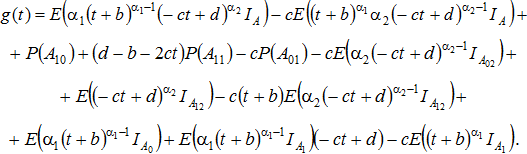 Так как
Так как 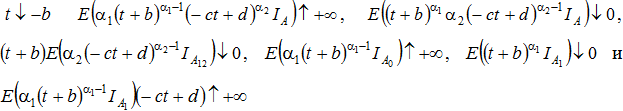 откуда вытекает требуемое утверждение.
Аналогично доказывается, что
откуда вытекает требуемое утверждение.
Аналогично доказывается, что Нами показано, что ![]() — непрерывная строго убывающая на интервале
— непрерывная строго убывающая на интервале ![]() функция, принимающая на нем все действительные значения, а значит, уравнение
функция, принимающая на нем все действительные значения, а значит, уравнение ![]() имеет единственный корень
имеет единственный корень ![]() . Кроме того ясно, что
. Кроме того ясно, что ![]() — единственная точка локального максимума функции
— единственная точка локального максимума функции ![]() , а, значит, и единственная точка глобального максимума на
, а, значит, и единственная точка глобального максимума на ![]() . Следовательно, все точки гиперплоскости
. Следовательно, все точки гиперплоскости ![]() являются точками глобального максимума функции
являются точками глобального максимума функции ![]() . Теорема доказана [4].
. Теорема доказана [4].
Замечание 1. Пусть выполняются условия (3), (5), а условие (6) не выполняется. Учитывая (1) и обозначения (7), имеем:
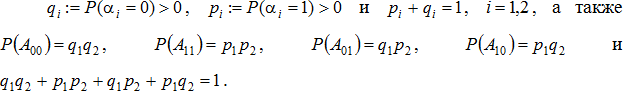
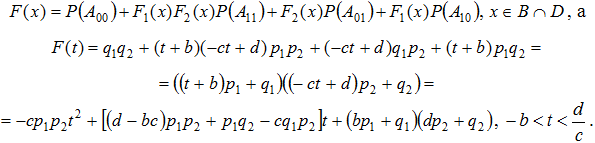
Таким образом, график функции ![]() – парабола с ветвями, направленными вниз, имеющая 2 точки пересечения с осью абсцисс (очевидно, что
– парабола с ветвями, направленными вниз, имеющая 2 точки пересечения с осью абсцисс (очевидно, что  ), а её точкой глобального максимума является вершина параболы с абсциссой
), а её точкой глобального максимума является вершина параболы с абсциссой
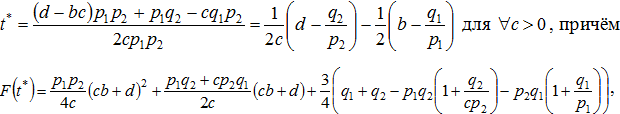
а все точки гиперплоскости ![]() являются точками глобального максимума функции
являются точками глобального максимума функции ![]() [5].
[5].
Замечание 2. Пусть выполняются условия (3), (5), а условие (6) выполнено только для одного из приоритетов, например, для α2. То есть, учитывая обозначения (7),
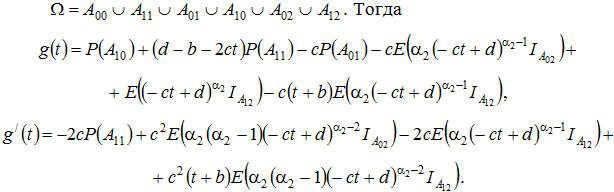
Так как из условия (6) для α2 следует, что ![]() , то очевидно, что
, то очевидно, что ![]() (аналогично доказательству теоремы 2).
(аналогично доказательству теоремы 2).
Так же, опираясь на доказательство теоремы 2, нетрудно показать, что
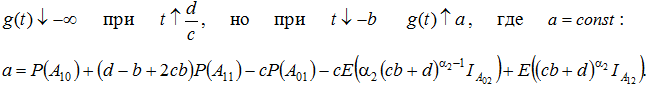
И если ![]() , то, как и в теореме 2, в результате имеем единственный корень
, то, как и в теореме 2, в результате имеем единственный корень ![]() с такими же выводами, а если
с такими же выводами, а если ![]() , то корней уравнения
, то корней уравнения ![]() нет и нет точек глобального максимума функции
нет и нет точек глобального максимума функции ![]() .
.
Покажем, что число a может иметь разные знаки. Пусть ![]() , тогда, используя обозначения замечания 1,
, тогда, используя обозначения замечания 1,
![]()
Чтобы ![]() , нужно чтобы знаки числителя и знаменателя дроби совпадали. Если
, нужно чтобы знаки числителя и знаменателя дроби совпадали. Если ![]() , то таким условием является неравенство
, то таким условием является неравенство 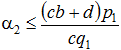 . Например, при
. Например, при ![]() . То есть, при
. То есть, при ![]()
Если ![]() , то числитель не может быть положителен, так как неравенство
, то числитель не может быть положителен, так как неравенство 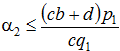 невыполнимо. Значит, наличие решения зависит от отрицательности знаменателя. Так как
невыполнимо. Значит, наличие решения зависит от отрицательности знаменателя. Так как ![]() , предположим, что
, предположим, что ![]() . Знаменатель отрицателен при выполнении условий: n нечётное, n-m нечётное. Например, при
. Знаменатель отрицателен при выполнении условий: n нечётное, n-m нечётное. Например, при ![]() для
для ![]() условия выполнены,
условия выполнены, ![]() и единственное решение существует, а при
и единственное решение существует, а при ![]() и решения нет [5].
и решения нет [5].
Пример. Пусть ![]() . Тогда уравнение (4) принимает вид:
. Тогда уравнение (4) принимает вид:
Единственным корнем этого уравнения является ![]() , а глобальным максимумом –
, а глобальным максимумом – 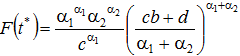 .
.
В случае, когда ![]() , результат соответствует примеру 1, представленному в работе [2]:
, результат соответствует примеру 1, представленному в работе [2]: ![]() с соответствующими выводами.
с соответствующими выводами.
Список литературы / References
- Вагин, В.С. Оптимизация квазилинейных моделей сложных систем с учетом вероятностного характера приоритетов. / В.С. Вагин, И.В. Павлов // Международная конференция “XXVI Крымская осенняя математическая школа-симпозиум по спектральным и эволюционным задачам”. – Сборник тезисов. – 2015. – С. 109.
- Вагин В.С., Павлов И.В. Моделирование и оптимизация квазилинейных сложных систем с учетом вероятностного характера приоритетов. // Вестник РГУПС, 2016, №1(61), С. 135–139.
- Богачев, В.И. Основы теории меры. / В.И. Богачев. – Москва-Ижевск: НИЦ Регулярная и хаотическая динамика, 2006. – Т. 1. – С. 584.
- Красий Н.П. Оптимизация квазилинейных моделей с независимыми приоритетами. // Современные методы и проблемы теории операторов и гармонического анализа и их приложения – VI, Ростов-на-Дону, 24-29 апреля 2016 г., материалы конференции, С. 134-135.
- Красий Н.П. О некоторых особых случаях оптимизации квазилинейных моделей с независимыми приоритетами // Международная конференция “XXVII Крымская осенняя математическая школа-симпозиум по спектральным и эволюционным задачам”. – Сборник тезисов. – 2016. – С. 110.
Список литературы на английском языке / References in English
- Vagin, V.S. Optimizatsiya kvazilineynyh modeley slozhnyh system s uchetom veroyatnostnogo haraktera prioritetov. [Optimization of quasi-linear models of complete systems in view of random nature of priorities.] / V.S. Vagin, I.V. Pavlov // Mezhdunarodnay konferentsiya “ XXVI Krymskaya osennyaya matenatitcheskaya shkola-simpozium po spektralnim i evoluzionnim zadatcham” [International Conference “KROMSH-XXVI”. Abstracts.] – 2015. – P. 109. [in Russian]
- S. Vagin, I.V. Pavlov. Modelirovanie i optimizatsiya kvazilineynih slozhnyh system s uchetom veroyatnostnogo haraktera prioritetov. [Modeling and Optimization of quasi-linear complete systems in view of random nature of priorities.]// Vestnik RGUPS [Vestnik RGUPS], 2016, №1(61), Р. 135–139. [in Russian]
- Bogachev, V.I. Osnovy teorii mery. [Foundations of Measure Theory.] / V.I. Bogachev. – Moskva-Ijevsk: NITs Regulyarnaya i haotitcheskaya dinamika [Moscow-Izhevsk: Scientific and Publishing Center Regular and chaotic dynamics], 2006. – V. 1. – P. 584. [in Russian]
- Krasiy N.P. Optimizatsiya kvazilineynyh modelej s nezavisimimi prioritetami. [Optimization of quasi-linear models with independent priorities] // Sovremennye metody i problemi teorii operatorov i garmonicheskogo analiza i ih prilozheniya [Modern methods and problems of operator theory and harmonic analysis and their applications] – VI, Rostov-on-Don, 24-29 April 2016, P. 134-135. [in Russian]
- Krasiy N.P. O nekotoryh osobyh slutchayah optimizatsiyi kvazilineynyh modelej s nezavisimimi prioritetami. [On some special cases of the optimization of quasi-linear models with independent priorities] // Mejdunarodnay konferentsiya “ XXVI Krymskaya osennyaya matenatitcheskaya shkola-simpozium po spektralnym i evoluzionnym zadatcham” [International Conference “KROMSH-XXVI”. Abstracts.] – 2016. – P. 110. [in Russian]
