ESTIMATES FOR THE SOLUTION IN С0(S12) METRIC OF A QUASILINEAR EQUATION OF GENERAL FORM
ОЦЕНКИ РЕШЕНИЯ В МЕТРИКЕ С0(S12) НЕКОТОРОГО КВАЗИЛИНЕЙНОГО УРАВНЕНИЯ ОБЩЕГО ВИДА
Научная статья
Юрьева Т.А.1, *, Чалкина Н.А.2
1 ORCID: 0000-0002-8434-4817;
1, 2 Амурский государственный университет; Благовещенск, Россия
* Корреспондирующий автор (yuryevatat[at]mail.ru)
АннотацияВопросы существования и единственности регулярных поверхностей с заданными геометрическими характеристиками в том или ином пространстве в аналитическом плане эквивалентны рассмотрению и исследованию на однозначную разрешимость дифференциальных уравнений в частных производных на том или ином многообразии. В статье приводится доказательство существование априорных оценок решения квазилинейного уравнения общего вида на единичной сфере S12, а также рассматриваются частные случаи обобщенного квазилинейного уравнения, связанные с геометрическими задачами.
Ключевые слова: квазилинейное уравнение, положительная эллиптичность, априорные оценки, квадратичная форма.
ESTIMATES FOR THE SOLUTION IN С0(S12) METRIC OF A QUASILINEAR EQUATION OF GENERAL FORM
Research article
Yurieva T.A.1, *, Chalkina N.A.2
1 ORCID: 0000-0002-8434-4817
1, 2 Amur State University; Blagoveshchensk, Russia
* Corresponding author (yuryevatat[at]mail.ru)
AbstractThe questions of the existence and uniqueness of regular surfaces with the given geometric characteristics in one or another space are analytically equivalent to considering and investigating the unique solvability of partial differential equations on one or another manifold. The paper provides a proof that a priori estimates for the solution of a generalized quasilinear equation on the unit sphere S12 exist. It also considers special cases of a generalized quasilinear equation related to geometric problems.
Keywords: quasilinear equation, positive ellipticity, a priori estimates, quadratic form.
ВведениеГеометрическая задача о восстановлении регулярной поверхности в различных пространствах [1], [2], [3] по заданным геометрическим характеристикам связана с исследованием однозначной разрешимости дифференциальных уравнений в частных производных на том или ином многообразии.
Например, если в трехмерном евклидовом пространстве E3 имеем регулярную гомеоморфную сфере S12 (радиус сферы равен единице, O – некоторая фиксированная точка пространства E3) поверхность, заданную в локальных сферических координатах явно функцией ρ=ρ(u, v) ((u, v)ϵS12, ρϵR+) и, кроме того, есть функция H(u, v, ρ)ϵS12× R+, обладающая тем свойством, что средняя кривизна указанной выше поверхности в каждой точке совпадает со значением функции H(u, v, ρ) в той же точке, то задача существования и единственности такой поверхности равносильна исследованию на однозначную разрешимость следующего квазилинейного уравнения на двумерном многообразии, каковым является сфера S12:
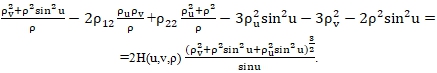
Здесь конечный атлас на S12 выбран с условием, что локальные географические координаты этого атласа удовлетворяют неравенству: sinu≥x>0, а ρ11=ρuu, ρ12=ρuv ![]() ρv, ρ22=ρvv+sinucosuρu есть ковариантные производные второго порядка относительно метрики единичной сферы S12.
ρv, ρ22=ρvv+sinucosuρu есть ковариантные производные второго порядка относительно метрики единичной сферы S12.
В рассматриваемой геометрической задаче выпуклость поверхности не предполагается [1].
Первым этапом в исследовании дифференциального уравнения, связанного с обозначенной геометрической задачей, является получение априорных оценок в различных метриках [4], [5], [7].
Основное содержание работы
В работе [6] мы ввели более общее квазилинейное уравнение на единичной сфере S12, которое не связано ни с какой геометрической задачей. Это уравнение имеет вид:
f(ρ)d(u,v)(ρ11ρv2–2ρ12ρuρv+ρ22ρu2)+φ(ρ)(ρ11φ1(u,v)+ ρ22φ2(u,v))+D(u,v,ρ,ρu,ρv)=ψ(u,v,ρ)∙D1(u,v,ρ,ρu,ρv),где (u, v)ϵS12, ρϵR+, ρ=ρ(u, v) – решение уравнения; ρ11, ρ12, ρ22 – вторые ковариантные производные регулярной функции ρ(u, v) относительно метрики S12.
На функции, входящие в данное уравнение наложены следующие условия: f(ρ)>0, d(u,v)>0, φ(ρ)>0, φ1(u,v)>0, φ2(u,v)>0, D1(u,v,ρ,ρu,ρv) при ρu=ρv=0, то есть D1(u,v,ρ,0,0) положительно.
Приведенное выше уравнение является положительно эллиптичным квазилинейным уравнением на своем решении ρ(u, v).
Действительно, пусть Ф(u,v,ρ,ρu,ρv,ρ11,ρ12,ρ22)=0 есть краткая запись уравнения.
Квадратичная форма ![]() (ξ,ηϵR) для приведенного уравнения общего вида следующая: A∙ξ2–2B∙ξ∙η+C∙η2, где A=f(ρ)d(u,v)ρv2+φ(ρ)φ1(u,v), B=f(ρ)d(u,v)ρuρv, C=f(ρ)d(u,v)ρu2+φ(ρ)φ2(u,v). Эта форма положительно определена, так как ее дискриминант AC–B2=f(ρ)d(u,v)ρv2∙φ(ρ)φ2(u,v)+φ(ρ)φ1(u,v)∙f(ρ)d(u,v)ρu2 положителен в силу наложенных на функции f(ρ), d(u,v), φ(ρ), φ1(u,v), φ2(u,v) условий, а коэффициент A>0 вследствие тех же причин.
(ξ,ηϵR) для приведенного уравнения общего вида следующая: A∙ξ2–2B∙ξ∙η+C∙η2, где A=f(ρ)d(u,v)ρv2+φ(ρ)φ1(u,v), B=f(ρ)d(u,v)ρuρv, C=f(ρ)d(u,v)ρu2+φ(ρ)φ2(u,v). Эта форма положительно определена, так как ее дискриминант AC–B2=f(ρ)d(u,v)ρv2∙φ(ρ)φ2(u,v)+φ(ρ)φ1(u,v)∙f(ρ)d(u,v)ρu2 положителен в силу наложенных на функции f(ρ), d(u,v), φ(ρ), φ1(u,v), φ2(u,v) условий, а коэффициент A>0 вследствие тех же причин.
Итак, уравнение, исследуемое нами, является положительно эллиптичным квазилинейным уравнением на сфере S12 как двумерном многообразии.
Сформулируем основное положение данной работы.
Обозначим через ![]() , D1(u,v,ρ,ρu,ρv)>0.
, D1(u,v,ρ,ρu,ρv)>0.
Если функция ψ(u, v, ρ) принадлежит S12× R+ и удовлетворяет следующим условиям:
1) ψ(u, v, ρ)>H0 при ρ<ρ1;
2) ψ(u, v, ρ)<H0 при ρ>ρ2, то имеет место априорная оценка решения ρ=ρ(u, v): ρ1≤ρ(u, v)≤ρ2.(ρ1<ρ2), ρ1ϵR+, ρ2ϵR+). Это неравенство означает наличие априорной оценки решения исследуемого уравнения в метрике C0(S12).
Проверим справедливость этого утверждения.
Пусть (u0, v0)ϵS12 – точка минимума функции ρ=ρ(u, v) – решения исходного уравнения.
Эта точка существует, так как ρ=ρ(u, v) – регулярная функция, а сфера S12 – компактное многообразие.
В точке (u0, v0) будем иметь: ρ11=ρuu, ρ12=ρuv, ρ22=ρvv, ρu=ρv=0, d2ρ≥0, ![]() D1(u,v,ρ,0,0)>0.
D1(u,v,ρ,0,0)>0.
Исследуемое уравнение положительно эллиптично, то есть квадратичная форма T(Ф,ρ)≥0.
Из свойств квадратичных форм следует, что неравенства d2ρ≥0 и T(Ф,ρ)≥0 дают следующее:
ρ11(f(ρ)d(u,v)ρv2+φ(ρ)φ1(u,v))–2ρ12f(ρ)d(u,v)ρuρv+ρ22(f(ρ)d(u,v)ρu2+ +φ(ρ)φ2(u,v))≥0, или f(ρ)d(u,v)(ρ11ρv2–2ρ12ρuρv+ρ22ρu2)+φ(ρ)(ρ11φ1(u,v)+ ρ22φ2(u,v))≥0. Напомним, что в точке (u0, v0) будем иметь: ρ11=ρuu, ρ12=ρuv, ρ22=ρvv.Так как левая часть полученного неравенства есть часть исследуемого уравнения, то отсюда следует неравенство:
ψ(u,v,ρ)∙D1(u,v,ρ,0,0)–D(u,v,ρ,0,0)≥0, ψ(u,v,ρ)≥ ![]()
Таким образом, ψ(u, v, ρ)≥H0 в точке минимума (u0, v0) решения уравнения ρ=ρ(u, v).
Предположим теперь, что ρ(u0, v0)<ρ1. Тогда из условия сформулированного основного предложения функция ψ(u, v, ρ)<H0, что противоречит полученному нами неравенству. Следовательно, ρ(u0, v0)>ρ1. Отсюда следует оценка снизу на решение уравнения ρ=ρ(u, v): ρ1≤ ρ(u0, v0)≤ρ(u, v), ρ1≤ ρ(u, v).
Допустим теперь, что (u1, v1)ϵS12 есть точка максимума функции ρ(u, v), которая является решением исходного уравнения. Эта точка существует в силу тех же причин, что дают существование точки минимума ρ(u, v), то есть точки (u0, v0).
В точке максимума функции ρ(u, v) второй дифференциал d2ρ ≤0, первые производные ρu=ρv=0, а вторые ковариантные производные ρ(u, v) относительно метрики S12 совпадают с обычными производными: ρ11=ρuu, ρ12=ρuv, ρ22=ρvv. Выражение ![]() в точке (u1, v1) равно
в точке (u1, v1) равно ![]() D1(u,v,ρ,0,0)>0.
D1(u,v,ρ,0,0)>0.
В силу положительной эллиптичности исследуемого уравнения квадратичная форма T(Ф,ρ) положительно определена.
Из перечисленных фактов, свойств квадратичных форм T(Ф,ρ) и d2ρ из исходного уравнения следует:
ρ11(f(ρ)d(u,v)ρv2+φ(ρ)φ1(u,v))–2ρ12f(ρ)d(u,v)ρuρv+ρ22(f(ρ)d(u,v)ρu2+φ(ρ)φ2(u,v))=f(ρ)d(u,v)(ρ11ρv2–2ρ12ρuρv+ρ22ρu2)+φ(ρ)(ρ11φ1(u,v)+ ρ22φ2(u,v))≤0, то есть ψ(u, v, ρ)∙D1(u,v,ρ,ρu,ρv)–D(u,v,ρ,ρu,ρv)≤0 в точке (u1, v1).
Отсюда следует неравенство: ψ(u, v, ρ)≤ ![]() D1(u,v,ρ,0,0)>0, или ψ(u, v, ρ)≤H0 в точке максимума функции ρ(u, v) – решения исходного уравнения.
D1(u,v,ρ,0,0)>0, или ψ(u, v, ρ)≤H0 в точке максимума функции ρ(u, v) – решения исходного уравнения.
Предположим теперь, что ρ(u, v)>ρ2. По условию сформулированного основного предложения ψ(u, v, ρ)>ψ0, что противоречит полученному неравенству. Это означает, что ρ(u1, v1)≤ρ2. Тогда имеем априорную оценку решения исходного уравнения сверху: ρ(u, v)≤ρ(u1, v1)≤ρ2, или ρ(u, v)≤ρ2.
Таким образом, мы получили априорные оценки решения ρ(u, v) исследуемого уравнения в метрике C0(S12): ρ1≤ρ(u, v)≤ρ2.
Утверждение, сформулированное в работе, доказано.
Частные случаи общего квазилинейного уравнения, связанного с геометрическими задачами.
- В начале статьи мы ввели квазилинейное уравнение, которое является аналитической интерпретацией геометрической задачи о восстановлении регулярной гомеоморфной сфере S12 поверхности в трехмерном евклидовом пространстве E3.
В этом положительно эллиптичном уравнении f(ρ)= ![]() , d(u,v)=1>0, φ(ρ)=ρ>0, φ1(u,v)=sin2u>0, φ2(u,v)=1>0, D=–
, d(u,v)=1>0, φ(ρ)=ρ>0, φ1(u,v)=sin2u>0, φ2(u,v)=1>0, D=– ![]()
- Частным случаем нашего общего положительно эллиптичного уравнения является следующее уравнение:
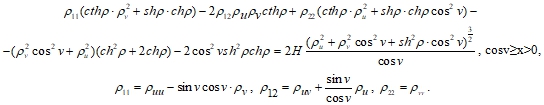
Это уравнение мы приводим в работе [6]. Оно является аналитической моделью геометрической задачи о восстановлении регулярной гомеоморфной сфере поверхности с заданной функцией средней кривизны в гиперболическом пространстве H3.
Здесь f(ρ)=cthρ>0, d(u,v)=1>0, φ(ρ)=shρchρ>0, D1(u,v,ρ,ρu,ρv)= ![]() , D1(u,v,ρ,0,0)=sh3ρ∙cos2v>0.
, D1(u,v,ρ,0,0)=sh3ρ∙cos2v>0.
Заключение
Научная новизна проведенной работы заключается в доказательстве существования априорных оценок решения введенного квазилинейного уравнения общего вида, не связанного с геометрическими задачами, на единичной сфере S12. Следующим этапом исследования планируется построение однопараметрического семейства квазилинейных уравнений общего вида на сфере.
| Благодарности Выражаем благодарность за помощь в проведении исследования Филимоновой Анне Павловне. | Acknowledgement We are grateful for the assistance in conducting the study to Anna Filimonova. |
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Бакельман И.Я. Существование гомеоморфной сфере поверхности в евклидовом пространстве с заданной средней кривизной /И.Я. Бакельман, Б.Е. Кантор // Геометрия и топология: Сб. научн. трудов. – ЛГПИ им. А.И. Герцена. – Л., 1974. – вып. 1. – С. 3-10
- Верещагин Б.М. Восстановление замкнутой выпуклой поверхности по данной функции гауссовой кривизны /Б.М. Верещагин // Вопросы глобальной геометрии: Сб. научн. трудов. – ЛГПИ им. Л. И. Герцена. – Л., 1979. – С. 7-12.
- Кантор Б.Е. О единственности гомеоморфной сфере гиперповерхности с данной функцией средней кривизны в евклидовом пространстве / Б.Е. Кантор // Геометрия: Сб. научн. трудов. – ЛГПИ им. А.И. Герцена. – Л., 1975. – С. 59-61.
- Филимонова А.П. Оценка в метрике и единственность выпуклой гомеоморфной сфере поверхности с заданной гауссовой кривизной в / А.П. Филимонова // Вопросы глобальной геометрии: Сб. научн. трудов. – ЛГПИ им. А.И. Герцена. – Л., 1979. – С. 64-68.
- Филимонова А.П. Единственность решения уравнения Монжа – Ампера некоторого класса на сфере как двумерном многообразии /А.П. Филимонова, Т.А. Юрьева // Международный научно-исследовательский журнал. – № 6-5 (48). – 2016. – С. 107-110.
- Филимонова А.П. Линеаризация как метод доказательства единственности решения для некоторого класса нелинейных дифференциальных уравнений на сфере /А.П. Филимонова, Т.А. Юрьева // Вестник Амурского государственного университета. Серия: Естественные и экономические науки. – 2016. – № 73. – С. 25-28.
- Филимонова А.П. Априорные оценки градиента решения уравнения некоторого класса Монжа – Ампера /А.П. Филимонова, Т.А. Юрьева // Вестник Бурятского государственного университета. Математика, информатика. – 2019. – № 1. – С. 49-55.
Список литературы на английском языке / References in English
- Bakel'man I.Ja. Sushhestvovanie gomeomorfnoj sfere poverhnosti v evklidovom prostranstve s zadannoj srednej kriviznoj [The existence of a homeomorphic sphere of a surface in Euclidean space with a given average curvature] /I.Ja. Bakel'man, B.E. Kantor // Geometrija i topologija: Sb. nauchn. trudov [Geometry and Topology: Sat. scientific labor]. – LGPI im. A.I. Gercena. – L., 1974. – issue 1. – P. 3-10. [in Russian]
- Vereshhagin B.M. Vosstanovlenie zamknutoj vypukloj poverhnosti po dannoj funkcii gaussovoj krivizny [Reconstruction of a closed convex surface from a given function of Gaussian curvature] /B.M. Vereshhagin // Voprosy glo-bal'noj geometrii: Sb. nauchn. trudov [Questions of global geometry: Sat. scientific labor.]. – LGPI im. L. I. Gercena. – L., 1979. – P. 7-12. [in Russian]
- Kantor B.E. O edinstvennosti gomeomorfnoj sfere giperpoverhnosti s dannoj funkciej srednej krivizny v evklidovom prostranstve [On the uniqueness of a homeomorphic hypersurface sphere with a given function of average curvature in Euclidean space] / B.E. Kantor // Geometrija: Sb. nauchn. trudov [Geometry: Sat. scientific labor.]. – LGPI im. A.I. Gercena. – L., 1975. – P. 59-61. [in Russian]
- Filimonova A.P. Ocenka v metrike i edinstvennost' vypukloj gomeomorfnoj sfere poverhnosti s zadannoj gaussovoj kriviznoj v [Estimation in the metric and uniqueness of a convex homeomorphic sphere of a surface with a given Gaussian curvature in ] / A.P. Filimonova // Voprosy global'noj geometrii: Sb. nauchn. trudov [Questions of global geometry: Sat. scientific labor.]. – LGPI im. A.I. Gercena. – L., 1979. – P. 64-68. [in Russian]
- Filimonova A.P. Edinstvennost' reshenija uravnenija Monzha – Ampera nekotorogo klassa na sfere kak dvumernom mnogoobrazii [Uniqueness of the solution of the Monge - Ampère equation of a certain class on a sphere as a two-dimensional manifold] /A.P. Filimonova, T.A. Jur'eva // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Research Journal]. – № 6-5 (48). – 2016. – P. 107-110. [in Russian]
- Filimonova A.P. Linearizacija kak metod dokazatel'stva edin-stvennosti reshenija dlja nekotorogo klassa nelinejnyh differenci-al'nyh uravnenij na sfere [Linearization as a method of proving the uniqueness of a solution for a class of nonlinear differential equations on the sphere] /A.P. Filimonova, T.A. Jur'eva // Vestnik Amurskogo gosudarstvennogo universiteta. Serija: Estestvennye i jekonomicheskie nauki [Bulletin of the Amur State University. Series: Natural and Economic Sciences]. – 2016. – № 73. – P. 25-28. [in Russian]
- Filimonova A.P. Apriornye ocenki gradienta reshenija uravne-nija nekotorogo klassa Monzha – Ampera [Priori estimates of the gradient of the solution of an equation of a certain Monge – Ampère class] /A.P. Filimonova, T.A. Jur'eva // Vestnik Burjatskogo gosudarstvennogo universiteta. Matematika, informatika [Bulletin of the Buryat State University. Mathematics, computer science]. – 2019. – № 1. – P. 49-55. [in Russian]
