Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

О ВОЛНОВОЙ ФУНКЦИИ ФОТОНА В КООРДИНАТНОМ И ИМПУЛЬСНОМ ПРЕДСТАВЛЕНИЯХ

Научная статья
Давыдов А. П.
Злыднева Т. П.
DOI:
https://doi.org/10.18454/IRJ.2016.53.104
Выпуск: № 11 (53), 2016
Опубликована:
2016/11/18
PDF

Давыдов А. П.1, Злыднева Т. П.2

1Кандидат физико-математических наук, доцент, 2Кандидат педагогических наук, доцент, Магнитогорский государственный технический университет им. Г.И. Носова

О ВОЛНОВОЙ ФУНКЦИИ ФОТОНА В КООРДИНАТНОМ И ИМПУЛЬСНОМ ПРЕДСТАВЛЕНИЯХ 

Аннотация

В статье приводится явный вид волновой функции свободного фотона в координатном и импульсном представлениях. Обсуждается отличие сконструированной волновой функции фотона в импульсном представлении от используемых вариантов в литературе. Указывается, что понятие волнового цуга, отнесенное к волновой функции фотона в координатном представлении, является более корректным при описании интерференции, чем аналогичное понятие классической электродинамики. Это позволяет значительно смягчить проблему корпускулярно-волнового дуализма света.

Ключевые слова: волновой пакет, бивектор, уравнение  Шредингера.

Davydov A. P.1, Zlydneva T. P.2

1PhD in Physics and Mathematics, Associate professor, 2PhD in Pedagogy, Associate professor,  Nosov Magnitogorsk State Technical University

ON THE RELATIVISTIC INVARIANCE OF THE CONTINUITY EQUATION IN QUANTUM MECHANICS OF THE PHOTON

Abstract

The article provides an explicit form of the wave function of a free photon in the coordinate and momentum representations. The difference of the constructed photon wave function in the momentum representation, from its variants that used in the literature, is discussed. It is stated that the concept of the wave train, referred to the photon coordinate wave function, is more correct in describing interference than the analogous concept of classical electrodynamics. This allows to considerably mitigate the problem of wave-particle duality of light.

Keywords: wave packet, bivector, Schrödinger equation.

Построение волновой функции фотона в координатном представлении долгие десятилетия считалось невозможным, по-видимому, начиная с работы [1]. Однако в настоящее время ее актуальность начинает вновь рассматриваться в связи с новыми оптические явлениями, в которых участвуют одно- и двухфотонные состояния (квантовая запутанность, квантовые компьютеры, передача информации по квантовым каналам связи и др.). В [2–8] предлагалась волновая функция фотона, нормированная на единичную вероятность, сконструированная на основе уравнений Максвелла, записанных в форме Майорана для векторов  19-01-2017 10-00-52, где E и H – напряженности поля. В соответствии с [5–8], она имеет вид

19-01-2017 10-02-30  (1)

где 19-01-2017 10-03-11  (2)

(Oe) – единица измерения (эрстед) векторов ξ, η. Их можно использовать для конструирования бивектора 19-01-2017 10-05-20 с целью описания состояния фотона [9]. Однако в [9] этот бивектор, не нормируемый на единичную вероятность, упоминался лишь формально и, по сути, не был использован, хотя бы даже для квантования электромагнитного поля. Кроме того, в [9] подчеркивалось, что из данного бивектора нельзя построить плотность вероятности нахождения фотона в данной точке конфигурационного пространства.

Тем не менее, бивектор подобного вида может играть важную вспомогательную роль с целью построения волновой функции фотона (1), нормированной на единичную вероятность. В [5–8] построен бивектор

19-01-2017 10-07-41  (3)

где верхние знаки индексов отвечают положительной энергии фотона, а нижние – отрицательной, «теоретически возможной», с точки зрения виртуальных состояний. Числа 19-01-2017 10-09-02 в (3) являются значениями спиральности λ. В [5–8] утверждается, что коэффициенты разложения 19-01-2017 10-10-49 однозначно выражаются через векторы E и H, если с их помощью задать состояние фотона в терминах классического электромагнитного поля. Также, в [5–8] установлено, что базисные бивекторы 19-01-2017 10-11-24 описывают состояния фотона с определенными значениями его импульса 19-01-2017 10-11-58, энергии 19-01-2017 10-12-33  и спиральности λ. Эти базисные векторы имеют следующий вид:

19-01-2017 10-14-53  (4)

19-01-2017 10-15-33  (5)

где 19-01-2017 10-17-01 – комплексные векторы поляризации [5–8]: 19-01-2017 10-17-35  (6)

19-01-2017 10-18-37  – вещественные взаимно перпендикулярные векторы, образующие правую тройку с вектором n=k/k  (при заданном  волновом векторе k=p/ħ):

19-01-2017 10-40-17  (7)

Формулы (7) реализуют ортонормированность векторов 19-01-2017 10-41-23 и некоторые важные соотношения, если 19-01-2017 10-42-07 не меняется при изменении знака вектора n:

19-01-2017 10-43-03  (8)

В свою очередь, соотношения (8) обеспечивают ортонормированность бивекторов (4), (5), обусловливающую возможность разложения (3):

19-01-2017 10-43-56   (9)

С помощью бивектора (3) пространственная плотность распределения энергии фотона в состоянии, описываемом этим бивектором или соответствующей волновой функцией 19-01-2017 10-44-43  вида (1), записывается как

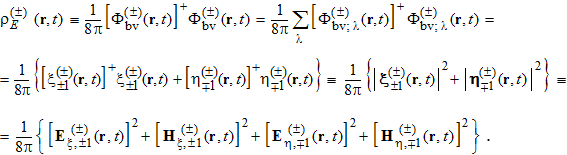19-01-2017 10-45-46  (10)

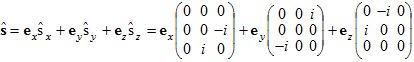При этом волновая функция (1) удовлетворяет уравнению вида Шредингера: 19-01-2017 10-46-30   (11) так же, как и бивектор 19-01-2017 10-47-17, определяемый в (3), где оператор Гамильтона 19-01-2017 10-47-54  (12) матрица 19-01-2017 10-48-37,  – оператор спина фотона в векторном представлении: 19-01-2017 10-49-07  (13)

Описание состояния фотона с помощью волновой функции (1), нормированной на единичную вероятность, удовлетворяющей уравнению (11) и уравнению непрерывности [5–8] (см. ниже (15)) означает, очевидно, «первичное квантование» состояний фотона.

В [7–8, 10, 11] функция (1) применялась для однофотонного моделирования лазерного излучения в фемтосекундном диапазоне, с коэффициентами 19-01-2017 10-50-26, параметризированными в гауссовой форме

19-01-2017 10-51-01  (14)

Волновую функцию (1) можно применить для объяснения интерференции света [12]. Как известно, в классической электродинамике интерференция света имеет место для (более-менее) монохроматических волн. Волновой пакет (1) в пределе 19-01-2017 10-52-17 в (14) трансформируется в плоскую монохроматическую волну, с сохранением нормировки на единичную вероятность. Именно такого вида волновой пакет, описывающий однофотонное состояние, при объяснении интерференции света приходит на замену некоего цуга («обрывка синусоиды») «реального» излучения (длительностью τ) электромагнитной волны одним атомом, привлекаемой в классической электродинамике. При этом, согласно соотношению неопределенностей для энергии и времени, при увеличении степени монохроматичности (когда неопределенность энергии фотона стремится к нулю) увеличивается время τ, в течение которого фотон должен быть излучен. Длительность же самого процесса излучения, однако, весьма мала, возможно, гораздо меньше, чем длительность, которая полагается в классической электродинамике, совпадающая со временем существования возбужденного состояния атома (порядка 19-01-2017 10-54-04 для не метастабильных состояний).  Время τ, тем не менее, играет такую же роль, что и время когерентности в классической электродинамике. Можно также говорить и о «длине цуга» 19-01-2017 10-55-37 для одиночного фотона, причем с большей корректностью, чем о нем говорят в классической электродинамике, так как «разделение» неизмеряемой волновой функции (1) на несколько частей, идущих потом по разным оптическим путям, ничем не запрещено [13].

Волновая функция (1) удовлетворяет уравнению непрерывности [5–8],

19-01-2017 10-56-49   (15)

где

19-01-2017 10-57-35  (16)

Волновой функции (1) соответствует волновая функция в импульсном представлении, согласно общим положениям квантовой механики:

19-01-2017 10-58-29   (17)

Если 19-01-2017 10-59-16 известны, то, используя функции (1) или (17), можно вычислить все характеристики состояния фотона, например, его среднюю энергию

19-01-2017 10-59-58   (18)

Эта формула дает значение, совпадающее с имеющимся в классической электродинамике [5–8]. Данное обстоятельство выражает принцип соответствия, обусловливающий введение волновой функции (1). Вместе с тем, в традиционных изложениях вторичного квантования электромагнитного поля встречаются выражения, аналогичные (18), исходя из которых делается неправильный вывод, что совокупность коэффициентов 19-01-2017 10-59-16 является волновой функцией фотона в импульсном представлении (при этом 19-01-2017 10-59-16 не подразумеваются удовлетворяющими разложению (1)). Отсюда проистекает некорректная аргументация, что хотя в импульсном представлении волновая функция фотона существует, в координатном – она отсутствует [9]. Например, типичное выражение для энергии электромагнитного поля, сопоставляемой энергии одного фотона, имеет вид

19-01-2017 11-03-01  (19)

Если на функцию 19-01-2017 11-03-41 наложить условие нормировки 19-01-2017 11-04-13   (20)

то из (19), (20) следует, что 19-01-2017 11-05-07 можно отождествить с плотностью импульсного распределения. В связи с этим, сама функция 19-01-2017 11-05-41, часто полагается волновой функцией фотона в импульсном представлении (см., например, [9], с. 84). На наш взгляд, “правильной” волновой функцией фотона является бивектор (3) или волновой пакет (1). Поэтому в импульсном представлении волновой функцией фотона [см. (17)] является компонента Фурье от волновой функции в координатном представлении (1).

Введение волновой функции фотона позволяет смягчить проблему корпускулярно-волнового дуализма [6–8]. В [14] обсуждается построение волновой функции фотона в терминах комплексных потенциалов, возникающих при «извлечении квадратного корня» из волнового уравнения.

Список литературы / References

  1. Landau L. Quantenelectrodynamik im Konfigurationsraum / L. Landau, R. Peierls // Zeit. F. Phys. – 1930. – V. 62. – P. 188–198.
  2. Bialynicki-Birula I. On the wave function of the photon / I. Bialynicki-Birula // Acta Phys. Pol. A. – 1994. – V. 86. – P. 97–116.
  3. Sipe J. Photon wave functions // Phys. Rev. A. – 1995. – V. 52. – P. 1875.
  4. Давыдов А. П. Квантовая механика фотона / А. П. Давыдов // НАУКА И ШКОЛА: тез. докл. XXXIII науч. конф. МГПИ. – Магнитогорск: Изд-во МГПИ, 1995. – С. 206–207.
  5. Давыдов А. П. Волновая функция фотона в координатном представлении / А. П. Давыдов // Вестник МаГУ: Периодический научный журнал. Вып. 5. Естественные науки. – Магнитогорск: Изд-во МаГУ, 2004. – С. 235–243.
  6. Давыдов А. П. Квантовая механика фотона: волновая функция в координатном представлении / А. П. Давыдов // Электромагнитные волны и электронные системы. – 2015. – Т. 20. – № 5. – С. 43–61.
  7. Давыдов А. П. Волновая функция фотона в координатном представлении. – Магнитогорск: МГТУ им. Г.И. Носова, 2015. – 180 с.
  8. Давыдов А. П. Однофотонный подход к моделированию короткоимпульсного лазерного излучения [Электронный ресурс] / А. П. Давыдов, Т. П. Злыднева // Вестник науки и образования Северо-Запада России: электронный журнал, 2015. – Т. 1. – № 4. – URL: http://vestnik-nauki.ru/ (дата обращения: 30.10.2016).
  9. Ахиезер А. И. Квантовая электродинамика / А. И. Ахиезер, В. Б. Берестецкий. – М.: Наука, 1981. – 432 с.
  10. Davydov A. Modeling of short-pulse laser radiation in terms of photon wave function in coordinate representation [Electronic resource] / A. Davydov, T. Zlydneva // Instrumentation engineering, electronics and telecommunications – 2015: Paper book of the International Forum IEET-2015. – P. 51–63. – Izhevsk: Publishing House of Kalashnikov ISTU, 2016. – 208 p. – 7 MB. – URL: http://pribor21.istu.ru/proceedings/IEET-2015.pdf (accessed: 30.10.2016).
  11. Давыдов А. П. О снижении скорости свободных фотонов при моделировании их распространения в пространстве с помощью волновой функции в координатном представлении [Электронный ресурс] / А. П. Давыдов, Т. П. Злыднева // Труды XIII междунар. научно-технической конф. АПЭП – 2016. – Том 8. – Новосибирск. – 2016. – С. 50–57. – URL: https://cloud.mail.ru/public/FBMT/KugeZk8F7/ТОМ08.pdf (дата обращения: 30.10.2016).
  12. Davydov A. P., Zlydneva T. P. The Young’s interference experiment in the light of the single-photon modeling of the laser radiation [Electronic resource] // Information Technologies in Science, Management, Social Sphere and Medicine (ITSMSSM 2016). – 2016. – P. 208–215. – URL: http://www.atlantis-press.com/php/pub.php?publication=itsmssm-16 (accessed: 30.10.2016).
  13. Давыдов А. П. О релятивистской инвариантности уравнения непрерывности в квантовой механике фотона / А. П. Давыдов, Т. П. Злыднева // Международный научно-исследовательский журнал. – 2016. – №4 (46). – Часть 6. – С. 134–137. doi: 10.18454/IRJ.2016.46.145
  14. Давыдов А. П. Линеаризация волновых уравнений для потенциалов свободного электромагнитного поля с целью его квантовомеханического описания / А. П. Давыдов // Проблемы физ.-мат. образования в педагогич. вузах России на соврем. этапе: тез. докл. межвуз. науч.-практич. конф. / Магнитогорский гос. пед. ин-т. Магнитогорск: МГПИ, 1996. – С. 116–120.

Список литературы на английском языке / References in English

  1. Landau L. Quantenelectrodynamik im Konfigurationsraum / L. Landau, R. Peierls // Zeit. F. Phys. – 1930. – V. 62. – P. 188–198.
  2. Bialynicki-Birula I. On the wave function of the photon / I. Bialynicki-Birula // Acta Phys. Pol. A. – 1994. – V. 86. – P. 97–116.
  3. Sipe J. Photon wave functions // Phys. Rev. A. – 1995. – V. 52. – P. 1875.
  4. Davydov A. P. Kvantovaja mehanika fotona [Photon quantum mechanics] / A. P. Davydov // NAUKA I ShKOLA: tez. dokl. XXXIII nauch. konf. MGPI [SCIENCE AND SCHOOL: abstracts of XXXIII conf. of the Magnitogorsk State Pedag. Inst]. – Magnitogorsk: Izdatelstvo MGPI, 1995. – P. 206–207. [in Russian]
  5. Davydov A. P. Volnovaja funkcija fotona v koordinatnom predstavlenii [The photon wave function in the coordinate representation] / A. P. Davydov // Vestnik MaGU: Periodicheskij nauchnyj zhurnal. Vyp. 5. Estestvennye nauki [MaSU Bulletin: Periodic Scientific Journal. Issue 5. Natural sciences]. – Magnitogorsk: Izdatelstvo MaSU, 2004. – P. 235–243. [in Russian]
  6. Davydov A. P. Kvantovaja mehanika fotona: volnovaja funkcija v koordinatnom predstavlenii [Photon quantum mechanics: the wave function in the coordinate representation] / A. P. Davydov // Jelektromagnitnye volny i jelektronnye sistemy [Electromagnetic waves and electronic systems]. – 2015. – V. 20. – № 5. – P. 43–61. [in Russian]
  7. Davydov A. P. Volnovaja funkcija fotona v koordinatnom predstavlenii [The photon wave function in the coordinate representation] / A. P. Davydov /. – Magnitogorsk: Nosov MSTU, 2015. – 180 P. [in Russian]
  8. Davydov A. P. Odnofotonnyj podhod k modelirovaniju korotkoimpul'snogo lazernogo izluchenija [Single-photon approach to the modeling short-pulse laser radiation] [Electronic resource] / A. P. Davydov, T. P. Zlydneva // Vestnik nauki i obraz. Severo-Zapada Rossii: jelektr. Zhurnal [Bulletin of Science and Education of North-West Russia: electronic journal], 2015. – V. 1. – № 4. – URL: http://vestnik-nauki.ru/ (accessed: 03.10.2016). [in Russian]
  9. Ahiezer A. I. Kvantovaja jelektrodinamika [Quantum electrodynamics] / A. I. Ahiezer, V. B. Beresteckij. – M.: Nauka, 1981. – 432 P. [in Russian]
  10. Davydov A. Modeling of short-pulse laser radiation in terms of photon wave function in coordinate representation [Electronic resource] / A. Davydov, T. Zlydneva // Instrumentation engineering, electronics and telecommunications – 2015: Paper book of the International Forum IEET-2015. – P. 51–63. – Izhevsk: Publishing House of Kalashnikov ISTU, 2016. – 208 p. – 7 MB. – URL: http://pribor21.istu.ru/proceedings/IEET-2015.pdf (accessed: 30.10.2016).
  11. Davydov A. P. On the reduction of free photons speed in modeling of their propagation in space by the wave function in coordinate representation [Electronic resource] / A. P. Davydov, T. P. Zlydneva // 2016 13th International scientific-technical conference on actual problems of electronic instrument engineering (APEIE) – 39281 proceedings – V. 8. – Novosibirsk. – 2016. – P. 50–57. – URL: https://cloud.mail.ru/public/FBMT/KugeZk8F7/ТОМ08.pdf (accessed: 30.10.2016). [in Russian]
  12. Davydov A. P. The Young’s interference experiment in the light of the single-photon modeling of the laser radiation [Electronic resource] / A. P. Davydov, T. P. Zlydneva // Information Technologies in Science, Management, Social Sphere and Medicine (ITSMSSM 2016). – 2016. – P. 208–215. – URL: http://www.atlantis-press.com/php/pub.php?publication=itsmssm-16 (accessed: 30.10.2016).
  13. Davydov A. P., Zlydneva T. P. O reljativistskoj invariantnosti uravnenija nepreryvnosti v kvantovoj mehanike fotona [On the relativistic invariance of the continuity equation in photon quantum mechanics] // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Research Journal]. – 2016. – №4 (46). – Part 6. – P. 134–137. doi: 10.18454/IRJ.2016.46.145 [in Russian]
  14. Davydov A. P. Linearizacija volnovyh uravnenij dlja potencialov svobodnogo jelektromagnitnogo polja s cel'ju ego kvantovomehanicheskogo opisanija [The linearization of the wave equations for the free electromagnetic field potentials with a view to its quantum-mechanical description] / A. P. Davydov // Problemy fiz.-mat. obrazovanija v pedagogich. vuzah Rossii na sovrem. jetape: tez. dokl. mezhvuz. nauch.-praktich. konf. [Problems of phys.-mathematical education in pedagogical universities of Russia at the present stage: abstracts interuniversity scientific-practical conf.] / Magnitogorskij gos. ped. in-t [Magnitogorsk State pedagogical Institute]. Magnitogorsk: MGPI, 1996. – P. 116–120. [in Russian]