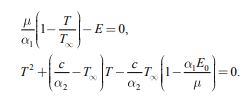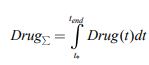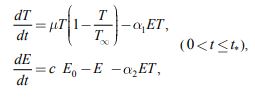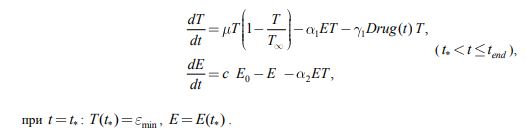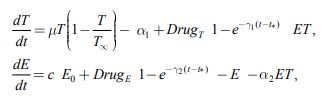МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЛЕЧЕНИЯ ОНКОЛОГИЧЕСКОГО ЗАБОЛЕВАНИЯ
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЛЕЧЕНИЯ ОНКОЛОГИЧЕСКОГО ЗАБОЛЕВАНИЯ
Научная статья
Гончарова А.Б.1, *, Василевская Е.В.2, Колпак Е.П.3, Виль М.Ю.4
1, 2, 3, 4 Санкт-Петербургский государственный университет, Санкт-Петербург, Россия
* Корреспондирующий автор (a.goncharova[at]spbu.ru)
АннотацияРазработаны математическая модель роста новообразование с учетом иммунного ответа организма. Математические модели лечения включают в себя химиотерапию, внешнее вмешательство и иммунотерапию. Математические модели основываются на задаче Коши для обыкновенных дифференциальных уравнений. Проводится анализ стационарных состояний, получены условия «уничтожения» новообразования. Для построения распределения условных больных по стадиям заболевания и продолжительности лечения разработана имитационная модель. Построены зависимости «доза-эффект» для различных программ лечения.
Ключевые слова: математическое моделирование, новообразование, устойчивость, модели лечения, заболеваемость.
MATHEMATICAL MODELING OF CANCER TREATMENT
Research article
Goncharova A.B.1, *, Vasilevskaya E.V.2, Kolpak E.P.3,Vil M.Yu.4
1, 2, 3, 4 Saint Petersburg State University, Saint Petersburg, Russia
* Corresponding author (a.goncharova[at]spbu.ru)
Abstract The current study develops a mathematical model of neoplasm growth taking into account the immune response of the body. Mathematical models of treatment include chemotherapy, external intervention and immunotherapy. Mathematical models are based on the Cauchy problem for ordinary differential equations. The authors conduct an analysis of stationary states and obtain the conditions for the "destruction" of the neoplasm. The study also introduces a model for the purposes of constructing the distribution of conditional patients according to the stages of the disease and the duration of treatment. The "dose-effect" dependencies for various treatment programs are also constructed. Keywords: mathematical modeling, neoplasm, resistance, treatment models, morbidity. ВведениеОнкологические заболевания являются трудно излечимыми, имеют высокую смертность, низкий уровень дожития после лечения [1], [2]. Терапевтические методы лечения не являются эффективными в силу появления на стадии длительного лечения клонов опухолевых клеток, не реагирующих на вводимые препараты, а хирургические – в силу практической невозможности удалить все клетки опухоли [3], [4]. Из небольшого количества мутированных клеток после лечения со временем может вырасти опухоль угрожающих жизни размеров. Существующие терапевтические методы лечения подразумевают несколько последовательных курсов, в каждом из которых в организм вводятся последовательно через заданные промежутки времени препараты [5]. Набор лечебных препаратов, последовательность их введения, временные интервалы внутри курсов лечения и между курсами определяются на основе рандомизированных исследований. Однако, несмотря на постоянное внедрение новых лечебных препаратов, и методов лечения время дожития и распределение больных по стадиям заболевания после лечения за последние 30 лет практически не изменились. Не изменились и локализации заболеваний: у женщин на первом месте стоят заболевания репродуктивной системы, а у мужчин – легких и бронхов. В связи с этим одним из методов анализа развития заболевания с теоретической проработкой возможных вариантов лечения является математическое моделирование [6].
В организме может возникнуть клетка, у которой нарушен механизм самоликвидации [6], [7]. У ее дочерних клеток этот механизм тоже будет нарушен. Эти клетки (опухолевые клетки) из организма не выносятся, они начинают разрастаться в организме, образуя новообразование. По достижении определенного размера (для каждой опухоли он свой) клетки опухоли начинают вызывать серьезные нарушения в организме, приводящие к заболеваниям. Надзор за нормальной работой организма ведет иммунная система. Если проявляются какие-то нарушения в работе отдельных органов или появляются в организме «чужие» вещества, иммунная система включает механизмы ликвидации нарушений [6], [7].
В клинической практике введены четыре стадии заболевании: I, II, III, IV [1], [2]. Первая стадия считается наиболее легкой, четвертая – наиболее тяжелой и опасной. В России основными методами лечения онкологических заболевания являются – хирургический, лучевой, комбинированный [2]. Химиотерапия разной степени дозировки и продолжительности применяется при лечении заболеваний всех стадий [2].
Математическая модель
Математическая модель учитывает два типа клеток опухолевые (делящиеся) клетки и клетки иммунной системы (эффекторные клетки). Рост делящихся клеток происходит в функциональном пространстве (пространстве роста) заданного размера. Кинетика роста популяции делящихся клеток описывается кинетикой Ферхюльста [8]. После заполнения пространства роста полностью делящимися клетками рост их численности прекращается. В начальный момент времени в пространстве роста новообразования появляется небольшое количество делящихся клеток. Иммунная система реагирует на их появление, начинает уничтожать делящиеся клетки при непосредственном контакте с ними.
Пусть Т ‑ количество делящихся клеток, Е ‑ количество эффекторных клеток иммунной системы. Тогда, с учетом гипотезы само регулируемого роста делящихся клеток и их одновременного уничтожения эффекторными клетками, динамика взаимодействия двух типов клеток описывается системой дифференциальных уравнений:
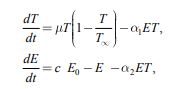 |
(1) |
Система уравнений (1) имеет две неподвижные точки.
- В точке Т=0, Е=Е0 оба собственных значения
матрицы Якоби правой части системы уравнений (1) будут отрицательными, если выполняется неравенство
‑ при высоких скоростях уничтожения делящихся клеток (при больших значениях параметра ) или при большом числе эффекторных клеток. В основной гипотезе естественной история роста опухоли считается, что нулевое состояние неустойчивое [7], [9].
- Вторая неподвижная точка является корнем системы алгебраических уравнений
Если выполняется неравенство ![]() , то эта система уравнений будет иметь единственное решение в первом ортанте плоскости ( Т, Е), при этом первая точка ( Т=0, Е=Е0) будет неустойчивой. Решение будет удовлетворять условиям:
, то эта система уравнений будет иметь единственное решение в первом ортанте плоскости ( Т, Е), при этом первая точка ( Т=0, Е=Е0) будет неустойчивой. Решение будет удовлетворять условиям: ![]() . Таким образом в этой модели в функциональном пространстве содержание эффекторных клеток по сравнению с их количеством в отсутствие делящихся клеток понижается, а количество делящихся клеток будет меньше, чем емкость функционального пространства. При большом количестве эффекторных клеток (при
. Таким образом в этой модели в функциональном пространстве содержание эффекторных клеток по сравнению с их количеством в отсутствие делящихся клеток понижается, а количество делящихся клеток будет меньше, чем емкость функционального пространства. При большом количестве эффекторных клеток (при ![]() ) делящиеся клетки погибают.
) делящиеся клетки погибают.
Собственные значения матрицы Якоби
в этой стационарной точке будут иметь отрицательные вещественные части, если ее определитель
будет положительным. Поскольку рассматривается вариант выполнения неравенства
то положительность определителя матрицы J обеспечивается неравенствомТаким образом, при выполнении неравенства ![]() стационарная точка системы уравнений (1) в зависимости от значений параметров
стационарная точка системы уравнений (1) в зависимости от значений параметров ![]() может быть как устойчивым узлом, так и устойчивым фокусом.
может быть как устойчивым узлом, так и устойчивым фокусом.
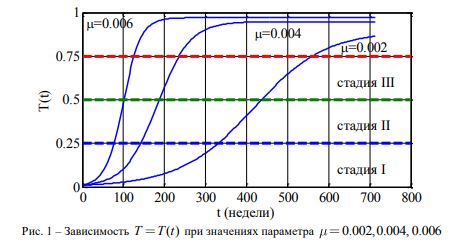
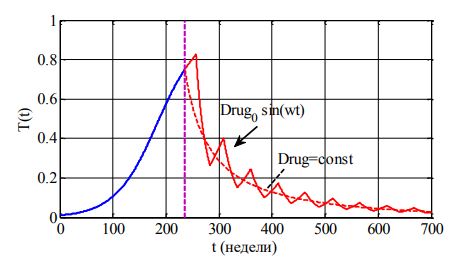
Аналитическое решение уравнений (1) построить не представляется возможным. Анализ решений осуществляется с использованием численных методов. На рис. 1 отражено изменение функции T(t) при значениях параметров: ![]() . Горизонтальными пунктирными линиями отмечены границы раздела между стадиями заболевания. Выбранные значения параметра согласуются с периодами удвоения популяции опухолевых клеток при заболеваниях репродуктивной системы женщин [2], [7], [10] и раке легких у мужчин (от 100 до 360 дней) [2], [3]. Как следует из анализа полученных результатов, при периоде удвоениях опухоли около 180 дней вторая стадия заболевания может быть достигнута за 1-2 года от его начала.
. Горизонтальными пунктирными линиями отмечены границы раздела между стадиями заболевания. Выбранные значения параметра согласуются с периодами удвоения популяции опухолевых клеток при заболеваниях репродуктивной системы женщин [2], [7], [10] и раке легких у мужчин (от 100 до 360 дней) [2], [3]. Как следует из анализа полученных результатов, при периоде удвоениях опухоли около 180 дней вторая стадия заболевания может быть достигнута за 1-2 года от его начала.
Имитационная модель
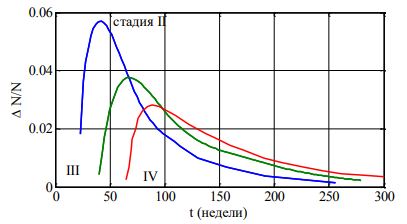
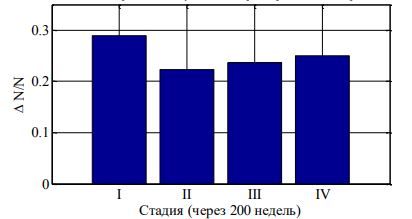
Физические характеристики действительного больного индивидуальны, изменяются от больного к больному в некотором диапазоне. Это позволяет набор параметров в модели (1) сопоставлять с конкретным больным, а выбирая их из заданного диапазона случайным образом смоделировать распределение «больных» по времени наступления второй, третьей и четвертой стадий «заболевания». На рис. 2 приведены такие распределения для N=10000 «больных» для параметров системы уравнений (1), выбираемых случайным образом из диапазонов:На рис. 3 приведен вариант распределения «больных» по стадиям через 200 недель заболевания. По данным Популяционного ракового регистра [2] на текущий момент (2020 г.) около 50% реальных заболеваний репродуктивной системы женщин приходятся на первую и вторую стадии заболевания. То есть расчетные данные для 200 недель заболевания (рис. 3) согласуются с данными ракового регистра.
Рис. 2 – Распределение «больных» по времени наступления второй, третьей и четвертой стадий «заболевания»
Рис. 3 – Распределение «больных» по стадиям через 4 года «заболевания»
Модель химиотерапии
В модель (1) лечение вводится в том случае, если ![]() , поскольку в противном случае иммунная система ликвидирует делящиеся клетки. В модели предполагается, что препараты вводятся в пространство роста по заданной программе лечения, внутри пространства роста уничтожают делящиеся клетки при взаимном контакте, часть препаратов, не вступая в реакцию взаимодействия с делящимися клетками, распадается [5]. С учетом этих предположений модель химиотерапии принимает вид
, поскольку в противном случае иммунная система ликвидирует делящиеся клетки. В модели предполагается, что препараты вводятся в пространство роста по заданной программе лечения, внутри пространства роста уничтожают делящиеся клетки при взаимном контакте, часть препаратов, не вступая в реакцию взаимодействия с делящимися клетками, распадается [5]. С учетом этих предположений модель химиотерапии принимает вид
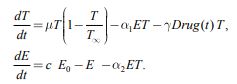 |
(2) |
Суммарное количество расходуемых препаратов подсчитывается по формуле
Лечение состоит из нескольких курсов, каждый из которых имеет заданную продолжительность [5]. В полихимиотерапии при реализации курса применяются несколько препаратов. Продолжительность курса зависит от вида заболевания и применяемых препаратов, может составлять от 3-5 до 30 и более суток [5]. Общее количество курсов может быть более 12. Поскольку каждый курс состоит из применения чередующихся препаратов, поступающих в пространство роста в одном и тоже количестве, то можно принять, что на всем временном промежутке лечения подается одно и то же количество препаратов. С учетом этого предположения принимается, что в (2)
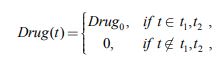 |
(3) |
где t1‑ момент времени начала лечения, а t2‑ момент времени окончания лечения, Drug0 ‑ количество вводимых препаратов в единицу времени.
С учетом этого из первого уравнения в (2) следует, условие «эффективности» препаратов
Это неравенство будет удовлетворяться при больших значениях Drug0 (при большом количестве вводимых препаратов), или при больших значениях параметра y (при высоких скоростях уничтожения делящихся клеток).
Периодическому введению препаратов соответствует функция
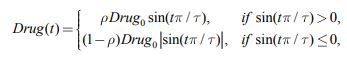 |
(4) |
где ![]() , ‑ продолжительность введения препаратов. Введение параметра p позволяет программу введения препаратов (4) рассматривать как полихимиотерапию, представленную двумя чередующимися во времени препаратами разной эффективности.
, ‑ продолжительность введения препаратов. Введение параметра p позволяет программу введения препаратов (4) рассматривать как полихимиотерапию, представленную двумя чередующимися во времени препаратами разной эффективности.
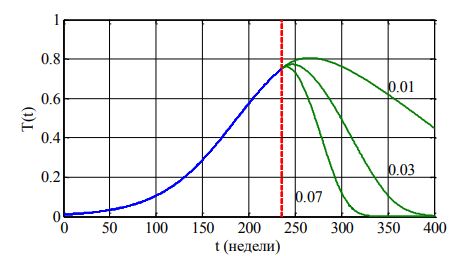
На рис. 4 отражено изменение T(t) («периодическая» зависимость) для случая программы p=1 (4) для , а закону (3) соответствует пунктирная линия. Подача препаратов начиналась в момент достижения третей стадии «заболевания» (в момент времени t=t* достижения T(t)= T(t*)=0.75). Подача препаратов прекращалась при достижении количества делящихся клеток значения меньше, чем ![]() . Суммарное количество препаратов, необходимое для достижения значения Ediag, в обоих случаях одинаковое.
. Суммарное количество препаратов, необходимое для достижения значения Ediag, в обоих случаях одинаковое.
Рис. 4 – Зависимость от времени T(t)
Примечание: момент начала введения препаратов отмечен вертикальной пунктирной линией
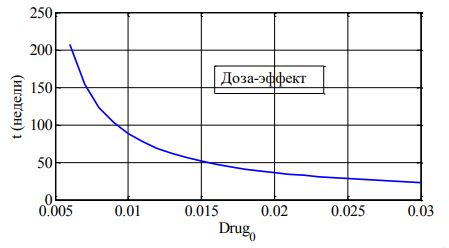
Рис. 5 – Зависимость длительности «лечения» от вводимой постоянно дозы препаратов (от Drug0)
Зависимости «доза-эффект» для программ (3) и (4) для значений ![]() практически не отличается от результата, при условии одинакового количества расходованных препаратов (рис. 4, 5).
практически не отличается от результата, при условии одинакового количества расходованных препаратов (рис. 4, 5).
Как следует из сопоставления различных вариантов функции Drugt общее количество препаратов, расходуемых для достижения заданного значения Ediag, практически одинаковое: общий расход препаратов и продолжительность лечения связаны линейной зависимостью. «Стоимость» лечения пропорциональна количеству введенных препаратов. Наиболее целесообразным для сокращения продолжительности лечения, как это следует из результатов моделирования, давать высокие дозы препаратов на начальном этапе «лечения».
Модель хирургии
Внешнее вмешательство в клинической практике сводится к удалению опухоли на момент постановки диагноза. Однако, как показывает практика, через некоторое время после удаления опухоли может начаться ее новый рост [3]. Поэтому после внешнего вмешательства может назначаться длительное медикаментозное лечение. Это учитывается и в модели внешнего вмешательства.
Пусть рост числа делящихся клеток описывается системой уравнений (1). Пусть в момент времени t=t* , когда количество делящихся клеток достигло значения T= Tt(t*)=T* , происходит «внешнее» вмешательство, приводящее к уменьшению численности делящихся клеток до значения Tt<emin, где emin минимальное количество клинически определимых делящихся клеток. С учетом этих предположений математическая модель внешнего вмешательства в процесс динамики делящихся клеток принимает вид:
приПредполагается, что после внешнего вмешательства (ликвидировано количество клеток) остается количество клеток, которые удаляются за счет химиотерапии (на практике - медикаментозное лечение).
Имитационное моделирование осуществлялось для N=10000«больных» с выбором параметров e и Drug0 случайным образом из диапазонов: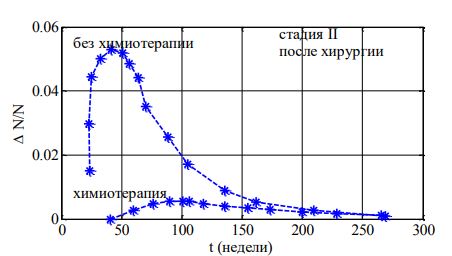
Рис. 6 – Распределение «больных» по времени наступления стадии II после внешнего вмешательства
Примечание: 75% из 5000 вылечиваютсяИммунотерапия
Рост злокачественных новообразований может сопровождаться нарушениями иммунного ответа. Степень подавления иммунного ответа зависит от размера опухоли и проводимого лечения. Эти клинические данные легли в основу разработки методов иммунотерапии в лечении злокачественных новообразований. С этой целью используются в терапевтических дозах различные препараты, восстанавливающие и повышающие активность иммунной системы [11].
В рамках модели (1) иммунотерапия рассматривается как увеличение скорости уничтожения делящихся клеток эффекторными (увеличение параметра ) и как увеличение количества эффекторных клеток (увеличение E0):
где y1 и y2 параметры, характеризующие скорость увеличения активности эффекторных клеток и активности их генерации иммунной системой, соответственно. DrugT‑ количество препаратов, повышающих активность эффекторных клеток, а DrugE‑ повышающих их количество, t*‑ момент времени начала иммунотерапии. В модели предполагается, что активность эффекторных клеток не может стать выше значения ![]() , а максимальное количество эффекторных клеток, которое может выработать иммунная система, не превышает значения
, а максимальное количество эффекторных клеток, которое может выработать иммунная система, не превышает значения ![]() .
.
На рис. 7 приведены зависимости T(t) для случая DrugT = 0.01 , 0.03, 0.07, DrugE =0, y1=1. Вертикальной пунктирной линией отмечен момент начала иммунотерапии. Как следует из анализа полученных результатов влияние параметра DrugE на зависимости, приведенные на рис. 7, незначительно: отклонения составляют не более 5%. Зависимость «доза-эффект» в исследуемом диапазоне параметров совпадает с аналогичной зависимостью для химиотерапии (рис. 5). Соответственно и время достижения заданного результата пропорционально количеству введенных препаратов. В рамках рассмотренной модели иммунотерапии следует считать более эффективным не увеличение общего количества эффекторных клеток, а увеличение их активности.
Рис. 7 – Зависимость T= Tt от времени для DrugT = 0.01 , 0.03, 0.07 при иммунотерапии
Примечание: момент начала введения препаратов отмечен вертикальной пунктирной линией
Заключение
Разработанные модели лечения растущего новообразования на основе обыкновенных дифференциальных уравнений позволяют дать прогноз о распределении больных по стадиям заболевания и времени достижения соответствующих стадий. Модели лечения – химиотерапия и иммунная терапия дают близкие результаты по продолжительности лечения и по зависимости «доза-эффект». При этом на продолжительность «лечения» при заданном расходе препаратов программа лечения может существенное влияние и не оказывать. Для внешнего вмешательства наиболее рациональным является закрепление его результатов медикаментозным лечением.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Мерабишвили В.М. Онкологическая статистика (традиционные методы, новые информационные технологии): Руководство для врачей / В.М. Мерабишвили. Часть I. СПб: 2015. - 223 с.
- Состояние онкологической помощи населению России в 2014 году. М.: МНИОИ им. П.А. Герцена филиал ФГБУ «НМИРЦ» Минздрава России, 2015. - 236 с.
- Кижаев Е.В. Рак легкого. Клиника, диагностика, лечение / Е.В. Кижаев, В.И. Борисов, А.В. Столбовой и др. Издательский дом Бином, М., 2020. - 144 с.
- Переводчикова Н.И. Общие свкедения о клинической химиотерапии / Н.И. Переводчикова //Руководство по химиотерапии опухолевых заболеваний. М.: Практическая медицина, 2013. - С. 21-28с.
- Chu E. Physicians cancer chemotherapy drug manual / E. Chu, V.T. DeVita V. 2007. Jones and Bartlett publishers. Boston, 2007. - 455 p.
- Pang L. Mathematical Modelling and Analysis of the Tumor Treatment Regimens with Pulsed Immunotherapy and Chemotherapy / L. Pang, Z. Shen Long Zhao // Computational and Mathematical Methods in Medicine. - 2016. - ID 6260474. - 12p. DOI: 10.1155/2016/6260474.
- Моисеенко В.М. «Естественная история» роста рака молочной железы / В.М. Моисеенко // Лекции по фундаментальной и клинической онкологии. СПб.: ООО «Издательство Н-Л», 2004. - С. 198-212.
- Parthasakha Das Sayan Mukherjee. An investigation on Michaelis - Menten kinetics based complex dynamics of tumor - immune interaction / Parthasakha Das Sayan Mukherjee, Pritha Das // Chaos, Solitons and Fractals. - 2019. - V. 128. - 297–305. DOI: 10.1016/j.chaos.2019.08.006.
- Варфоломеев С.Д. Неустойчивость нулевого стационарного состояния – фундаментальная проблема ингибирования злокачественного клеточного роста / С.Д. Варфоломеев, А.В. Луковенков // Журнал физической химии. - 2018. - Т. 92. - № 7. - с. 1176–1182. DOI: 10.7868/S
- Kolpak E. P. Neoplasm Morbidity among the Population of Russia / E. P. Kolpak, I. S. Frantsuzova, K. V. Kuvshinova // International journal of advanced biotechnology and research. - 2017. - V.8. - № 3. – P. 2315–2322.
- Царев И.Л. Обзор подходов к иммунотерапии в онкологии / И.Л. Царев, А.В. Мелерзанов //Исследования и практика в медицине. – 2017. - 4(3): 51-65.DOI: 10.17709/2409-2231-2017-4-3-5.
Список литературы на английском языке / References in English
- Merabishvili V.M. Onkologicheskaja statistika (tradicionnye metody, novye informacionnye tehnologii): Rukovodstvo dlja vrachej. [Oncological Statistics (Traditional Methods, New Information Technologies): A Guide for Doctors. Part I.] / M. Merabishvili. - SPb: 2015. - p. 223 [in Russian]
- Sostojanie onkologicheskoj pomoshhi naseleniju Rossii v 2014 godu [The State of Oncological Care to the Population of Russia in 2014]. M.: MNIOI im. P.A. Gercena filial FGBU «NMIRC» Minzdrava Rossii, 2015. - p. 236 [in Russian]
- Kizhaev E.V. Rak legkogo. Klinika, diagnostika, lechenie. [Lung Cancer. Clinic, Diagnosis, Treatment.] / E.V. Kizhaev, V.I. Borisov, A.V. Stolbovoj et al. – Publishing house Binom, M., 2020. - p. 144 [in Russian]
- Perevodchikova N.I. Obshhie svkedenija o klinicheskoj himioterapii [General Information About Clinical Chemotherapy] / N.I. Perevodchikova // Rukovodstvo po himioterapii opuholevyh zabolevanij [Guidance for Chemotherapy of Tumor Diseases]. M.: Prakticheskaja medicina, 2013. - pp. 21-28 [in Russian]
- Chu E. Physicians cancer chemotherapy drug manual / E. Chu, V.T. DeVita V. 2007. Jones and Bartlett publishers. Boston, 2007. - 455 p.
- Pang L. Mathematical Modelling and Analysis of the Tumor Treatment Regimens with Pulsed Immunotherapy and Chemotherapy / L. Pang, Z. Shen Long Zhao // Computational and Mathematical Methods in Medicine. - 2016. - ID 6260474. - 12p. DOI: 10.1155/2016/6260474.
- Moiseenko V.M. «Estestvennaja istorija» rosta raka molochnoj zhelezy [“Natural History” of Breast Cancer Growth] / V.M. Moiseenko // Lekcii po fundamental'noj i klinicheskoj onkologii [Lectures on Fundamental and Clinical Oncology]. SPb.: OOO « Publishing house N-L», 2004. - pp. 198-212. [in Russian]
- Parthasakha Das Sayan Mukherjee. An investigation on Michaelis - Menten kinetics based complex dynamics of tumor - immune interaction / Parthasakha Das Sayan Mukherjee, Pritha Das // Chaos, Solitons and Fractals. - 2019. - V. 128. - 297–305. DOI: 10.1016/j.chaos.2019.08.006.
- Varfolomeev S.D. Neustojchivost' nulevogo stacionarnogo sostojanija – fundamental'naja problema ingibirovanija zlokachestvennogo kletochnogo rosta [Instability of the Zero Stationary State – The Fundamental Problem of Inhibition of Malignant Cell Growth] / S.D. Varfolomeev, A.V. Lukovenkov // Zhurnal fizicheskoj himii [Journal of Physical Chemistry]. - 2018. - Vol. 92. - № 7. - pp. 1176–1182. DOI: 10.7868/S0044453718070221. [in Russian]
- Kolpak E. P. Neoplasm Morbidity among the Population of Russia / E. P. Kolpak, I. S. Frantsuzova, K. V. Kuvshinova // International journal of advanced biotechnology and research. - 2017. - V.8. - № 3. – P. 2315–2322.
- Carev I.L. Obzor podhodov k immunoterapii v onkologii. Issledovanija i praktika v medicine. [Review of Approaches to Immunotherapy in Oncology. Research and Practice in Medicine.] / I.L. Carev, A.V. Melerzanov // 2017. - 4(3): 51-65.DOI: 10.17709/2409-2231-2017-4-3-5. [in Russian]