Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАСПРОСТРАНЕНИЯ ПЛЕНОЧНОГО РЕЖИМА КИПЕНИЯ

Научная статья
Вдовин С.И.
Харитонова И.Ю.
Выпуск: № 10 (29), 2014
Опубликована:
2014/11/08
PDF

Вдовин С.И.1, Харитонова И.Ю.2

1Кандидат технических наук, доцент, Нижегородский государственный технический университет им. Р.Е.Алексеева; 2кандидат технических наук, доцент, Нижегородский государственный технический университет им. Р.Е.Алексеева

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАСПРОСТРАНЕНИЯ ПЛЕНОЧНОГО РЕЖИМА КИПЕНИЯ

Аннотация

В статье построена математическая модель для расчета бегущей тепловой волны, преобразующей пузырьковый режим кипения в пленочный на поверхности тепловыделяющего элемента. Проведены контрольные расчеты, позволяющие установить ограничения на минимальный шаг по пространственной координате.

Ключевые слова: математическое моделирование, режим кипения, численный алгоритм.

Vdovin S.I.1, Kharitonova I.Yu.2

1Candidate of Sciences in Technics, assosiate professor, Nizhny Novgorod State Technical University n.a. R.E. Alekseev, 2Candidate of Sciences in Technics, assosiate professor, Nizhny Novgorod State Technical University n.a. R.E. Alekseev

MATHEMATICAL MODEL OF THE FILM BOILING DISTRIBUTION

Abstract

In the article a mathematical model is constructed for calculation of the running heat wave that transforms the bubble boiling into the  film boiling on the surface of a fuel element. Control calculations are carried out that allow to set limits on the minimum step in the spatial coordinate.

Keywords: mathematical modeling, boiling regime, numerical algorithm.

Увеличение единичной мощности энергетической установки (ЭУ) лимитируется требованиями надежного отвода тепла из активной зоны (АЗ). Применительно к водо-водяным кипящим реакторам эта проблема тесно связана с ограничениями по кризису теплообмена и с обеспечением устойчивости стационарного режима. При этом главный фактор, препятствующий увеличению уровня мощности реактора, может меняться при изменении режимных параметров ЭУ [1].

В работе [2] при изучении явления перехода пузырькового режима кипения в пленочный (на нагреваемых током нитях и стержнях) было замечено, что смена происходит путем возникновения бегущей тепловой волны, меняющей режим кипения на поверхности тепловыделяющего элемента. Экспериментальный и расчетный анализ изменения теплофизических параметров нити накаливания и устойчивости к локальным возмущениям проводился в [3–6].

В настоящей работе, используя разработанный численный алгоритм, исследуется явление формирования и распространения волны пленочного режима кипения применительно к реальным топливным элементам. Анализируется изменение температурного режима и влияние некоторых конструктивных и режимных параметров на скорость рассматриваемых процессов. Эти вопросы представляют интерес при изучении начальных этапов развития аварий, связанных с перегревом твэлов. Сложность расчета обусловлена сильным разнесением характерных пространственных (температурный фронт ~ 10–3 м, высота АЗ ~ 1 м) и временных (постоянная прогрева горючего ~ 10 с, элемента оболочки твэла ~ 10–2 с) масштабов.

Описание математической модели и алгоритма расчета

Уравнения теплового баланса для горючего и оболочки твэла в одноточечном приближении их описания в поперечном сечении z запишем в виде:

10-09-2020 11-40-56            (1) 10-09-2020 11-41-07      (2)

где T, λ, ρ, c, V – соответственно температура, теплопроводность, плотность, теплоемкость и объем; индексы r и ст соответствуют горючему и оболочке твэла; ψ(z) – пространственная форма тепловыделения; n – амплитуда первой гармоники потока нейтронов тепловой группы; S – площадь поверхности; K – коэффициент теплопередачи от горючего к оболочке твэла; q – плотность теплового потока.

Уравнение (1) не учитывает теплопередачу вдоль горючего. Это оправдано тем, что топливные таблетки разделены зазорами и длина обогреваемой части в 102 ÷ 103 раз превышает поперечный размер твэла.

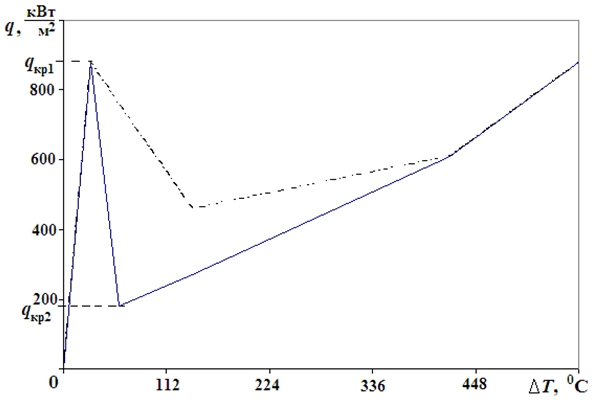
Зависимость плотности теплового потока q от разности температур поверхности нагрева и воды ΔT по опытам С.С.Кутателадзе [7] показана на рис.1. Влияние давления, расхода и паросодержания на значения первой и второй критической плотности теплового потока (qкр1, qкр2) рассмотрено в работах [8, 9]. Отметим некоторые характерные черты функциональной обусловленности теплового потока. В области пузырькового режима кипения интенсивность теплообмена сильно зависит от температурного напора (ΔT), т.е. использование той либо иной функции от теплофизических параметров теплоносителя не приводит к существенному изменению температурного режима теплоотдающей поверхности. Другая характерная черта состоит в том, что в широком диапазоне изменения давления и расхода (принудительная циркуляция) отношение qкр1/qкр2 имеет примерно то же значение, что и при кипении в большом объеме [9]. Это обусловлено гидродинамической природой кризиса теплообмена первого рода. С учетом отмеченных фактов далее при анализе температурного режима в условиях фиксированных значений давления, расхода и энтальпии воды на входе в АЗ будем использовать зависимость теплового потока, показанную на рис. 1.

10-09-2020 12-10-56

Рис.1 - Зависимость плотности теплового потока ( q ) от температурного напора (ΔT = Tст - T): сплошная линия – зависимость по опытным данным С.С.Кутателадзе [7]; пунктирная линия – измененная в диапазоне пленочного кипения зависимость.

 

Так как в настоящей работе не предполагается построение замкнутой системы для исследования ЭУ, то пароводяную смесь будем считать гомогенной термодинамически равновесной средой, движущейся без проскальзывания фаз. При указанных допущениях уравнения сохранения энергии и неразрывности совместно с граничными условиями запишем в виде:

10-09-2020 11-46-23            (3) u(0, t) = u0;                    J(0, t) = J0;                             z ∈ [0, l];           (4)

где u, J, v – скорость, энтальпия и удельный объем теплоносителя;

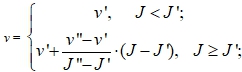
10-09-2020 11-47-12

v’, v’’ – удельный объем воды и пара на линии насыщения;

J’, J’’ – энтальпия воды и пара на линии насыщения;

u0, J0, v’, v’’, J’, J’’  – const;

Q = qS/V – тепловой поток в единицу объема теплоносителя. Зависимость температуры воды от энтальпии будем аппроксимировать кусочно-линейной функцией

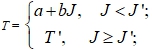
10-09-2020 11-47-41

где a, b – const, определяемые из работы [10] 10-09-2020 11-47-56.

Исследование распространения волны пленочного режима кипения проводилось численным методом на основе математической модели (1) - (4). В области резкого (слабого) изменения температуры теплоотдающей поверхности предусматривалось дробление (объединение) шага сетки по пространственной координате. Величина шага ограничивалась сверху и снизу заданными величинами. Для расчета температуры горючего и теплоносителя использовали равномерные сетки, содержащие соответственно n1 и n2 узлов. Шаг по времени выбирался с учетом характерной постоянной времени исследуемого переходного процесса, т.е. имел различные значения для горючего, оболочки твэла и теплоносителя.

Для проверки точности определения температуры стенки были проведены контрольные расчеты распространения температурного фронта при постоянном и переменном шаге по пространственной координате. Вычисления проводились на элементе малой длины (l = 0.1 м), температура горючего и теплоносителя не изменялась. В качестве исходного возмущения принималось ступенчатое увеличение температуры оболочки на части рассматриваемого элемента. Величина возмущения задавалась достаточной для образования бегущей тепловой волны при перепаде температуры на стенке в стационарном режиме ΔT* = 22.8oС. Скорость распространения температурного фронта определялась по смещению точки с фиксированной температурой, несколько превышающей (≈ 40oC) температуру поверхности, соответствующую пузырьковому режиму кипения.

Показано, что уменьшение постоянного шага разностной сетки с 10–3 м до 5·10–4 м увеличивает расчетную скорость распространения температурного фронта с 5.8·10–3 м/с до 6·10–3 м/с, т.е. вычисления с шагом менее 10–3 м приемлемы для контрольного сравнения. При вычислении с переменным шагом аналогичное снижение ограничения на минимальный шаг разностной сетки уменьшает относительную погрешность с 12% (5.3·10–3 м/с) до значений менее 1% (6·10–3 м/с). Количество узлов разностной сетки в этом варианте сокращается примерно в 10 раз. Таким образом требуемая точность расчетов изменения температуры оболочки достигается с помощью надлежащего выбора ограничения на минимальный шаг по пространственной координате.

Литература

  1. Исследование характеристик кипящего реактора при пониженных давлениях / Р.Е.Федякин, В.Е.Шмелев, Б.В.Кебадзе и др. //Теплоэнергетика. 1979. № 5, с.44-46.
  2. Петухов Б.С., Ковалев С.А. Методика и некоторые результаты измерения критической нагрузки при переходе от пленочного кипения к пузырьковому // Теплоэнергетика. 1962. № 5, с.65-70.
  3. Ковалев С.А., Рыбчинская Г.Б., Вильке В.Г. Об устойчивости теплообмена при кипении к возмущениям конечной величины // ТВТ. 1973. Т.II, № 4. с.805-809.
  4. Жуков С.А., Барелко В.В., Мержанов А.Г. К теории волновых процессов на тепловыделяющих поверхностях при кипении жидкостей // Докл. АН СССР. 1978. Т.242, № 5, с.1064-1067.
  5. Жуков С.А., Барелко В.В., Мержанов А.Г. Динамика перехода между пузырьковым и пленочным кипением в режиме бегущей волны // Докл. АН СССР. 1979, Т.245, № 1, с.94-97.
  6. Жукова Л.А., Жуков С.А., Гельман Е.А. Инициирование автоволнового перехода в пленочный режим кипения путем локального ухудшения теплоотдачи // ТВТ, 1989, Т.27, № 1, с.189-192.
  7. Кутателадзе С.С., Накоряков В.Е. Тепломассообмен и волны в газожидкостных системах. – Новосибирск: Наука, 1984.
  8. Дорощук В.Е. Кризисы теплообмена при кипении воды в трубах. – М.: Энергия, 1970.
  9. Кутепов А.М., Стерман Л.С., Стюшин Н.Г. Гидродинамика и теплообмен при парообразовании: Учеб. пособие для втузов, 3-е изд., испр. – М.: Высш.шк., 1986.
  10. Дементьев Б.А. Ядерные энергетические реакторы: Учебник для вузов. – М.: Энергоатомиздат, 1984.

References

  1. Issledovanie harakteristik kipjashhego reaktora pri ponizhennyh davlenijah / R.E.Fedjakin, V.E.Shmelev, B.V.Kebadze i dr. //Teplojenergetika. 1979. № 5, s.44-46.
  2. Petuhov B.S., Kovalev S.A. Metodika i nekotorye rezul'taty izmerenija kriticheskoj nagruzki pri perehode ot plenochnogo kipenija k puzyr'kovomu // Teplojenergetika. 1962. № 5, s.65-70.
  3. Kovalev S.A., Rybchinskaja G.B., Vil'ke V.G. Ob ustojchivosti teploobmena pri kipenii k vozmushhenijam konechnoj velichiny // TVT. 1973. T.II, № 4. s.805-809.
  4. Zhukov S.A., Barelko V.V., Merzhanov A.G. K teorii volnovyh processov na teplovydeljajushhih poverhnostjah pri kipenii zhidkostej // Dokl. AN SSSR. 1978. T.242, № 5, s.1064-1067.
  5. Zhukov S.A., Barelko V.V., Merzhanov A.G. Dinamika perehoda mezhdu puzyr'kovym i plenochnym kipeniem v rezhime begushhej volny // Dokl. AN SSSR. 1979, T.245, № 1, s.94-97.
  6. Zhukova L.A., Zhukov S.A., Gel'man E.A. Iniciirovanie avtovolnovogo perehoda v plenochnyj rezhim kipenija putem lokal'nogo uhudshenija teplootdachi // TVT, 1989, T.27, № 1, s.189-192.
  7. Kutateladze S.S., Nakorjakov V.E. Teplomassoobmen i volny v gazozhidkostnyh sistemah. – Novosibirsk: Nauka, 1984.
  8. Doroshhuk V.E. Krizisy teploobmena pri kipenii vody v trubah. – M.: Jenergija, 1970.
  9. Kutepov A.M., Sterman L.S., Stjushin N.G. Gidrodinamika i teploobmen pri paroobrazovanii: Ucheb. posobie dlja vtuzov, 3-e izd., ispr. – M.: Vyssh.shk., 1986.
  10. Dement'ev B.A. Jadernye jenergeticheskie reaktory: Uchebnik dlja vuzov. – M.: Jenergoatomizdat, 1984.