К ИССЛЕДОВАНИЮ РОБАСТНОЙ УСТОЙЧИВОСТИ И АПЕРИОДИЧНОСТИ НЕПРЕРЫВНЫХ И ДИСКРЕТНЫХ СИСТЕМ
К ИССЛЕДОВАНИЮ РОБАСТНОЙ УСТОЙЧИВОСТИ И АПЕРИОДИЧНОСТИ НЕПРЕРЫВНЫХ И ДИСКРЕТНЫХ СИСТЕМ
Научная статья
Антоновская О.Г.1, *, Бесклубная А.В.2
1 ORCID: 0000-0002-5688-7996;
1, 2 Нижегородский государственный архитектурно-строительный университет, Нижний Новгород, Россия
* Корреспондирующий автор (olga.antonovsckaja[at]yandex.ru)
АннотацияВ настоящее время нет необходимости обосновывать важность вопроса об исследовании робастной устойчивости (т.е. сохранения системой устойчивости в условиях неопределенности). Если модель описывает физический объект (механический, физический, экономический и т.д.), то, как правило, его параметры неизвестны точно, хотя уравнения, описывающие работу системы, известны. То есть в реальных задачах обязательно присутствует неопределенность. В предлагаемой работе рассматриваются некоторые подходы к исследованию как устойчивости, так и апериодичности интервально неопределенных непрерывных и дискретных систем с использованием критерия Михайлова. Приведены примеры конкретных расчетов границ робастной устойчивости для непрерывных систем третьего и четвертого порядка.
Ключевые слова: интервальная неопределенность, робастная устойчивость, апериодичность, метод D-разбиений, критерий Михайлова.
ON THE STUDY OF ROBUST STABILITY AND APERIODICITY OF CONTINUOUS AND DISCRETE SYSTEMS
Research article
Antonovskaya O.G.1, *, Besklubnaya A.V.2
1 ORCID: 0000-0002-5688-7996;
1, 2 Nizhny Novgorod State University of Architecture and Civil Engineering, Nizhny Novgorod, Russia
* Corresponding author (olga.antonovsckaja[at]yandex.ru)
AbstractAt present, there is no need to justify the importance of the study of robust stability (i.e., the preservation of stability by the system under conditions of uncertainty). If the model describes a physical object (mechanical, physical, economic, etc.), then, as a rule, its parameters are not known exactly, although the equations describing the operation of the system are known. That is, there is always uncertainty in real tasks. The article discusses some approaches to the study of both stability and aperiodicity of interval-indeterminate continuous and discrete systems using the Mikhailov criterion. The study provides examples of concrete calculations of robust stability boundaries for continuous systems of the third and fourth order.
Keywords: interval uncertainty, robust stability, aperiodicity, D-partitioning method, Mikhailov criterion.
Введение
Для сохранения наглядности результатов изучения устойчивости в пространстве параметров многомерных динамических систем целесообразно придерживаться предложенного в [1] подхода, когда вся группа параметров динамической системы делится на две части. К первой части относятся два наиболее важных в приложениях параметра, значения которых выбираются, ко второй части относятся параметры, заданные в фиксированных интервалах. При таком подходе область устойчивости строится на плоскости двух действительных параметров, а интервальность остальных параметров с точки зрения границ области устойчивости приводит к необходимости отыскания внутренней границы семейства границD-разбиения [2, C.86-107] (так называемое робастное D-разбиение [3], [4]). Применение же критериев робастной устойчивости должно позволить учесть не малость интервалов изменения параметров, а следовательно, не малость интервалов изменения коэффициентов характеристического уравнения.
Проблема робастной устойчивости возникает в любых задачах по конструированию и нормальному функционированию технических систем [1], [5], [6], [7]. В реальных задачах (идет ли речь о радиотехнических системах [6, С.7], системах управления космическими аппаратами [6, С.8] или управлении автомобилем [6, С.173]) обязательно присутствует некоторая неопределенность, связанная либо с наличием внешних возмущений, либо с невозможностью точного определения параметров. Поэтому вопросам робастной устойчивости посвящена уже значительная литература [1], [8]. В настоящей работе рассматриваются некоторые подходы к исследованию не только устойчивости, но и апериодичности интервально неопределенных непрерывных и дискретных систем.
Робастная устойчивость и апериодичность непрерывных систем
Известно, что критерий Рауса-Гурвица в аналитическом варианте для систем высокого порядка становится громоздким [6, C.82]. Наглядная оценка влияния изменения параметров на устойчивость при использовании этого критерия затруднена. Для этих целей может оказаться полезным критерий Михайлова [6, C. 78]. При этом свойство наглядности применения критерия Михайлова сохраняется и при решении вопроса о робастной устойчивости [6, C. 188-189].
Пусть необходимо определить условия устойчивости интервального полинома
| (1) |
относительно области . Согласно теореме Харитонова [5], [6, C. 189], необходимые и достаточные условия устойчивости интервального полинома (1) заключаются в устойчивости только четырех полиномов семейства (1) с коэффициентами:
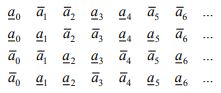 |
(2) |
При этом, очевидно, наглядность применения критерия Михайлова для определения устойчивости интервального полинома (1) определяется наглядностью его применения к четырем полиномам с фиксированными значениями коэффициентов (2). Однако критерий Михайлова может быть применен и непосредственно к исходному интервальному полиному (1). В этом случае процедура получения условий устойчивости становится очевидной.
Действительно, согласно критерию Михайлова изучению подлежит исследование поведения на комплексной плоскости годографов| (3) |
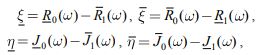 |
(4) |
А черта сверху или снизу у функций R(w) и J(w) переносится на все коэффициенты , входящие в эти функции.
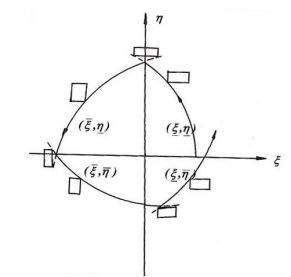
При изменении параметра w прямоугольник П, перемещаясь на плоскостиНа рисунке 1 граница Г изображена сплошной линией. Пунктиром приведены участки годографов, формирующих границу Г в соответствии с приведенным выше правилом выбора вершин прямоугольника П. Для удобства на рисунке рядом с соответствующим участком границы приведены координаты определяющей ее вершины. Заметим, что непосредственно из рисунка 1 следует, что в формировании границы Г участвуют только вершины прямоугольника П. Но так как значения коэффициентов полинома в каждой из вершин прямоугольника определяют все четыре полинома теоремы Харитонова, то это означает, что граница Г может быть получена и на основе анализа относительного поведения годографов этих полиномов.
Рис. 1 – Характер границы и положения прямоугольников
Теперь рассмотрим вопрос об апериодичности интервального полинома (1). Произведем D-разбиение на комплексной плоскости полиномов относительно m-сектора [10]:
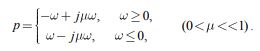 |
(5) |
Тогда Pn(p) можно представить в виде ряда по m и, следовательно, уравнения полученной границы D-разбиение в первом приближении по m будут задаваться уравнениями
| |
(6) |
Пример. Условия устойчивости интервальных полиномов третьего и четвертого порядка для непрерывных систем.
- Пусть характеристический полином непрерывной системы является полиномом третьего порядка
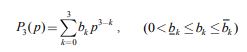 |
(7) |
Для полинома (7) имеем
| |
(8) |
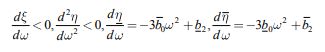 |
(9) |
| |
(10) |
| |
(11) |
Надо заметить, что условие чередования корней здесь выполнено, а условие устойчивости интервального полинома (7) сводится лишь к выполнению (11), т.к. (10) выполняется при выполнении (11).
- Пусть характеристический полином непрерывной системы является полиномом четвертого порядка
| (12) |
Для полинома (12) имеем
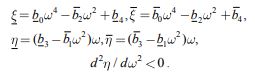 |
(13) |
| |
(14) |
| |
(15) |
| |
(16) |
Некоторые предложения по исследованию робастной устойчивости и апериодичности дискретных систем
Для интервального полинома (1), являющегося характеристическим полиномом для дискретной системы, условием устойчивости является требование расположения всех корней внутри единичного круга. При использовании аналога критерия Михайлова следует отобразить верхнюю часть единичного круга плоскости корней на комплексную плоскость| (17) |
Подобно случаю непрерывных систем, можно решить и вопрос о робастной апериодичности. Действительно, в качестве контура на плоскости корней возьмем m-сектор
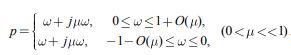 |
(18) |
После подстановки (18) в (1), разложения полученного уравнения в ряд по m и ограничения линейным приближением, приходим к следующим уравнениям семейства границ D-разбиения при ![]() :
:
| (19) |
Для ![]() на комплексной плоскости
на комплексной плоскости ![]() граница D-разбиения будет симметрична относительно оси
граница D-разбиения будет симметрична относительно оси ![]() по сравнению со случаем
по сравнению со случаем ![]() . При
. При ![]() семейство границ D-разбиения прижимается к оси
семейство границ D-разбиения прижимается к оси ![]() , причем интервалы, в которых граница D-разбиения пересекает ось
, причем интервалы, в которых граница D-разбиения пересекает ось ![]() , в пределе задаются величинами
, в пределе задаются величинами ![]() , где, функция Ro содержит коэффициенты полинома с нечетными степенями, а R1 – с четными. Но это означает, что робастная апериодичность полинома имеет место тогда и только тогда, когда два полинома, получающихся из (1) при
, где, функция Ro содержит коэффициенты полинома с нечетными степенями, а R1 – с четными. Но это означает, что робастная апериодичность полинома имеет место тогда и только тогда, когда два полинома, получающихся из (1) при ![]() , апериодичны.
, апериодичны.
В заключение отметим, что полученные для случая характеристических полиномов третьего и четвертого порядка результаты могут быть использованы при исследовании математических моделей реальных систем. Системы дифференциальных уравнений третьего порядка являются, скажем, математическими моделями аутоиммунитета [11], явления конвекции между двумя параллельными горизонтальными пластинами, поддерживаемыми при различных температурах [12, С.18]. Системы дифференциальных уравнений четвертого порядка описывают работу металлорежущих станков [13], часовых механизмов [14] и т.д.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Неймарк Ю. И. Мера робастной устойчивости и робастное D-разбиение / Ю. И. Неймарк. // Динамика систем: Межвуз. сборник – Н. Новгород: Изд-во ННГУ, 1992. – С. 39-55.
- Неймарк Ю. И. Динамические системы и управляемые процессы / Ю. И. Неймарк. – М.: Наука, 1978. – 336 с.
- Неймарк Ю. И. Робастная устойчивость линейных непрерывных, дискретных и распределенных систем / Ю. И. Неймарк. // Динамика систем: Межвуз. сборник – Н. Новгород: Изд-во ННГУ, 1991. – С. 5-20.
- Неймарк Ю. И. Робастная устойчивость и D-разбиение / Ю. И. Неймарк. // Автоматика и телемеханика – 1992. – № 7. – С. 10–18.
- Джури Э.И. Робастность дискретных систем / Э.И. Джури // Автоматика и телемеханика – 1990. – № 5. С.3-28.
- Поляк Б. Т. Робастная устойчивость и управление. / Б. Т. Поляк, П. С. Щербаков. – М.: Наука, 2002. – 303 с.
- Поляк Б. Т. Управление линейными системами при внешних возмущениях. / Б. Т. Поляк, М. В. Хлебников, П. С. Щербаков. – М.: ЛЕНАНД, 2014. – 560 с.
- Оморов Р. О. Чувствительность, робастность и грубость динамических систем / Р. О. Оморов. – М.: ЛЕНАНД, 2021. – 304 с.
- Харитонов В. Л. Об устойчивости положения равновесия семейства систем линейных дифференциальных уравнений. / В. Л. Харитонов // Дифференциальные уравнения. – 1978. – Т. 14. – № 11. – С.2086-2088.
- Горюнов В. И. Построение области апериодической устойчивости линейных дискретных систем по методу D-разбиений / В. И. Горюнов // Известия вузов: Электромеханика. – 1985. – № 12. – С.39-41.
- Минц Р.М. Применение геометрического приема А.А. Андронова к исследованию состояний равновесия в трехмерном пространстве. / Р.М. Минц, Н.С. Чалкова. // Динамика систем: Межвуз. сборник – Горький: Изд-во ГГУ, 1990. – С. 45-54.
- Неймарк Ю. И. Стохастические и хаотические колебания. / Ю. И. Неймарк, П. С. Ланда. – М.: Либроком, 2009. – 424 с.
- Глебская О.Ю. Исследование колебательных явлений в металлорежущих станках / О.Ю. Глебская, В.И. Королев, С.И. Сидорова и др. // Динамика систем: Межвуз. сборник – Н. Новгород: Изд-во ННГУ, 1995. – С. 113-135.
- Глебская О. Ю. Динамика автоколебательной системы при наличии гироскопических сил. / О. Ю. Глебская, В. И. Королев // Динамика систем: Межвуз. сборник – Н. Новгород: Изд-во ННГУ, 1995. – С. 135-153.
Список литературы на английском языке / References in English
- Neymark Yu. I. Mera robastnoy ustoytchivosti i robastnoe D-razbienie [Robust stability measure and D-partitioning] / Yu. I. Neymark. // Dinamika system [System dynamics] – N. Novgorod: Publishing house NNGU, 1992. – P. 39-55. [in Russian]
- Neymark Yu. I. Dinamitcheskie sistemy i upravlyaemye protsessy [Dynamic systems and control processes] / Yu. I. Neymark. – M.: Nauka, 1978. – 336 p. [in Russian]
- Neymark Yu. I. Robastnaya ustoytchivost lineynykh nepreryvnykh, diskretnykh i raspredelennykh sistem [Robust stability of linear continuous, descrete and distributed systems] / Yu. I. Neymark. // Dinamika system [System dynamics] – N. Novgorod: Publishing house NNGU, 1991. – P. 5-20. [in Russian]
- Neymark Yu. I. Robastnaya ustoytchivost i D-razbienie [Robust stability and D-partitioning] / Yu. I. Neymark. // Avtomatika i telemekhanika [Automation and remote control] – 1992. – № 7. – P. 10–18. [in Russian]
- Djury E.I. Robastnost’ diskretnykh sistem [Robustness of discrete systems] / E. I. Djury // Avtomatika i telemekhanika [Automation and remote control] 1990. – № 5. P.3-28. [in Russian]
- Polyak B. T. Robastnaya ustoytchivost i upravleniye [Robust stability and control] / B. T. Polyak, P. S. Sherbakov – M.: Nauka, 2002. – 303 p. [in Russian]
- Polyak B. T. Upravleniye lineynymi sistemami pri vneshnpkh vozmusheniyakh [Control of linear systems over external disturbances] / B. T. Polyak, M. V. Hlebnikov, P. S. Sherbakov – M.: LENAND, 2014. – 560 p. [in Russian]
- Omorov R. O. Chuvstvitel’nost’, robastnost’ i grubost’ sistem [Sensitivity, robustness and roughness of systems] / R. O. Omorov – M.: LENAND, 2014. – 304 p. [in Russian]
- Haritonov V. L. Ob ustoytchivosti polozheniya ravnovesiya seseystva sistem lineynykh differentsial’nykh uravneniy [On stability of the equilibrium of the family of linear differential equations systems] / V. L. Haritonov // Differential equations. – 1978. – V. 14. – № 11. – P.2086-2088. [in Russian]
- Goryunov V. I. Postroeniye oblasti aperioditcheskoy ustoytchivosti lineynykh diskretnykh system po metodu D-razbiyeniy [A-periodic stability region construction for discrete systems by D-partitioning method] / V. I. Goryunov // Izvestiya vuzov: Elektromekhanika. – 1985. – № 12. – P.39-41. [in Russian]
- Mints R. M. Primeneniye geometritcheskogo priyema A. A. Andronova k issledovaniyu sostoyaniy ravnovesiya v trekhmernom prostranstve. [A. A. Andronov geometrical method use for equilibrium study in three-dimensional space] / R. M. Mints, N. S. Chalkova. // Dinamika system [System dynamics] – Gorky: Publishing house GGU, 1990. – P. 45-54. [in Russian]
- Neymark Yu. I. Stokhasticheskiye I khaoticheskiye kolebaniya. [Stochastic and chaotic vibrations] / Yu. I. Neymark, P. S. Landa – M.: Librokom, 2009. – 424 p.[inRussian]
- Glebskaya O. Yu. Issledovaniye kolebatel’nykh yableniy d metallorezhushikh stankakh [Vibration phenomena study in metal-cutting machine] / O. Yu. Glebskaya, V. I. Korolev, S. I. Sidorova et al. // Dinamika system [System dynamics] – N. Novgorod: Publishing house NNGU, 1995. – P. 113-135. [in Russian]
- Glebskaya O. Yu. Dinamika aviokolebatel’noy sistemy pti nalichiyi giroskopitcheskikh sil [Auto-vibrations dynamics under gyroscopic forces] / O. Yu. Glebskaya, V. I. Korolev // Dinamika system [System dynamics] – N. Novgorod: Publishing house NNGU, 1995. – P. 135-153. [inRussian]