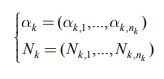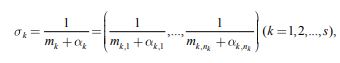ДИФФЕРЕНЦИАЛЬНЫЕ СВОЙСТВА ФУНКЦИЙ
ДИФФЕРЕНЦИАЛЬНЫЕ СВОЙСТВА ФУНКЦИЙ![]()
Научная статья
Гянджинский Государственный Университет, Гянджа, Азербайджан
* Корреспондирующий автор (nneymatov[at]yandex.ru)
АннотацияПервое интегральное представление функций многих переменных, определенных в областях (звездных, относительно точкам некоторого шара) GMEn принадлежит академику С.Л.Соболеву. С.Л.Соболевым разработан метод интегральных представлений функций из построенных им же известных функциональных пространств ![]() и доказаны основные теоремы вложения этих пространств, с дальнейшими приложениями в теорию дифференциальных уравнений в частных производных.
и доказаны основные теоремы вложения этих пространств, с дальнейшими приложениями в теорию дифференциальных уравнений в частных производных.
Дальнейшее развитие метода интегральных представлений теории пространств дифференцируемых функций многих переменных связано с именем В.П.Ильина.Он доказал принципиально новое интегральное представление функций многих переменных в любой точке xOEn.
В работе исследуются «весовые» пространства функций ![]() , точек многих пачек переменных
, точек многих пачек переменных ![]() , определенных в области
, определенных в области
![]() , удовлетворяющих условию «меняющейся
, удовлетворяющих условию «меняющейся ![]() -полурога». Эти построенные «весовые» пространства типа обобщенных B -пространств зависит от параметра
-полурога». Эти построенные «весовые» пространства типа обобщенных B -пространств зависит от параметра ![]() , которые в случае s=1 обобщают известных «весовых» пространств
, которые в случае s=1 обобщают известных «весовых» пространств ![]() -О.В.Бесова, а в случае s=n, обобщают известных пространств
-О.В.Бесова, а в случае s=n, обобщают известных пространств ![]() функций с доминирующей смещенной производной, в случае степенных «весов» приведенных в работах А.Дж.Джабраилова.
функций с доминирующей смещенной производной, в случае степенных «весов» приведенных в работах А.Дж.Джабраилова.
А.Д.Джабраиловым доказаны новые интегральные представления функций многих переменных, с помощью которых ему удалось построить общую теорию пространств функций, с доминирующей смешанной производной![]() , с дальнейшей разработкой метода интегральных представлений в теории теоремы вложения этих пространств.
, с дальнейшей разработкой метода интегральных представлений в теории теоремы вложения этих пространств.
Строится новое функциональное пространство и методом интегральных представлений [1], на основе нового интегрального представления гладких функций в точках ![]() .
.
DIFFERENTIAL PROPERTIES OF THE FUNCTIONS![]()
Research article
Neymatov N.A.*
GanjaState University,Ganja, Azerbaijan
* Corresponding author (nneymatov[at]yandex.ru)
AbstractThe first integral representation of the functions of many variables defined in the regions (star regions relative to the points of a given ball) GMEn belongs to academician S.L. Sobolev. S.L.Sobolev developed a method of integral representations of functions from well-known functional spaces constructed by him ![]() and proved the basic theorems of embedding these spaces with further applications to the theory of partial differential equations.
and proved the basic theorems of embedding these spaces with further applications to the theory of partial differential equations.
Further development of the method of integral representations of the theory of spaces of differentiable functions of many variables is associated with the name of V.P. Ilyin. He proved a fundamentally new integral representation of functions of many variables at any point xOEn.
The study investigates the "weight" spaces of functions ![]() , points of many bundles of variables
, points of many bundles of variables ![]() definedinthedomain satisfyingthecondition "variable
definedinthedomain satisfyingthecondition "variable ![]() -semihorn". These constructed "weight" spaces of the type of generalized B-spaces depend on the parameter
-semihorn". These constructed "weight" spaces of the type of generalized B-spaces depend on the parameter ![]() , which in the case s=1 generalize the known "weight" spaces
, which in the case s=1 generalize the known "weight" spaces ![]() -O.V.Besov, and in the case s=1, generalize the known spaces of
-O.V.Besov, and in the case s=1, generalize the known spaces of ![]() functions with a dominant shifted derivative, in the case of power "weights" given in the works of A.J.Dzhabrailov.
functions with a dominant shifted derivative, in the case of power "weights" given in the works of A.J.Dzhabrailov.
A.D.Dzhabrailov proved new integral representations of functions of many variables, with the help of which he managed to build a general theory of spaces of functions with a dominant mixed derivative ![]() , with further development of the method of integral representations in the theory of the embedding theorem of these spaces.
, with further development of the method of integral representations in the theory of the embedding theorem of these spaces.
A new functional space is also constructed by the method of integral representations [1] based on a new integral representation of smooth functions at points ![]() .
.
Keywords: spaces, whole, vector, semihorns, seminorm.
Пусть задана тройка векторов| |
(1) |
с координатами-векторами ![]() соответственно, при этом предполагаем, что векторы
соответственно, при этом предполагаем, что векторы ![]() являются «целочисленными и неотрицательными», т.е.
являются «целочисленными и неотрицательными», т.е. ![]() -целые, при всех k=1,2,…,s, а вектор
-целые, при всех k=1,2,…,s, а вектор ![]() является «неотрицательными», т.е.
является «неотрицательными», т.е. ![]() при всех k=1,2,…,s.
при всех k=1,2,…,s.
Полагаем, что носители координат-векторов ![]() совпадают, т.е.
совпадают, т.е.
| |
(2) |
при всех k=1,2,…,s. Это означает, что множество вторых индексов, отличных от нуля координат следующих векторов
совпадают при всех k=1,2,…,s, при этом положим, что
| |
(2*) |
Полагается, что вектор
| |
(3) |
с координатами-векторами
| |
(4) |
является «положительным», т.е. носители векторов-координат (4)
| |
(5) |
при всех k=1,2,…,s, точнее
| |
(6) |
при всех k=1,2,…,s.
Пусть множество
| |
(7) |
является множеством всевозможных векторов ![]() с координатами
с координатами ![]() Очевидно, что количество векторов множества Q равно
Очевидно, что количество векторов множества Q равно
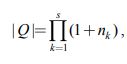 |
(8) |
следовательно
| |
(9) |
| |
(10) |
при s=1,
| |
(11) |
при s=n.
Заданной тройке векторов (1)-(6) ставится в соответствие (с помощью множества Q) набор новых векторов
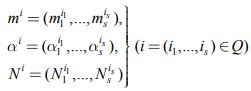 |
(12) |
с координатами-векторами
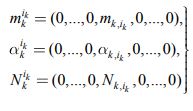 |
(13) |
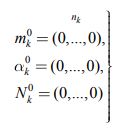 |
(14) |
Вводим полунорму
Через
как замыкание множества достаточно гладких, финитных в En функций по этой норме (32). Пространство (33), в случае s=1, является обобщением известных пространств Соболева-Слободецкого
| |
(34) |
В случае s=n пространство (33) является обобщением пространства
| |
(35) |
функций с доминирующей смешанной производной приведенного в работах С.М.Никольского, П.И.Лизоркина, А.Дж.Джабраилова и других.
Замечание 2. В случае ограничения вида
| |
(36) |
норма (30) переобозначается как
| |
(37) |
В этом случае (36) норма (37) определяет пространства
| |
(38) |
как замыкание множества достаточно гладких, финитных En в функций по этой норме (37). Пространства (38), в случае s=1, является обобщением известных пространств
| |
(39) |
С.М.Никольского-О.В.Бесова.
Пространства (38), в случае s=n, является известными пространствами
| |
(40) |
изученных в работах С.М.Никольского, А.Дж.Джабраилова, И.Т.Аманова и других.
Пусть ![]() а вектор
а вектор ![]() с координатами-векторами
с координатами-векторами
Множество ![]() называется «σ-полурогом» вершиной в точке
называется «σ-полурогом» вершиной в точке ![]() .
.
Заметим, что «σ-полурог» ![]() в случае s=1 становится «σ-рогом» с вершиной в точке
в случае s=1 становится «σ-рогом» с вершиной в точке ![]() , определенного О.В.Бесовым, а в случае s=n указанной
, определенного О.В.Бесовым, а в случае s=n указанной ![]() «σ-полурог» становится n-мерным прямоугольником с одной из вершиной в точке
«σ-полурог» становится n-мерным прямоугольником с одной из вершиной в точке ![]() , с гранями параллельных координатным осям.
, с гранями параллельных координатным осям.
При фиксированных векторов ![]() количество «σ-полурогов» с вершиной в точке
количество «σ-полурогов» с вершиной в точке ![]() , равно 2n, а если фиксировать и вектор
, равно 2n, а если фиксировать и вектор ![]() тогда имеем единственного «σ-полурога», вершиной в точке
тогда имеем единственного «σ-полурога», вершиной в точке ![]() .
.
Определение. Подобласть ![]() называется подобластью, удовлетворяющей условию «σ-полурога», если существует такой вектор
называется подобластью, удовлетворяющей условию «σ-полурога», если существует такой вектор ![]() , либо при котором
, либо при котором
| |
(42) |
Определение. Область ![]() называется областью, удовлетворяющей условию «σ-полурога», если существует конечный набор подобластей
называется областью, удовлетворяющей условию «σ-полурога», если существует конечный набор подобластей ![]() удовлетворяющих условию «σ-полурога», покрывающих область G, т.е. таких, что
удовлетворяющих условию «σ-полурога», покрывающих область G, т.е. таких, что
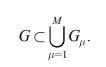 |
(43) |
Класс областей ![]() , удовлетворяющих условию «σ-полурога» обозначим через C(σ,H).
, удовлетворяющих условию «σ-полурога» обозначим через C(σ,H).
Напомним, что класс областей ![]() , удовлетворяющих условию «σ-полурога», в случае s=1, становится классом областей, удовлетворяющих условию «σ-рога», определенных О.В.Бесовым, а в случае s=n, этот класс областей
, удовлетворяющих условию «σ-полурога», в случае s=1, становится классом областей, удовлетворяющих условию «σ-рога», определенных О.В.Бесовым, а в случае s=n, этот класс областей ![]() , удовлетворяющих условию «σ-полурога», становится классом областей
, удовлетворяющих условию «σ-полурога», становится классом областей ![]() , удовлетворяющих условию «прямоугольников», рассмотренных в работах В.П.Ильина.
, удовлетворяющих условию «прямоугольников», рассмотренных в работах В.П.Ильина.
Основные результаты работы даются в виде формулировки следующую теорем (без доказательства), описывающие основные дифференциальные свойства функций f=f(x) в области ![]() , удовлетворяющей условию «σ-полурога».
, удовлетворяющей условию «σ-полурога».
Теорем. Пусть
| |
(44) |
где ![]() при этом тройка векторов
при этом тройка векторов ![]() подчинены условиям (1)-(6).
подчинены условиям (1)-(6).
Пусть область ![]() где
где ![]() а вектор
а вектор ![]() , с координатами-векторами
, с координатами-векторами ![]() является произвольным фиксированным «положительным», т.е.
является произвольным фиксированным «положительным», т.е. ![]() .
.
Пусть «целочисленный неотрицательный» ![]() вектор с координатами-векторами
вектор с координатами-векторами ![]() подчинен условиям
подчинен условиям
В условиях теоремы полагается, что область ![]() удовлетворяет условию «σ-полурога», при этом вектор
удовлетворяет условию «σ-полурога», при этом вектор ![]() с координатами-векторами
с координатами-векторами ![]() произвольный «положительный», т.е.
произвольный «положительный», т.е. ![]() -произвольные при всех
-произвольные при всех![]() .
.
Предполагая, что
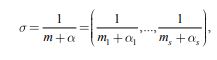 |
(48) |
с координатами-векторами
мы сужаем класс областей ![]() , т.е., в этом случае, мы говорим, что геометрия области
, т.е., в этом случае, мы говорим, что геометрия области
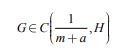 |
(49) |
соответствует показателям гладкости пространств ![]() , но именно в этом случае (48) получаются наиболее полные дифференциальные свойства функций
, но именно в этом случае (48) получаются наиболее полные дифференциальные свойства функций ![]() .
.
В предположении (49) условия (45) теоремы записываются в виде
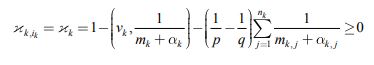 |
(50) |
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
- Максудов Ф.Г. Метод интегральных представлений в теории пространств / Ф.Г.Максудов, А.Дж.Джабраилов. Баку, изд., «Элм», 2000 г.
- Соболев С.Л. Некоторые применения функционального анализа в математической физике /С.Л.Соболев. Ленинград, изд., ЛГУ, 1950 г.
- Слободецкий С.Л. Пространства Соболева дробного порядка и их дифференциальные уравнения в частных производных / С.Л.Слободецкий. ДАН СССР, т.118, №2, 1958 г.
- Никольский С.М. Приближение функций многих переменных и теоремы вложения /С.М.Никольский. Москва, изд., «Наука», 1977 г.
- Джабраилов А.Д. О некоторых функциональных пространствах. Прямые и обратные теоремы вложения / А.Д.Джабраилов. ДАН СССР, т.159, 1964 г.
- Бесов О.В. Интегральные представления функций и теоремы вложения /О.В. Бесов, В.П. Ильин, С.М. Никольский. Москва, изд., «Наука», 1975 г.
- Лизоркин П.И. Классификация дифференциальных функций на основе пространств с доминирующей смешанной производной /П.И. Лизоркин, С.М. Никольский // Труды МИАН СССР, т.77, 1965 г.
- Аманов Т.М. Пространства дифференцируемых функций с доминирующей смешанной производной /Т.М.Аманов. Алма-Аты, изд., «Наука», 1976 г.
- Джабраилов А.Дж. К теории «теорем вложения» /А.Дж.Джабраилов // Труды МИАН СССР, т.89, 1967 г.
- Нейматов Н.А. Весовые интегральные представления и некоторые весовые теоремы вложения/Н.А.Нейматов. Баку, Защищенная диссертационная работа, НАН Азер., 2015 г.
Список литературы на английском языке / ReferencesinEnglish
- Maksudov F.G. Metod integral'nyh predstavlenij v teorii prostranstv [The method of integral representations in the theory of spaces] / F.G. Maksudov, A.J. Dzhabrailov. Baku, ed., "Elm", 2000 [in Russian]
- Sobolev S.L. Nekotorye primenenija funkcional'nogo analiza v matematicheskoj fizike [Some applications of functional analysis in mathematical physics] / S.L. Sobolev. Leningrad, ed., LSU, 1950 [in Russian]
- Slobodetsky S.L. Prostranstva Soboleva drobnogo porjadka i ih differencial'nye uravnenija v chastnyh proizvodnyh [Sobolev spaces of fractional order and their partial differential equations] / S.L. Slobodetsky. DAN USSR, vol.118, No. 2, 1958 [in Russian]
- Nikolsky S.M. Priblizhenie funkcij mnogih peremennyh i teoremy vlozhenija [Approximation of functions of many variables and embedding theorems] / S.M. Nikolsky. Moscow, ed., "Science", 1977. [in Russian]
- Dzhabrailov A.D. O nekotoryh funkcional'nyh prostranstvah. Prjamye i obratnye teoremy vlozhenija [On some functional spaces. Direct and inverse embedding theorems] /A.D. Dzhabrailov. DAN USSR, vol.159, 1964 [in Russian]
- Besov O.V. Integral'nye predstavlenija funkcij i teoremy vlozhenija [Integral representations of functions and embedding theorems] / O.V. Besov, V.P. Ilyin,S.M. Nikolsky. Moscow, ed., "Science", 1975. [in Russian]
- Lizorkin P.I. Klassifikacija differencial'nyh funkcij na osnove prostranstv s dominirujushhej smeshannoj proizvodnoj [Classification of differential functions based on spaces with a dominant mixed derivative] / P.I. Lizorkin, S.M. Nikolsky // Trudy MIAN SSSR[Proceedings of the MIAN USSR], vol. 77, 1965. [in Russian]
- Amanov T.M. Prostranstva differenciruemyh funkcij s dominirujushhej smeshannoj proizvodnoj[Spaces of differentiable functions with dominant mixed derivative] /T.M. Amanov. Alma-Ata, ed., "Science", 1976 [in Russian]
- Dzhabrailov A.J. K teorii «teorem vlozhenija» [To the theory of "embedding theorems"] / A.J. Dzhabrailov // Trudy MIAN SSSR[Proceedings of the MIAN USSR], vol.89, 1967 [in Russian]
- Neymatov N.A. Vesovye integral'nye predstavlenija i nekotorye vesovye teoremy vlozhenija [Weight integral representations and some weight embedding theorems] / N.A. Neymatov. Baku, Defended dissertation, NAS Azer., 2015 [in Russian]