КОМБИНАТОРНОЕ ЗНАЧЕНИЕ ЧИСЛА ЭЙЛЕРА
КОМБИНАТОРНОЕ ЗНАЧЕНИЕ ЧИСЛА ЭЙЛЕРА
Научная статья
Перфилеев М.С. *
ORCID: 0000-0002-9776-3666,
Восточно-Сибирский филиал ФГУП «ВНИИФТРИ», Иркутск, Россия
* Корреспондирующий автор (perfmihserg18011985[at]mail.ru)
АннотацияВ настоящей статье рассматривается новый предел числа e и приводится его научное доказательство с помощью аппарата математического анализа. Используя этот предел, мы проводим комбинаторную интерпретацию числа Эйлера. Это означает, что число Эйлера является отношением количества перестановок (или комбинаций) ![]() на n к числу перестановок (или комбинаций)
на n к числу перестановок (или комбинаций) ![]() на n с бесконечно большим числом элементов n.
на n с бесконечно большим числом элементов n.
Ключевые слова: число Эйлера, предел функции, формула Стирлинга, число перестановок, количество комбинаций.
COMBINATORIAL MEANING OF EULER'S NUMBER
Research article
Perfileev M.S. *
ORCID: 0000-0002-9776-3666,
East-Siberian branch of FSUE «VNIIFTRI», Irkutsk, Russia
* Corresponding author (perfmihserg18011985[at]mail.ru)
AbstractIn this paper, we consider a new limit for the number e and give its rigorous proof using the apparatus of mathematical analysis. With the help of this limit, a combinatorial interpretation is given for Euler's number. It means that Euler's number is the ratio of the number of permutations (or combinations) of ![]() by n to the number of permutations (or combinations) of
by n to the number of permutations (or combinations) of ![]() by n with an infinitely large number of elements n.
by n with an infinitely large number of elements n.
Keywords: Euler's number, limit of a function, Stirling's formula, number of permutations, number of combinations.
IntroductionThe number e is one of the most important mathematical constants [1], and it plays a huge role in differential and integral calculus, in algebra and the laws of physics and chemistry. Euler's number has various representations, for example, sums of infinite series, limits, infinite multiplications, and infinite continued fractions [2], [3].
Let's consider the limit
![]() (1)
(1)
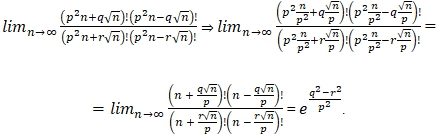 We denote that
We denote that 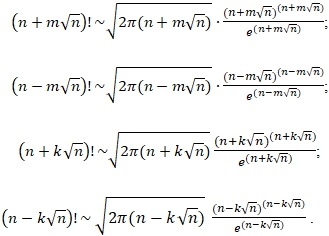
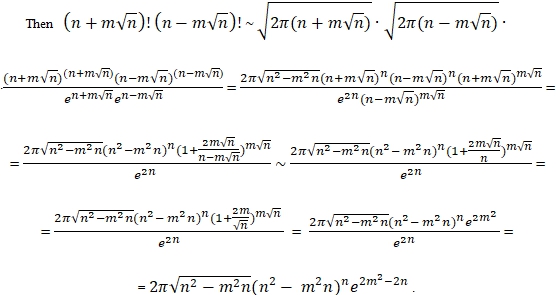
(Note: during the transformations, we used the negligible smallness of ![]() compared to n provided
compared to n provided ![]() and the second remarkable limit
and the second remarkable limit ![]() [6]).
[6]).
Similarly, we can get
![]()
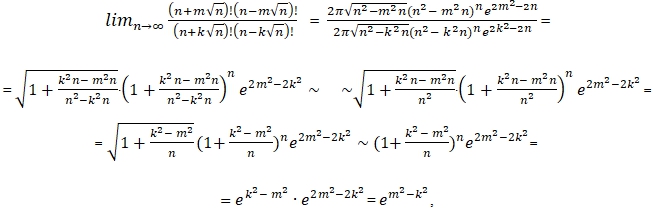
Q.E.D.
(Note: during the transformations, we used the negligible smallness of ![]() compared to
compared to ![]() provided
provided ![]() and the second remarkable limit).
and the second remarkable limit).
Combinatorial meaning of Euler's number
Let's consider some properties of the obtained limit (1).
If we take p = 1, and ![]() (Theodorus' constant), and
(Theodorus' constant), and ![]() (Pythagoras' constant) [1], then we get the limit
(Pythagoras' constant) [1], then we get the limit
![]() (3)
(3)
Using highly accurate computer calculations for the expression (5), we can get the following results, presented in this format:
{numeric value n ; deviation of calculated results from the exact value of the number e}:
![]()
It is easy to see that as n increases by one order of magnitude, the accuracy of the approximation increases by two orders of magnitude.
Using the formula for the number of permutations of k elements of m elements,
![]() [7] can be trivially obtained
[7] can be trivially obtained
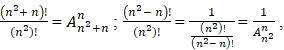 (6)
(6)
Thus, Euler's number also has a combinatorial meaning, which is the ratio of the number of permutations of n elements from ![]() elements to the number of permutations of n elements from
elements to the number of permutations of n elements from ![]() elements with an infinitely large number of elements n.
elements with an infinitely large number of elements n.
Also, Euler's number can be interpreted as the ratio of the number of combinations of n elements from ![]() elements to the number of combinations of n elements from
elements to the number of combinations of n elements from ![]() elements with an infinitely large number of elements n.
elements with an infinitely large number of elements n.
Indeed, using the formula for the number of combinations
![]()
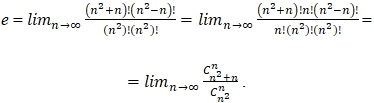 (9)
If in the limit (5) we replace n with
(9)
If in the limit (5) we replace n with 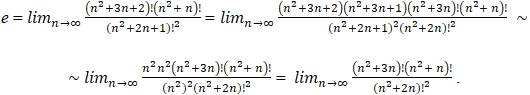 (10)
(10)
(Note: during the transformations, we used the negligible smallness of compared to ![]() provided
provided ![]() ).
).
Conclusion
Thus, this paper presents and proves a new limit for Euler's number. The properties of this limit have also been considered here. Using the formulas for the number of permutations and combinations of m through k, it is shown that the number e has its combinatorial meaning.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Булыко А.Н. Современный словарь иностранных слов / Булыко А.Н. – М.: Мартин, 2005. – С. 215
- Steven R. Finch. Mathematical Constants / Steven R. Cambridge, 2003.- P. 12-16.
- Representations of e [Electronic resourse]. URL: https://www.wolframalpha.com/input/?i=Representations+of+e (accessed: 18.07.2019)
- Wolfram MathWorld [Electronic resourse]. URL: http://mathworld.wolfram.com/e.html (accessed: 18.07.2019)
- Colloquium-journal, Warszawa, Poland, №4 (28), Michael Perfileev "The quotient of the number pi and the number e".- P. 60-62.
- David H. Bailey Pi: The Next Generation: A Sourcebook on the Recent History of Pi and Its Computation / David H. Bailey, Jonathan M. Borwein.-Springer, 2016.- 389 p.
- Taktarov N.G. Handbook of higher mathematics for students / Taktarov N.G. Moscow, Librocom, 2008.- 149 p.
- Novikov F.A. Discrete mathematics for programmers / Novikov F.A. St. Petersburg, Piter, 2009.- P. 181-182.
- Erosh I.L. Discrete Math. Combinatorics: Tutorial / Erosh I.L. St. Petersburg, SPbGUAP, 2001.-11 p.
