ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ СТРУКТУРЫ СВЕРХЗВУКОВОЙ СТРУИ В ДВУМЕРНОМ СОПЛЕ В ЗАВИСИМОСТИ ОТ ПОКАЗАТЕЛЯ АДИАБАТЫ
ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ СТРУКТУРЫ СВЕРХЗВУКОВОЙ СТРУИ В ДВУМЕРНОМ СОПЛЕ В ЗАВИСИМОСТИ ОТ ПОКАЗАТЕЛЯ АДИАБАТЫ
Научная статья
Гвоздева Л.Г.1, *, Чулюнин А.Ю.2
1 Федеральное государственное бюджетное учреждение науки Объединенный институт высоких температур РАН (ОИВТ РАН), Москва, Россия;
2 Научно-исследовательский институт механики МГУ им. М. В. Ломоносова, Москва, Россия
* Корреспондирующий автор (chulyu-n[at]mail.ru)
АннотацияВ работе на базе численного моделирования проводится исследование структуры сверхзвуковой струи, истекающей из плоского сопла [8]. Проведено методическое исследование по оценке влияния моделей турбулентности на структуру потока. Результаты сопоставлены с экспериментальными данными. Показано, что при изменении параметра NPR может наблюдаться как маховское так и регулярное отражение. Выявлено, что изменение показателя адиабаты γ может привести к смещению точки отрыва внутри сопла.
Ключевые слова: сверхзвуковая струя, численное моделирование, турбулентные течения, маховское отражение, регулярное отражение.
NUMERICAL STUDY OF SUPER-SOUND JET STRUCTURE IN TWO-DIMENSIONAL NOZZLE DEPENDING ON ADIABAT INDICATOR
Research article
Gvozdeva L.G.1, *, Chulyunin A.Yu.2
1 Federal State Budgetary Institution of Science Joint Institute for High Temperatures of the Russian Academy of Sciences (JIHT RAS), Moscow, Russia;
2 Research Institute of Mechanics, Lomonosov Moscow State University, Moscow, Russia
* Corresponding author (chulyu-n[at]mail.ru)
AbstractBased on the numerical simulation, the structure of a supersonic jet flowing from a flat nozzle is studied in work [8]. A methodical study is conducted in order to assess the influence of turbulence models on the flow structure. The results are compared with experimental data. It is shown that when the NPR parameter is changed, both Mach and regular reflection can be observed. It is revealed that a change in the adiabatic index γ can lead to a displacement of the separation point inside the nozzle.
Keywords: supersonic jet, numerical simulation, turbulent flows, Mach reflection, regular reflection.
Исследование маховского и регулярного отражений, а также процессов перехода между этими двумя состояниями является фундаментальной научной проблемой и на протяжении десятков лет привлекает внимание ученых со всего мира. Как правило, исследования в данном направлении базируются на решении задачи об обтекании двух тел, разделённых плоскостью симметрии (например, клиньев). В последние 5 лет авторами были проведены аналитические [1] и численные исследования [2], показавшие наличие нового типа конфигурации - маховского отражения с отрицательным углом, построены границы существования режимов. Подобные результаты получены также в работе Шоева и Иванова, в котором исследуется тандем клиньев и плоской задней частью [3].
Изучение подобных трехударных конфигураций особенно важно при исследовании сверхзвуковых струй, истекающих из сопел, поскольку форма струи напрямую влияет на аэродинамические характеристики летающего аппарата. В работе [4] показано наличие гистерезиса в структуре сверхзвуковой струи, при переходе из маховского в регулярное отражение, в зависимости от параметра JPR - отношения давления в струе к давлению в окружающем пространстве. Исследования других научных групп [5] были направлены на изучение структуры течения внутри сопла, в зависимости от NPR (Nozzle Pressure Ratio) - отношения давление на входе в сопло к давлению в окружающем пространстве. Обнаружено, что при низких значениях NPR внутри сопла образуется возвратное течение.
Следует отметить, что в подавляющем большинстве случаев и расчетные и экспериментальные работы по данной тематике проводятся для воздуха, имеющего показатель адиабаты 1.4, вместе с тем, в реальных условиях приходится иметь дело с газами, имеющими меньшее значение γ. В связи с этим авторами ранее были проведены аналитические [6] и численные исследования [7] по оценке влияния гамма на структуру сверхзвуковой струи. В настоящей работе, являющейся продолжением [7], представлены результаты численного моделирования сопла, имеющего реальный прототип и для которого получены экспериментальные результаты [8].
Компьютерная модель
Для описания процесса истечения сверхзвуковой струи из сопла используется система сжимаемых, осредненных по Рейнольдсу уравнений Навье-Стокса (RANS), в совокупности с уравнением энергии. В тензорной форме эти уравнения имеют следующий вид:
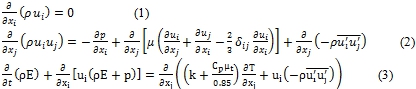
В приведенных уравнениях используются следующие обозначения: ρ – плотность рабочей среды, кг/м3; u – скорость рабочей среды, м/с; p – давление, Па; µ - коэффициент динамической вязкости, Па·с; δ – символ Кронекера; E – удельная энергия, Дж/кг; T – температура газа, К, Cp – теплоемкость при постоянном давлении, Дж/кг·К; µt – коэффициент турбулентной вязкости, Па·с. ![]() - напряжения Рейнольдса.
- напряжения Рейнольдса.
Для того, чтобы замкнуть систему (1)-(3) необходимо определить выражение для напряжений Рейнольдса, а также для давления. Для вычисления давления применяется закон идеального газа: ![]() . Определение рейнольдсовых напряжений осуществляется с помощью дифференциальных моделей турбулентности. В настоящей работе используются двухпараметрические модели SST [9] и k-ε realizable [10], а также однопараметрическая модель Spalart-Allmares [11].
. Определение рейнольдсовых напряжений осуществляется с помощью дифференциальных моделей турбулентности. В настоящей работе используются двухпараметрические модели SST [9] и k-ε realizable [10], а также однопараметрическая модель Spalart-Allmares [11].
В качестве объекта исследования рассматривается плоское сопло из работы [10], схема которого представлена на Рис.1. Координаты характерных точек сопла, необходимые для его построения, представлены в Таблице 1.
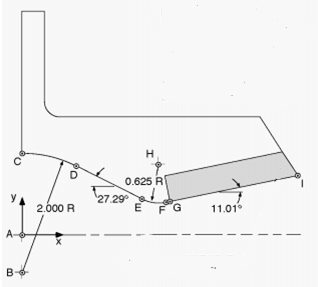
Рис. 1 – Чертеж рассматриваемого сопла [8]
Таблица 1 – Координаты опорных точек рассматриваемого сопла
| Точка | Координаты, дюйм | |
| X | Y | |
| A | 0 | 0 |
| B | 0 | -0.614 |
| C | 0 | 1.386 |
| D | 0.917 | 1.163 |
| E | 1.988 | 0.611 |
| F | 2.394 | 0.553 |
| G | 2.430 | 0.559 |
| H | 2.275 | 1.166 |
| I | 4.55 | 0.972 |
В работе, для решения системы уравнений (1)-(3) используется метод контрольного объема. Для дискретизации расчетной области на элементы используется неструктурированная сетка многогранного типа (polyhedral mesh). Сетка строится таким образом, что внутри сопла и его следе сетка достаточно мелкая. Размер ячейки выбирается таким образом, чтобы на горловину сопла приходилось минимум 150 элементов. При удалении от интересующей зоны сетка постепенно разряжается. Также необходимо отметить, что при решении задачи, описываемой в рамках RANS-подхода необходимо качественное разрешение пристеночной зоны, ячейки в этой области должны быть правильной формы и, желательно, размера. Для обеспечения этих требований используется призматический слой ячеек. Размер первой ячейки выбран таким образом, чтобы параметр y+<5, это позволяет обойти необходимость дополнительного использования механизма пристеночных функций. На Рис.2 а, б, представлена используемая расчетная область, а также фрагмент сеточной модели.
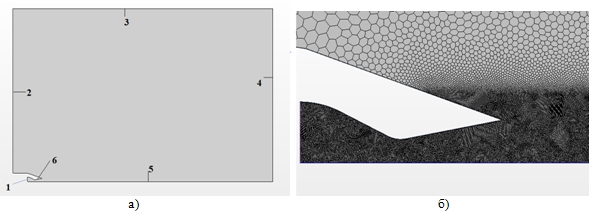
Рис. 2 – Модель сопла. а) Геометрическая модель расчетной области, б) Фрагмент сеточной модели
Граничные условия, используемые для решения задачи, представлены в Таблице 2. Индексация границ происходит в соответствии с Рис.2а.
Таблица 2 – Граничные условия
| Номер границы | Тип условия |
| 1 | Полное давление, Pt. Величина переменная Полная температура, Tt = 300 К |
| 2,3 | Полное давление, Pt = 101325 Па Полная температура, Tt = 300 К |
| 4 | «Мягкие» граничные условия для скорости, давления и температуры. Значения на границу передаются путем экстраполяции с соседних ячеек |
| 5 | Условие симметрии |
| 6 | Адиабатическая стенка. Условие прилипания для скорости =0. И равенство нулю теплового потока на стенке q=0 |
Валидация
При численном моделировании задач механики жидкости и газа, перед проведением серии расчетов, всегда следует обращать внимание на вопросы валидации и верификации получаемого решения. Валидация возможна в случае, когда для рассматриваемого объекта существуют экспериментальные данные, на которые можно опереться при выборе различных параметров (модели турбулентности, шага расчетной сетки, схемных параметров и т.д). В данной работе мы используем процедуру валидации для определения модели турбулентности, которая наилучшим образом описывает структуру течения внутри диффузора. Сравнение проводится при значении показателя адиабаты γ = 1.4.
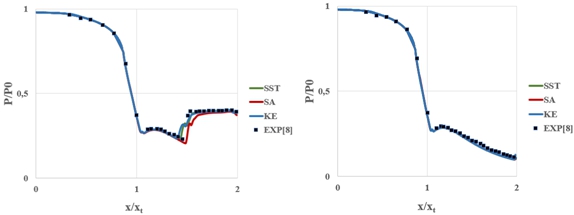
На Рис.3а, б, представлены результаты сравнения распределения безразмерного давления по профилю диффузора трех моделей турбулентности – SST, k-ε realizable и SA c экспериментальными данными при значениях NPR=2.412 и 5.423. Для обезразмеривания давления используется давление на входе в сопло – P0. По оси абсцисс отложена безразмерная координата x/xt, где xt – координата горловины сопла.
Рис. 3 – Распределение безразмерного давления по поверхности сопла. а) NPR=2.412, б) NPR=5.423
Анализ полученных графиков показывает, что при высоких значениях NPR все рассмотренные модели турбулентности ведут себя одинаково и показывают хорошее согласование с экспериментальными данными. При NPR=2.412, когда внутри сопла формируется отрывное течение модели турбулентности начинают вести себя по-разному в зоне отрыва, сохраняя хорошее совпадение до этого места. Модель Spalart-Allmares (SA) предсказывает смещение точки отрыва ближе к выходному сечению сопла. Модель k-ε realizable предсказывает чуть большее смещение к горловине сопла. Наилучшие результаты продемонстрировала модель SST, которая и будет использована в дальнейшем для оценки влияния показателя адиабаты γ на структуру сверхзвуковой струи.
Результаты моделирования
На Рис. 4.а-г представлены поля чисел Маха, полученные при различных значениях параметра NPR и γ=1.4. Картины свидетельствуют, что наблюдается принципиально разное поведение потока. Так, при NPR ≥5.423 и выше наблюдается типичная для перерасширенной сверхзвуковой струи конфигурация с многократным взаимодействием волн сжатия и разряжения в следе за соплом.
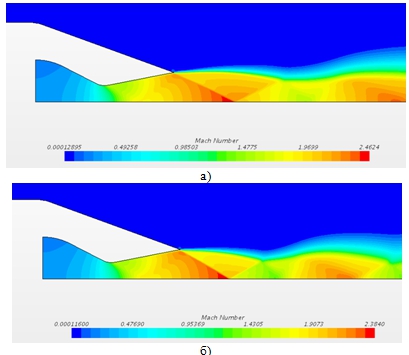
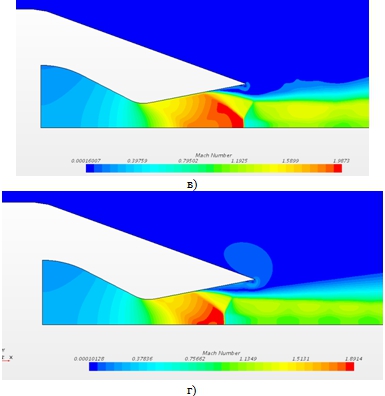
Рис. 4 – Поля чисел Маха, полученный при γ=1.4. а) NPR=7.04, б) NPR=5.423, в) NPR=3.014, г) NPR=2.412
При уменьшении NPR до 3.014 структура струи разрушается, начинает трехударная маховская конфигурация, состоящая из нормальной волны в ядре сопла и косой ударной волны, отходящей от его стенок. Для данной конфигурации характерным является формирование дозвуковой зоны за ножкой Маха. При этом естественно формирование отрыва потока на стенке. Точка отрыва зависит от показателя NPR и тем ближе к выходу, чем выше его значение.
На Рис.5а, б представлено сравнение векторов скоростей, полученных при одном значении NPR=3.014, но при разных значениях показателя адиабаты (γ=1.4 и 1.1).
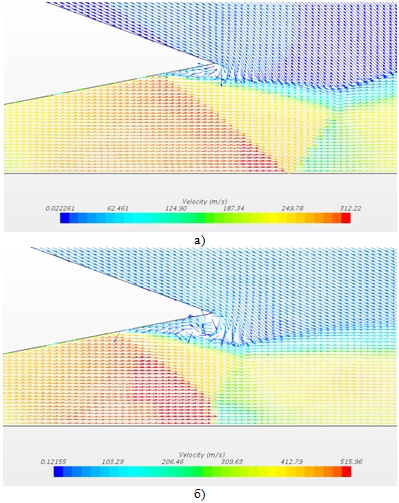
Рис. 5 – Векторное поле скоростей. NPR=3.014. a) γ=1.4, б)γ=1.1
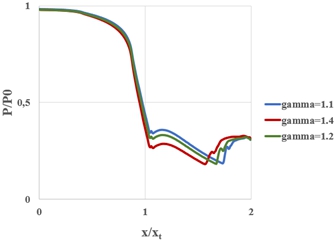
Рис. 6 – Распределение давления по поверхности сопла при различных значениях γ
Представленные поля скоростей, а также график распределения безразмерного давления по контуру сопла (Рис.6) показывает, что уменьшение NPR позволяет отодвинуть точку отрыва ближе к выходному сечению и уменьшить размер отрывной зоны. Важным является то обстоятельство, что уменьшение показателя адиабаты приводит к перестройке структуры сверхзвуковой струи: при уменьшении γ сначала уменьшается ножка маха, а затем маховское отражение переходит в регулярное (см.рис.5а, 5б).
Заключение
Проведенные в работе вычислительные эксперименты показали, что для расчета конфигурации сопла [8] наиболее целесообразно использовать модель турбулентности SST, которая дает хорошее согласование как для больших чисел NPR, при которых не наблюдается отрыв, так и для отрывных режимов с малым NPR. Показано, что на отрывных режимах, увеличение NPR приводит к смещению точки отрыва к выходному сечению.
Выявлено, что при одних и тех же значениях NPR, в зависимости от показателя адиабаты может наблюдаться как регулярное, так и маховское отражение. Увеличение показателя адиабаты приводит к смещению точки отрыва ближе к горлу сопла.
| Финансирование Работа выполнена при финансовой поддержке РФФИ (грант 16-08-01228 А). | Funding This work was supported by the Russian Foundation for Basic Research (Grant 16-08-01228 A). |
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Gvozdeva L.G. Influence of the adiabatic index on switching between different types of shock wave reflection in a steady supersonic gas flow / L.G. Gvozdeva, S.A. Gavrenkov // Technical Physics. - 2013. - Vol. 58. - № 8. – P.1238-1241. doi: 10.1134/S1063784213080148
- Gvozdeva L.G. New configuration of irregular reflection of shock waves / L.G. Gvozdeva, S.A. Gavrenkov // Progress in Flight Physics. – 2015. – Vol.7. – P.437-452. doi: 10.1051/eucass/201507437
- Shoev G.V. Numerical study of shock wave interaction in steady flows of a viscous heat-conducting gas with a low ratio of specific heats / G.V. Shoev, M.S. Ivanov // Thermophysics and Aeromechanics. - – Vol. 23. – P.343-354. doi: 10.1134/S0869864316030045
- Shimshi E. Viscous simulation of shock-reflection hysteresis in overexpanded planar nozzles / E.Shimshi, G.Ben-Dor, A. Levy // Shock Waves. – 2011. – Vol.21. – №3. – P.205-214. doi: 10.1007/s00193-011-0325-z
- Hadjadj A. Numerical Investigation of Shock-Reflection Phenomena in Overexpanded Supersonic Jets / A.Hadjadj, A.N. Kudryvtsev, M.S. Ivanov // AIAA Journal. – 2004. - Vol. 42. - №3. – P. 570-577. doi:10.2514/1.989
- Слободкина Ф.А. Исследование трехударной конфигурации с отрицательным углом отражения в стационарном сверхзвуковом потоке / Ф.А. Слободкина, Л.Г. Гвоздева // Двигатель. – 2016. №.1(106). – С.2-5.
- Гвоздева Л.Г. Исследование зависимости структуры течения в перерасширенных сверхзвуковых соплах от показателя адиабаты / Л.Г. Гвоздева, А.Ю. Чулюнин // Междунар. науч.-исслед. журн. – 2017. – №.12-5(66). с.13-17. DOI:https://doi.org/10.23670/IRJ.2017.66.158
- Hunter C.A. Experimental, Theoretical and Computational Investigation of Separated Nozzle Flows / C.A. Hunter // AIAA Paper 98-3107. - 1998.
- Menter F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications / F.R. Menter // AIAA Journal. – 1994. -Vol.32(8). P.1598–160 doi:10.2514/3.12149
- Shih T.H. New k-ε eddy viscosity model for high Reynolds number turbulent flows – model development and validation / T.H. Shih, W. Liou, A. Shabbir, Z. Yang, J. Zhu //Computers Fluids. – 1995. – Vol. 24. – P.227-238. doi: https://doi.org/10.1016/0045-7930(94)00032-T
- Spalart, P. R. A One-Equation Turbulence Model for Aerodynamic Flows / P.R. Spalart, S.R. Allmares // AIAA Paper 92-0439. – 1993. doi: https://doi.org/10.2514/6.1992-439
Список литературы на английском языке / References in English
- Gvozdeva L.G. Influence of the adiabatic index on switching between different types of shock wave reflection in a steady supersonic gas flow / L.G. Gvozdeva, S.A. Gavrenkov // Technical Physics. - 2013. - Vol. 58. - № 8. – P.1238-1241. doi: 10.1134/S1063784213080148
- Gvozdeva L.G. New configuration of irregular reflection of shock waves / L.G. Gvozdeva, S.A. Gavrenkov // Progress in Flight Physics. – 2015. – Vol.7. – P.437-452. doi: 10.1051/eucass/201507437
- Shoev G.V. Numerical study of shock wave interaction in steady flows of a viscous heat-conducting gas with a low ratio of specific heats / G.V. Shoev, M.S. Ivanov // Thermophysics and Aeromechanics. - – Vol. 23. – P.343-354. doi: 10.1134/S0869864316030045
- Shimshi E. Viscous simulation of shock-reflection hysteresis in overexpanded planar nozzles / E.Shimshi, G.Ben-Dor, A. Levy // Shock Waves. – 2011. – Vol.21. – №3. – P.205-214. doi: 10.1007/s00193-011-0325-z
- Hadjadj A. Numerical Investigation of Shock-Reflection Phenomena in Overexpanded Supersonic Jets / A.Hadjadj, A.N. Kudryvtsev, M.S. Ivanov // AIAA Journal. – 2004. - Vol. 42. - №3. – P. 570-577. doi:10.2514/1.989
- Slobodkina F.A. Issledovanie trekhudarnoj konfiguracii s otritsatel’nym uglom otrajenija v statsionarnom sverhzvukovom potoke [Investigation of triple-shock configuration with a negative reflection angle in a steady supersonic flow] / F.A. Slobodkina, L.G. Gvozdeva // Dvigatel’.[Engine] – 2016. №.1(106). – P.2-5. [In Russian]
- Gvozdeva L.G. Issledovanie zavisimosti structury techenija v pererasschirennyh sverhzvukovykh soplah ot pokazatelya adiabaty. [Investigation of the dependence of the flow structure in overexpanded supersonic nozzles on the adiabatic index] / L.G. Gvozdeva, A.Yu. Chulyunin // Mezhdunarodnij nauchno-issledovatelskiy zhurnal.[International Research Journal]– 2017. – №.12-5(66). P.13-17. DOI: https://doi.org/10.23670/IRJ.2017.66.158 [In Russian]
- Hunter C.A. Experimental, Theoretical and Computational Investigation of Separated Nozzle Flows / C.A. Hunter // AIAA Paper 98-3107. - 1998.
- Menter F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications / F.R. Menter // AIAA Journal. – 1994. -Vol.32(8). P.1598–160 doi:10.2514/3.12149
- Shih T.H. New k-ε eddy viscosity model for high Reynolds number turbulent flows – model development and validation / T.H. Shih, W. Liou, A. Shabbir, Z. Yang, J. Zhu //Computers Fluids. – 1995. – Vol. 24. – P.227-238. doi: https://doi.org/10.1016/0045-7930(94)00032-T
- Spalart, P. R. A One-Equation Turbulence Model for Aerodynamic Flows / P.R. Spalart, S.R. Allmares // AIAA Paper 92-0439. – 1993. doi: https://doi.org/10.2514/6.1992-439